Discretization of the problem domain (Дискретизация проблемной области)

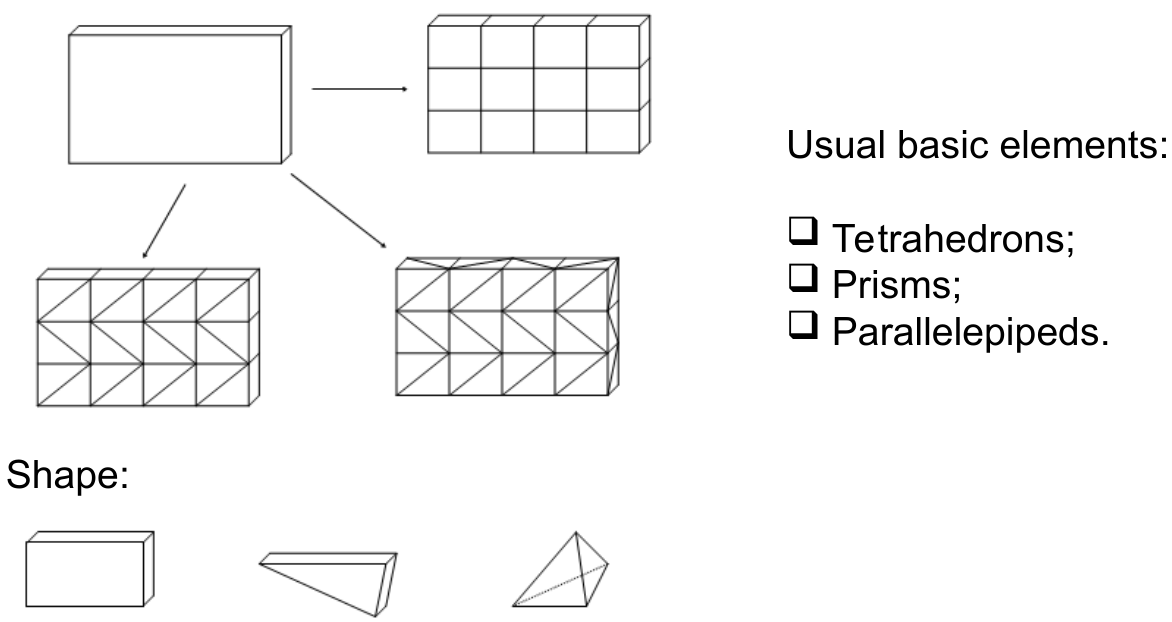
Мы должны разделить кирпич на основные элементы (тетраэдры, призмы или параллелепипеды)

Algebraic equation system (Алгебраическая система уравнений)

• Намагниченность каждого элемента считается постоянной (самый простой подход). Более сложные схемы аппроксимации не используются.

• Для формирования системы уравнений используется метод коллокаций (мы должны выбрать некоторую центральную точку внутри элемента, и магнитное поле, индуцируемое всеми частями магнитной системы, вычисляется только для этой центральной точки. И затем предполагается, что везде внутри элемента напряженность магнитного поля имеет одинаковое значение)

29. Finite element method (Метод конечных элементов)

Основные этапы:

1. Постановка задачи – область задачи, уравнение, граничные условия, свойства материала.

2. Дискретизация проблемной области.

3. Аппроксимация неизвестной функции.

4. Аппроксимация решаемого уравнения и граничных условий.

5. Решение системы алгебраических уравнений (в общем случае – нелинейных).

6. Постобработка.

Discretization (Дискретизация)

Выбор типа элемента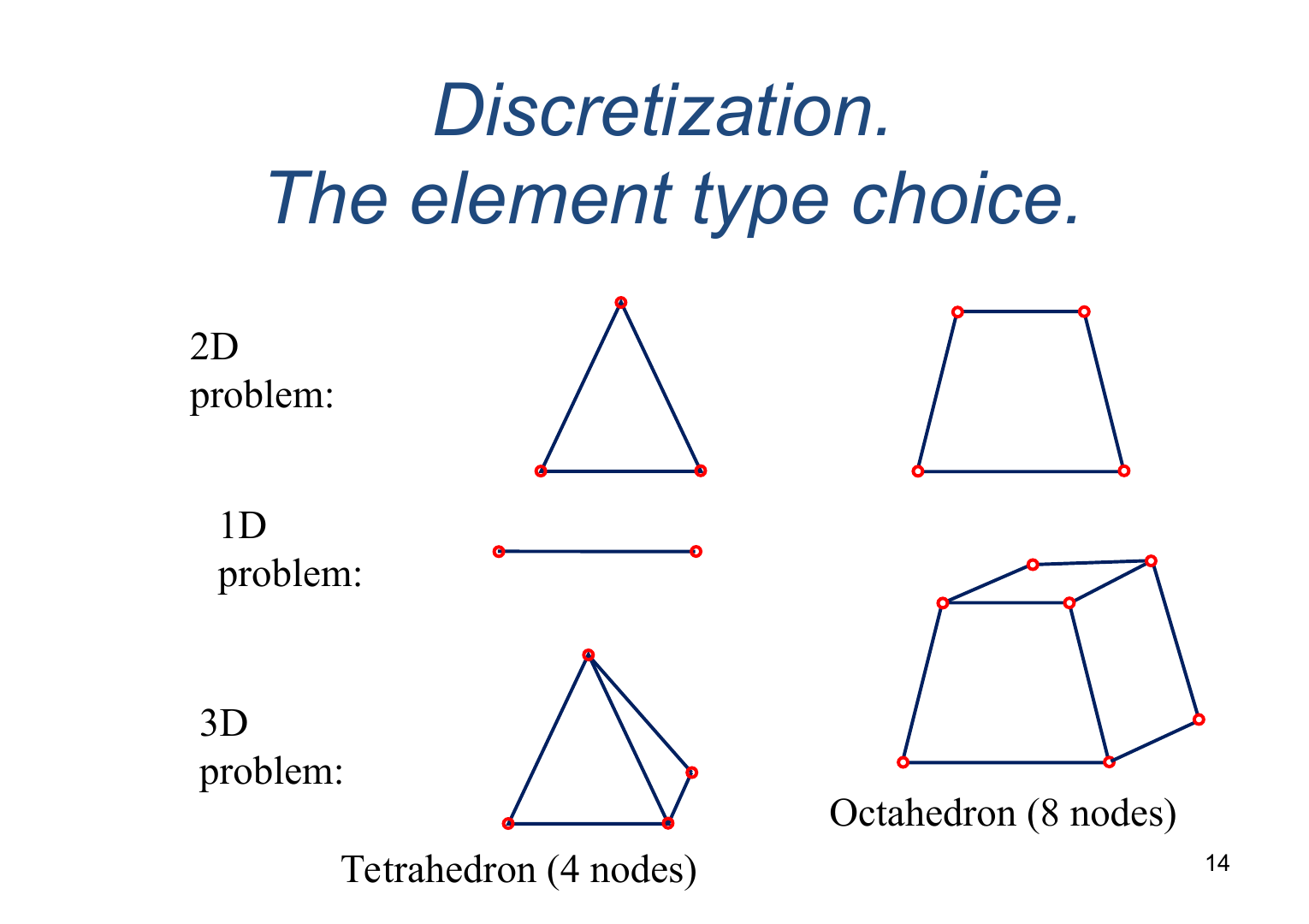

Node – узел (точка, вершина)

Примеры сетки (треугольники и четырехугольники)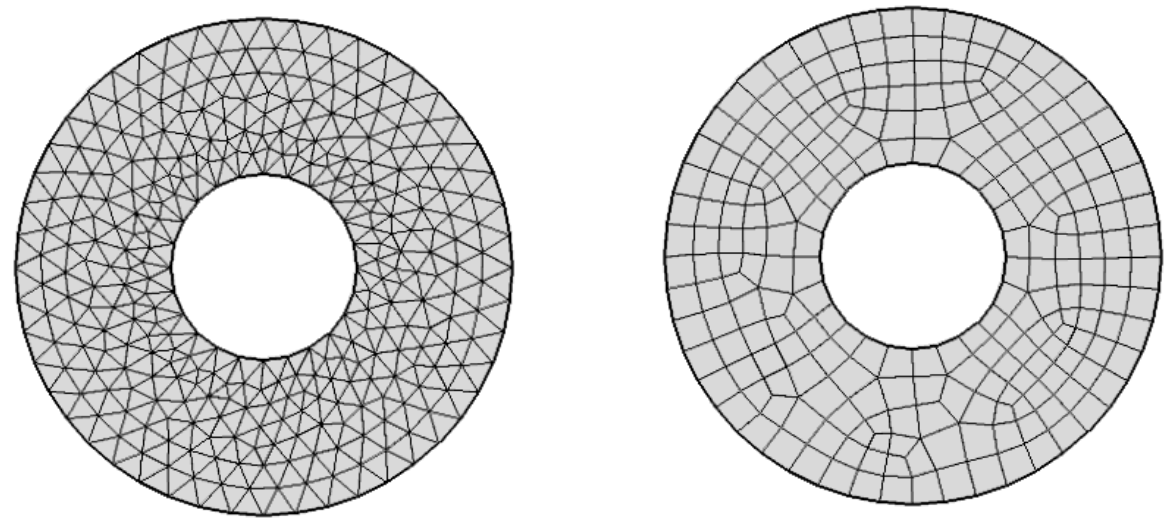

Линейная аппроксимация

Количество свободных параметров остается прежним!

В принципе, мы можем выразить коэффициенты a, b, c в терминах узловых потенциалов U₁, U₂, U₃

В линейном приближении вершины совпадают с узловыми.

30. Finite functions (Ограниченная функция – отлична от нуля только в пределах треугольника)

Конечная функция внутри треугольника может иметь разные зависимости. Все зависит от величины узлового потенциала.

Существуют три совершенно особые конечные функции:

• Конечная функция, связанная с первым узлом:

Аналогичные соотношения справедливы для 2 других конечных функций.

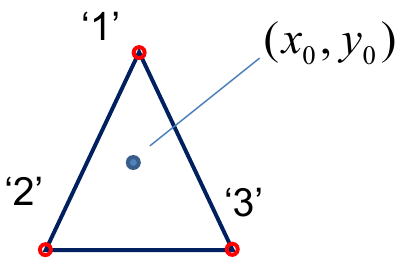
Конечные функции для треугольников = симплексные координаты (координаты – потому что каждая точка внутри треугольника может быть описана определенным значением конечных функций, поэтому поведение этих функций аналогично координатам).

Simplex coordinates

Двумерные симплексные координаты:

Другим определением положения точки является набор симплексных координат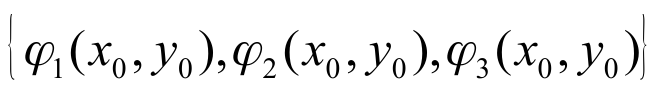

На самом деле только 2 из 3 симплексных координат независимы:

Общее соотношение для симплексных координат:

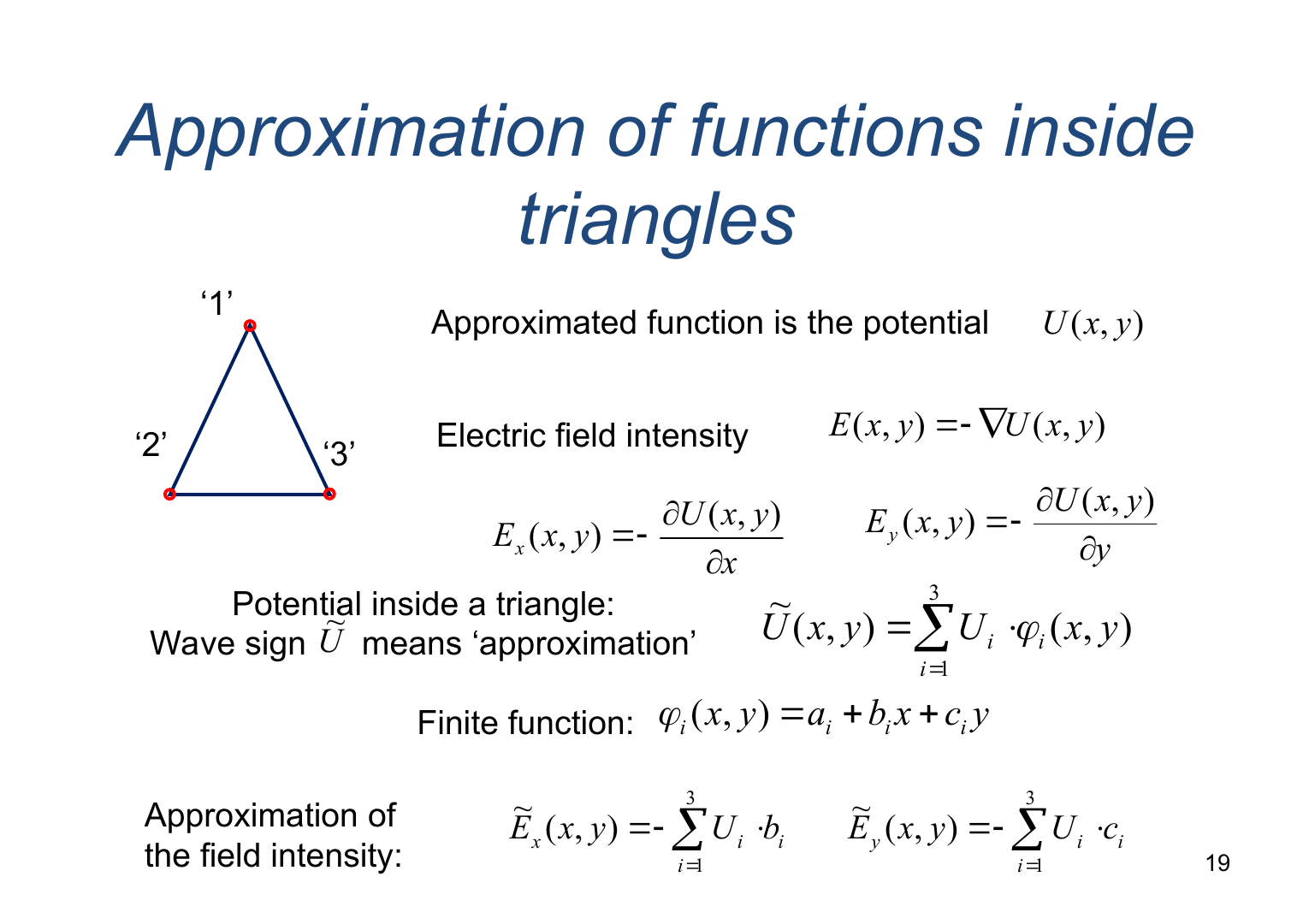
Approximation of functions inside triangles (Аппроксимация функций внутри треугольника)

Аппроксимируемая функция - это потенциальная: U(x, y)

Напряженность электрического поля

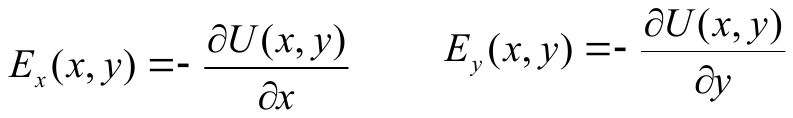
Потенциал внутри треугольника (знак волны 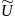означает ‘Апроксимацию’):

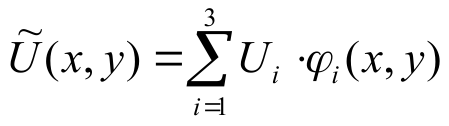
Конечная функция:

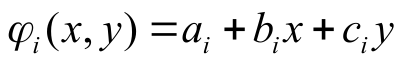
Аппроксимация напряженности поля:

Approximation of the equation (Аппроксимация уравнения)

Потенциал внутри треугольника (знак волны означает ‘Апроксимацию’):

Конечная функция:

Уравнение:

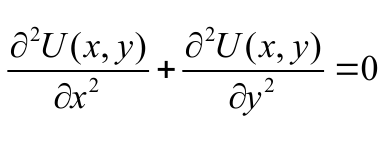
Если мы подставим аппроксимацию потенциала в это уравнение, мы полностью потеряем информацию, потому что

31. Weighted residual method (метод взвешенных невязок)

Этот метод используется для решения различных задач, и идея, лежащая в основе этого метода, нетривиальна. Давайте обратимся к исходному уравнению:

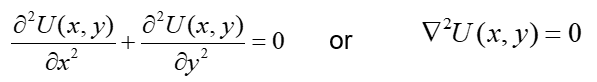
Давайте выберем некоторую произвольную функцию ψ (x, y) (мы можем выбрать некоторую произвольную функцию, которую в будущем мы будем называть взвешенной функцией). Очевидно, что если правое исходное уравнение равно нулю, то произведение этого оператора Лапласа и весовой функции будет равно нулю.

Теперь давайте интегрируем это произведение по области s (это s соответствует всей проблемной области)

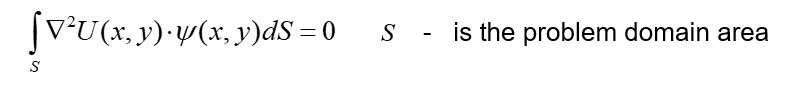
Также необходимо помнить, что мы говорим о методе конечных элементов и всех конечных функциях, и, следовательно, эти взвешенные функции также будут ограничены определенным элементом, они будут равны нулю вне рассматриваемого элемента и будут отличны от нуля внутри них. Вот почему на первый взгляд (взгляд) этот интеграл очень сложен, его следует интегрировать по широкой области, но на практике он всегда должен интегрироваться в очень маленькой области, которая ограничена рассматриваемыми элементами.

В зависимости от выбора весовых функций существуют различные методы взвешенных невязок, однако, наш выбор – метод Галеркина.

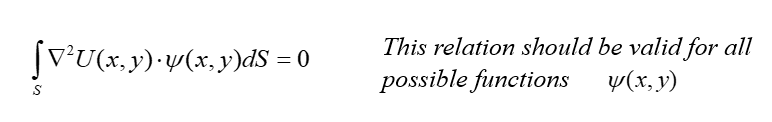
Это исходное уравнение, и это верно только потому, что лапласиан потенциала равен нулю. Очевидно, что лапласиан такого приближения не обязательно будет равен нулю, он может отличаться от нуля, поэтому интеграл от произведения весовой функции Лапласа и после интегрирования даст нам так называемый ‘взвешенный остаток’ – R:

Итак, идея метода Галеркина – это особый выбор весовых функций:

• для использования метода взвешенных остатков;

• использовать аппроксимационные функции для взвешивания:

• чтобы установить остатки равными нулю; R_j=0

применить процедуру интегрирования по частям к интегралу (слабая формулировка)

Давайте предположим, что весовая функция совпадает с конечной функцией, которая соответствует только этому треугольнику, конечно, существуют три разные функции, поэтому для каждого треугольника мы должны использовать три весовые функции. Второе предположение, установить остатки равными нулю, очевидно, мы можем выбрать аппроксимацию потенциала таким образом, чтобы остаток действительно был равен нулю, не потому, что лапласиан потенциала равен нулю, а потому, что произведение этого потенциала и весовой функции после интегрирования даст ноль. А теперь давайте применим процедуру интегрирования по частям к интегралу.

Действительно, если мы непосредственно вычислим этот интеграл, используя аппроксимацию потенциала, мы можем получить точный ноль (ноль будет равен нулю), поэтому, чтобы избежать этой трудности, можно использовать некоторое математическое преобразование, которое называется интегрированием по частям. Очень важная часть метода Галеркина заключается в том, что прямолинейное вычисление интеграла такого вида даст нам нулевой ответ только потому, что вторая производная от полинома первого порядка всегда равна нулю, и таким образом мы не сможем найти решение. Для того, чтобы преодолеть эту сложность в методе Галеркина предполагается провести идентичное преобразование – интегрирование по частям.