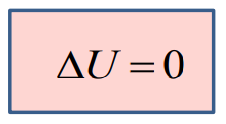- •1. Electrostatic field. Coulomb’s law. Gauss law (Электростатическое поле. Закон Кулона. Закон Гаусса)
- •Variables and units
- •Закон Кулона
- •Напряжённость электрического поля
- •Закон Гаусса
- •2. Poisson’s and Laplace’s equations for the potential of electric field (Уравнения Пуассона и Лапласа для потенциала электрического поля) Electric Potential. (Электрический потенциал)
- •Уравнения Пуассона и Лапласа
- •3. Electrostatic Energy (Электростатическая энергия)
- •Virtual experiment. (Эксперимент по нахождению энергии системы)
- •Следствия
- •4. Power and Joule’s Law (Энергия и закон Джоуля-Ленца)
- •5. Continuity Equation (Уравнения непрерывности)
- •6. Electric field induced by the charged wire placed above the flat boundary between two different dielectrics.
- •Image method for the flat boundary between magnetic media (Метод изображений для плоской границы между магнитными носителями)
- •8. Static magnetic field. Biot–Savart’s Law. Ampere’s Law (Статическое магнитное поле. Закон Био–Савара. Закон Ампера)
- •Variables and units (Переменные и единицы измерения)
- •Main Relations (Основные соотношения)
- •Magnetic flux density (Индукция магнитного поля)
- •Закон Био-Савара
- •Ampere’s law (Закон полного тока)
- •Разрез в пространстве
- •Laplace equation for the scalar magnetic potential (Уравнение Лапласа для скалярного магнитного потенциала)
- •10. Vector magnetic potential. Inductance (Векторный магнитный потенциал. Индуктивность)
- •Vector magnetic potential (Векторный магнитный потенциал)
- •Magnetic flux (Магнитный поток)
- •Differential equation for the vector magnetic potential (Дифференциальное уравнение для векторного магнитного потенциала)
- •Gauging of the vector magnetic potential (Калибровка векторного магнитного потенциала)
- •Integral presentation of the vector magnetic potential (Интегральное представление векторного потенциала)
- •Индуктивность
- •Mutual inductance (Взаимная индуктивность)
- •Inductance of thin contours (Индуктивность тонких контуров)
- •12. Internal inductance of a thin conductor (Внутренняя индуктивность тонкого проводника) Flux linkage of a thin current layer (Потокосцепление тонкого слоя с током)
- •Internal inductance of a thin conductor (Внутренняя индуктивность тонкого проводника)
- •13. Inductance of a two wire transmission line (Индуктивность двухпроводной линии).
- •14. Variable separation method in a cylindrical coordinate system (Метод разделения переменных в цилиндрической системе координат).
- •Angular function (Угловая функция)
- •Radial function (Радиальная функция)
- •General solution of the Laplace’s equation in a cylindrical coordinate system (Общее решение уравнения Лапласа в цилиндрической системе координат)
- •15. The Faraday’s law (Закон электромагнитной индукции)
- •Lenz’s Law (правило Ленца)
- •Induction by a temporal change of b (Индукция за счёт временного изменения b)
- •16. Induction through the motion of a conductor (Индукция за счет движения проводника).
- •17. Induction by simultaneous temporal change of b and motion of the conductor (Индукция одновременным изменением b во времени и движением проводника).
- •18. Unipolar generator (униполярный генератор).
- •19. Hering’s paradox (Парадокс Геринга)
- •20. Diffusion of magnetic fields into conductors (Распространение электромагнитного поля в проводнике)
- •21. Periodic electromagnetic fields in conductors. (Периодическое электромагнитное поле в проводниках)
- •Penetration of the electromagnetic field into a conductor. (Проникновение электромагнитного поля в проводник)
- •The skin effect. (Скин-эффект)
- •22. Poynting theorem. (Теорема Пойнтинга) Electromagnetic Field Energy. (Энергия электромагнитного поля)
- •The rate of decrease of the electromagnetic field energy in a closed volume. (Скорость уменьшения энергии электромагнитного поля в замкнутом объёме)
- •Transmission of energy in a dc line (Передача энергии в линиях постоянного тока)
- •The field picture near the wires with current (Картина поля вблизи провода с током)
- •25. Energy flows in static electric and magnetic fields (Поток энергии в статических электрических и магнитных полях).
- •26. The reduced magnetic potential (Редуцированный магнитный потенциал). Reduced scalar magnetic potential (Редуцированный скалярный магнитный потенциал)
- •Combination of scalar magnetic potential and reduced magnetic potential (Комбинация скалярного магнитного потенциала и редуцированного магнитного потенциала)
- •27. Classification of numerical methods of the electromagnetic field modeling (Классификация численных методов моделирования электромагнитного поля). (Классификация численных методов)
- •Classification of the problems (Классификация проблем)
- •Classification of the methods (Классификация методов)
- •28. Method of moments (Метод моментов)
- •Discretization of the problem domain (Дискретизация проблемной области)
- •Algebraic equation system (Алгебраическая система уравнений)
- •29. Finite element method (Метод конечных элементов)
- •30. Finite functions (Ограниченная функция – отлична от нуля только в пределах треугольника)
- •Simplex coordinates
- •Approximation of functions inside triangles (Аппроксимация функций внутри треугольника)
- •Approximation of the equation (Аппроксимация уравнения)
- •31. Weighted residual method (метод взвешенных невязок)
- •32. Weak formulation of the electromagnetic field modeling problem (ослабленная формулировка постановки задачи моделирования электромагнитного поля)
- •33. Boundary conditions in electric and magnetic fields (Граничные условия в электрических и магнитных полях)
- •1) First type boundary conditions (Первый тип граничных условий)
- •34. Main equations of electromagnetic field in integral form. (Основные уравнения электромагнитного поля в интегральной форме)
- •35. Main equations of electromagnetic field in differential form. (Основные уравнения электромагнитного поля в дифференциальной форме)
- •36. Electric field of a point charge (Электрическое поле точечного заряда)
- •37. Electric field of a uniformly charged sphere (Электрическое поле равномерно заряженной сферы)
- •38. Flat capacitor. Field. Surface charge. Capacity. (Плоский конденсатор. Поле. Поверхностный заряд. Вместимость.)
- •39.2 Inductance of a cylindrical coil with the rectangular cross section(Индуктивность цилиндрической катушки прямоугольного сечения).
- •4 0.1 Electric field induced by charged line placed above conducting surface (Электрическое поле, создаваемое заряженной линией, помещенной над проводящей поверхностью).
26. The reduced magnetic potential (Редуцированный магнитный потенциал). Reduced scalar magnetic potential (Редуцированный скалярный магнитный потенциал)
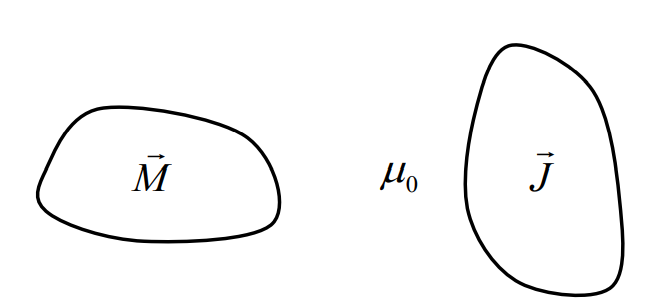
Напряженность
магнитного поля может быть представлена
в виде:
![]()
![]() это напряженность поля, индуцируемая
источниками тока
это напряженность поля, индуцируемая
источниками тока
![]()
![]() это напряженность поля, индуцируемая
намагниченными объектами
это напряженность поля, индуцируемая
намагниченными объектами
![]()
Наша проблема линейна. Это означает, что μ не зависит от величины напряженности магнитного поля, но этот принцип суперпозиции верен для любого типа магнитной системы, не имеет значения, линейна она или нет.
является потенциальным полем:
![]()
Может быть
введен особый потенциал:
![]()
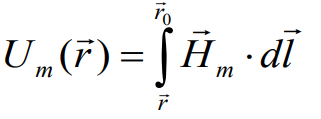
Combination of scalar magnetic potential and reduced magnetic potential (Комбинация скалярного магнитного потенциала и редуцированного магнитного потенциала)
|
|
Мы должны использовать полный магнитный скалярный потенциал внутри намагниченного объекта и везде за пределами намагниченного объекта, мы можем использовать другое представление магнитного поля.
Внутри
 -
области:
-
области:
![]() ,
U - скалярный
магнитный потенциал
,
U - скалярный
магнитный потенциал
Снаружи
- области:
![]()
Поле, индуцируемое источниками тока, может быть рассчитано по закону Био – Савара: |
|
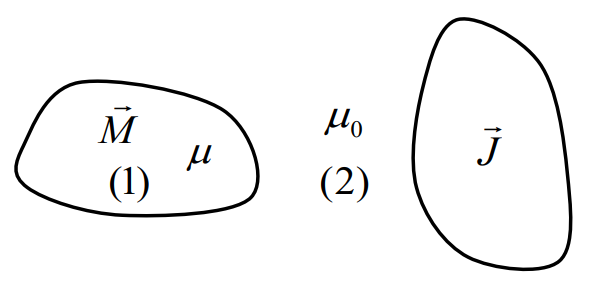
Область (1) – намагниченный объект описывается уравнением Лапласа.
Внутри намагниченной области (1) скалярный магнитный потенциал удовлетворяет дифференциальному уравнению
(1):
|
|
В (2) везде = 0 = const, вот почему потенциал удовлетворяет уравнению Лапласа.
В области (2) редуцированный магнитный потенциал удовлетворяет дифференциальному уравнению
(2):
![]() Это уравнение справедливо и в области
(1).
Это уравнение справедливо и в области
(1).
Оба уравнения одинаковы, но переменные разные
 – является границей области с намагниченным
веществом
– является границей области с намагниченным
веществом
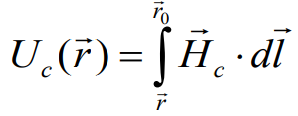 Внутри
намагниченной области:
Внутри
намагниченной области:
![]()
Скалярный магнитный потенциал токов:
Решение задачи должно обеспечивать граничные условия на
![]() (тангенциальные
компоненты магнитного поля одинаковы
по обе стороны этой границы)
(тангенциальные
компоненты магнитного поля одинаковы
по обе стороны этой границы)
 может быть рассчитан как градиент
полного магнитного потенциала внутри
1-й области.
может быть рассчитан как градиент
полного магнитного потенциала внутри
1-й области.
Мы можем рассматривать магнитное поле как суперпозицию этих двух составляющих:
![]()
или:
 ,
,
 -
редуцированный (reduced)
магнитный потенциал;
-
редуцированный (reduced)
магнитный потенциал;
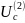 – потенциал, который индуцируется
токами (но токи не могут быть описаны
скалярным магнитным потенциалом. Мы
рассматриваем поле, которое индуцируется
токами только вдоль поверхности ,
но вдоль этой поверхности нет токов.
Вот почему в принципе мы также можем
использовать такой элемент, как скалярный
– потенциал, который индуцируется
токами (но токи не могут быть описаны
скалярным магнитным потенциалом. Мы
рассматриваем поле, которое индуцируется
токами только вдоль поверхности ,
но вдоль этой поверхности нет токов.
Вот почему в принципе мы также можем
использовать такой элемент, как скалярный
магнитный потенциал, индуцируемый токами.) Конечно, это равенство также зависит от выбора точек с нулевыми потенциалами, поэтому необходимо правильно выбирать точки с нулевыми потенциалами. В противном случае следует добавить некоторую неопределенную константу, поскольку потенциал определяется только относительно неопределенной константы.
![]()
Из условия для нормальных составляющих мы можем легко прийти к соотношению для нормальных составляющих напряженности поля.
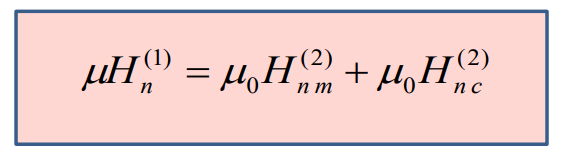
Мы можем использовать это соотношение точно для напряженности магнитного поля. Это справедливо независимо от того, как мы определили магнитные потенциалы.