17. Induction by simultaneous temporal change of b and motion of the conductor (Индукция одновременным изменением b во времени и движением проводника).

Давайте посмотрим, что произойдет, если одновременно конфигурация электромагнитного поля изменится во времени, и само магнитное поле также изменится во времени. В таком случае следует учитываются оба эффекта, оба они будут индуцировать части напряженности электрического поля. Если теперь мы снова рассмотрим интеграл от произведения Edl по замкнутому контуру, то мы можем разделить это соотношение на две части. Первый из них - это то, что происходит с рамкой, контуром, если только магнитное поле изменилось во времени. Другая часть Закона Фарадея - это то, что происходит с контуром, если магнитное поле стабильно, статично, но контур меняет свою конфигурацию. И, наконец, мы получим это соотношение:

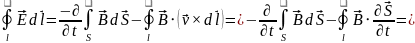
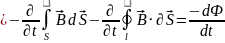
Это соотношение соответствует Закону Фарадея в случае движущегося проводника, и то же соотношение справедливо в случае, когда как конфигурация катушки, так и плотность магнитного потока зависят от времени. В обоих случаях это полное соотношение является правильным и должно использоваться.

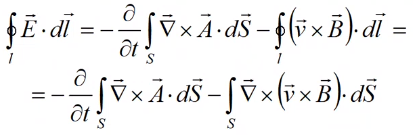Давайте рассмотрим некоторые свойства, общие свойства электромагнитного поля, когда рассматривается этот универсальный (как индукция, так и конфигурация катушки зависят от времени) случай. Использование векторного магнитного потенциала:

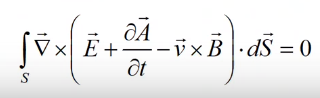(Теорема Гаусса для ротора вектора)

Или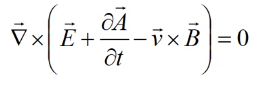

Последнее выражение верно для любой поверхности, поэтому:

Вывод: Завиток этой круглой скобки равен нулю. Почему это так важно? Мы уже говорили о векторах, которые имеют нулевой изгиб. Итак, если завиток функции равен нулю, то мы можем выразить его как градиент некоторой функции. Давайте сделаем это и здесь.

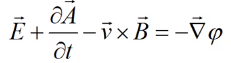Вводя подходящую скалярную функцию φ, мы можем записать: это общее выражение, которое может быть использовано в случае статического поля, динамического поля, полей, изменяющихся во времени, статического поля с движущимся проводником.

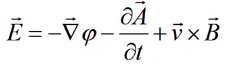
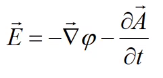Здесь мы можем выразить отдельно вектор E: напряженность поля E здесь - это та, которую наблюдатель "увидел бы" при движении вместе с проводником.

Затем наблюдатель, находящийся в состоянии покоя, видит поле:

18. Unipolar generator (униполярный генератор).

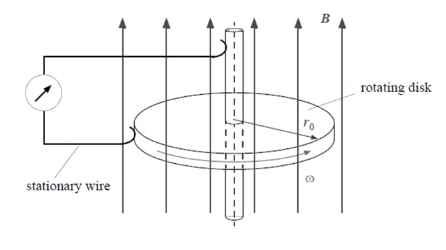Здесь у нас есть вращающееся колесо, проводящее колесо и внешняя магнитная индукция, которая параллельна оси этого колеса. Это колесо вращается с некоторой угловой скоростью и имеет щеточные контакты. Один из этих щеточных контактов прикреплен к оси, другой прикреплен к круглой части колеса. Этот контур вертикальный, он вообще не пересекается магнитным полем.

Результатом этой замкнутой цепи является индуцированная ЭДС.

Как напряжение может быть наведено в этом контуре? У нас нет изменяющегося магнитного потока. Но эксперимент показывает нам, что напряжение существует.

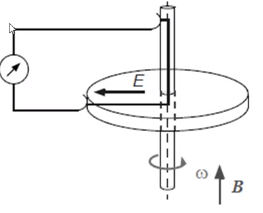
Поток, проходящий через контур, постоянен! Ф=0

Скорость зависит от расстояния до центра:

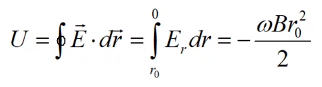Напряженность электрического поля:

Итак, поле действительно будет наведено, но что делать с потоком? Она всегда равна нулю, теория говорит нам, что в универсальном случае индуцированная электродвижущая сила равна полной производной dФ/dt со знаком минус, что неприменимо для данного случая.

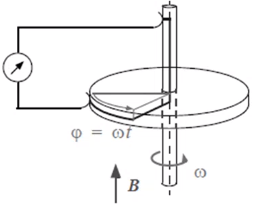Второй случай, что мы должны рассмотреть эту систему еще более подробно. Контур более сложный, чем мы видели в начале. Ток проходит вдоль этой линии, но тогда на самом деле он не может пройти через эту линию, потому что это движущийся объект. И ток действительно идет по радиусу, но радиус движется сам по себе. Наконец, ток будет двигаться вдоль такой кривой линии. Тем не менее, давайте попробуем проанализировать магнитный поток, который пересекает этот треугольник. Площадь этого треугольника равна

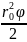
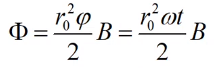
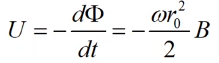Магнитный поток в этом случае:

Наведенная ЭДС:

Однако это объяснение не очень убедительно. Что всегда верно: Использование потока в этой конкретной ситуации не имеет смысла.