
- •Н.Э. Самойленко а.Б. Антиликаторов Основы автоматики и системы автоматического управления:
- •Учебное пособие
- •Утверждено Редакционно-издательским советом университета в качестве учебного пособия
- •Введение
- •Основные понятия
- •1.1. Структура сау
- •1.2. Классификация сау
- •Программы и законы управления
- •1.4. Основные элементы автоматики
- •Статические характеристики элементов сау
- •1.6 Динамические характеристики элементов
- •Линейные динамические звенья сау
- •2.1. Основные характеристиеи лдз
- •2.2. Временные и частотные характеристики
- •2.3 Основные типы лдз
- •2.4. Способы соединения звеньев сау
- •3. Устойчивость линейных систем
- •Понятие устойчивости
- •3.2. Математическая постановка задачи
- •Оценка устойчивости сау по корням
- •3.3. Алгебраический критерий устойчивости
- •3.4. Частотные критерии устойчивости сау
- •4. ЦИфровые системы автоматики
- •4.1. Определение дискретной системы.
- •4.2 Методы математического описания
- •Разностные уравнения вход-выход.
- •2)Описание линейной системы при помощи взвешенной временной последовательности
- •3)Описание линейной системы при помощи разностных уравнений в переменных системах.
- •4.3 Прохождение непрерывного сигнала через
- •4.5 Некоторые свойства z-преобразования
- •Теорема о начальном значении. Предположим, что задано z – преобразование f(z) и требуется определить начальные значения f(0) последовательности.
- •Синтез дискретных систем
- •4.8 Простейшие дискретные линейные системы и цифровые фильтры
- •Нерекурсивный фильтр
- •5. Описание систем радиоавтоматики
- •5.1. Системы частотной автоподстройки
- •5.2. Системы фазовой автоподстройки
- •5.3. Системы слежения за временным положением импульсного сигнала
- •5.4. Угломерные следящие системы
- •5.5. Обобщенные функциональные и структурные схемы радиотехнических следящих систем
- •5.6. Системы автоматической регулировки усиления
- •6. Содержание учебной дисциплины
- •Раздел 1. Введение ( 2 часа)
- •Раздел 2. Основные понятия теории управления и сау ( 2 часа)
- •Раздел 3. Линейные сау ( 12 часов)
- •Раздел 4. Нелинейные сау (6 час.)
- •Раздел 5. Цифровые сау (6 часов)
- •Раздел 6. Оптимальные сау (4 часа)
- •Раздел 7. Перспективы развития сау (2 часа)
- •7. Исследование динамических
- •Лабораторный практикум
- •7.1. Общие указания
- •7.2. Лабораторная работа №1. Исследование линейных динамических звеньев сар
- •Лабораторно-практические задания и методические указания по их выполнению
- •Лабораторные задания и методические указания по их выполнению
- •Работе №1
- •7.3. Лабораторная работа № 2.
- •Лабораторные задания и методические указания по их выполнению
- •Контрольные вопросы по лабораторной работе №2
- •7.4.Лабораторная работа № 3. Исследование устойчивости сар
- •Математическая модель исследуемой системы
- •Лабораторные исследования влияния дополнительных звеньев на устойчивость простейших систем
- •Контрольные вопросы по лабораторной работе №3
- •7.5 Лабораторная работа №4. Исследование сар по их нелинейным моделям
- •Модель системы
- •Лабораторно-практическое задание и методические указания по его выполнению
- •Лабораторное задание и методические указания по его выполнению
- •8. Синтез дискретной сар на основе аналогового прототипа. Курсовая работа
4.5 Некоторые свойства z-преобразования
Z–преобразование обладает рядом свойств, позволяющих анализировать особенности ДЛС. Приведем лишь теоремы о начальном и конечном значениях.
Теорема о начальном значении. Предположим, что задано z – преобразование f(z) и требуется определить начальные значения f(0) последовательности.
По определению
![]() (4.32)
(4.32)
Этот ряд сходится
при всех
![]() ,
поэтому при всех
,
поэтому при всех
![]()
![]()
Теорема о конечном значении. Ограничим последовательность f (кг ), положив К = N, где N– достаточно большое число. Образуем функцию f(kr-r), запаздывающую относительно f (кr ) на r . Если
![]()
![]() ,
(4.33)
,
(4.33)
то Z – преобразование для fn (кг) будет
![]() (4.34)
(4.34)
Найдем разность FN (Z) и FN-1(Z) при Z = 1;
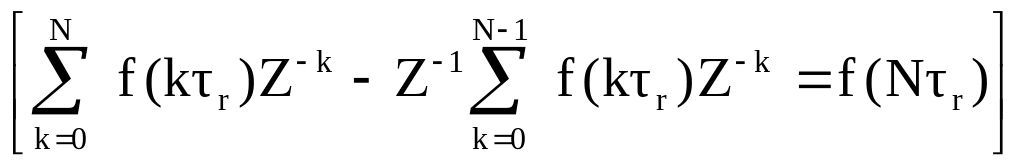
Пусть
![]() ,
тогда
,
тогда
![]() (4.35)
(4.35)
Формула (4.35) устанавливает связь между Z - преобразованием и конечным значением функции.
4.6 Z-передаточная функция дискретной системы
Разностные уравнения вход-выход имеют вид:
![]() (4.36)
(4.36)
Число y(k)характеризует выход в момент кr (шаг дискретизации r обычно опускают). Числа y(k-1), y(k-2) характеризуют предыдущее значение выхода, запоминаемые в памяти ЭВМ.
Аналогично числа и U(k), и U(k-1)характеризуют вход в дискретные моменты k, k-1, … и т.д., они также хранятся в памяти машины.
Уравнение (4.36) называют рекурсивным или разностным, позволяющим вычислить каждое последующее значение выхода по предыдущим данным.
Положим в (4.36)
![]() ,
(4.37)
,
(4.37)
где
![]() -
дельта – последовательность Кронекера
-
дельта – последовательность Кронекера
(![]() -импульс
– одиночный). Подставляя (4.36) в (4.35),
получим реакцию системы,
которую
обозначим через K(k):
-импульс
– одиночный). Подставляя (4.36) в (4.35),
получим реакцию системы,
которую
обозначим через K(k):
![]() (4.38)
(4.38)
Взвешенную временную последовательность (4.38) называют весовой (рис. 4. 11)
Если импульс воздействует на вход не при k = 0, а в произвольный момент (в j – той позиции ), то реакция системы


Рис. 4. 11
в k – той позиции будет (для k ≥ j )
![]() , (4.39)
, (4.39)
где
![]() - коэффициент для входного воздействия.
- коэффициент для входного воздействия.
В общем случае, когда входная последовательность представляет сумму (поток) дельта последовательностей, приложенных в моменты k= 0, 1, 2, …, то есть,
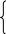
![]()
![]()
временную последовательность на основании принципа суперпозиции на выходе можно определить как
![]() (4.40)
(4.40)
или, после замены переменных m = k – j
![]() (4.41)
(4.41)
Выражение (4.41) – аналог интеграла свертки для непрерывных систем. Воспользуемся (4.9) в самом общем виде:
![]() ,
(4.42)
,
(4.42)
где К(k) – взвешенная временная последовательность, g(m) – дискретизированный входной сигнал.
Взяв Z – преобразование от (4.42), получим
![]() ;
;
или (для правой части (4.11)):
![]() (4.43)
(4.43)
С
(4.44)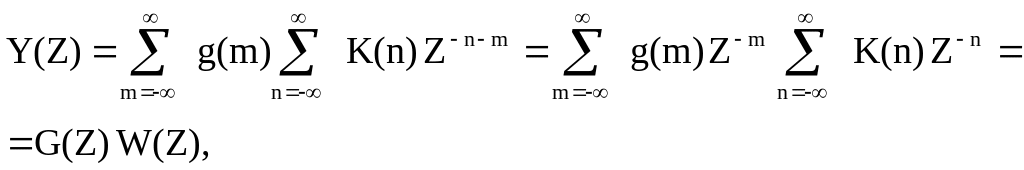
(4.45)![]() .
.
W(Z) называют Z – передаточной функцией дискретной системы. Через Y(Z) и G(Z) обозначены Z–преобразования последовательностей y(nr) и g(nr), то есть, выходной и входной последовательностей.
Пример Z – передаточной функции. Пусть необходимо определить W(Z), соответствующую s – передаточной функции:
![]() (4.46)
(4.46)
Посмотрим вначале – какой непрерывной системе соответствует s - передаточная функция (1.46). Взяв обратное преобразование Лапласа от W(s), получим
![]() (4.47)
(4.47)
где K(t) – импульсная переходная функция, или функция веса, то есть, реакция системы на единичный - импульс (t). Далее от (4.47) перейдем к дискретной весовой временной последовательности согласно правилу:
![]() (4.48)
(4.48)
то есть,
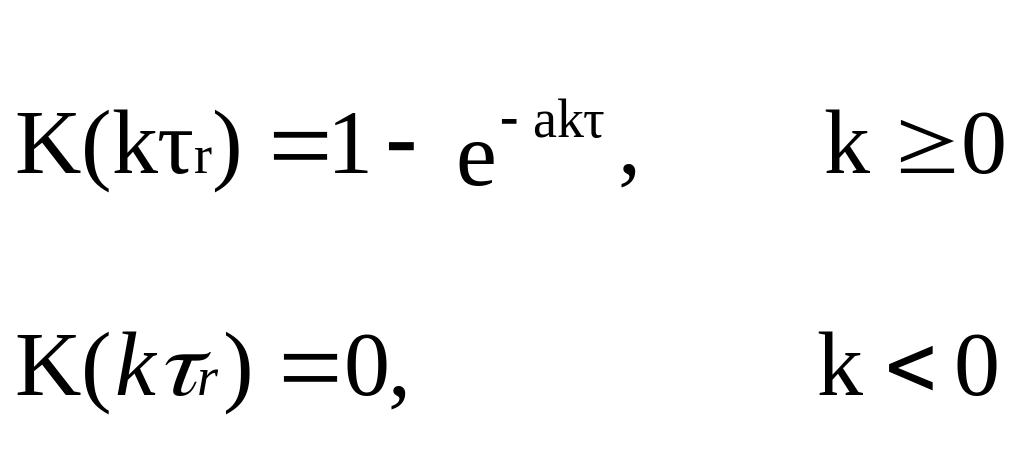 (4.49)
(4.49)
Z – преобразование этой последовательности и будет представлять Z - передаточную функцию, соответствующую s – передаточной функции непрерывной системы (4.46):
![]() ,
(4.50)
,
(4.50)
Описанный здесь способ получения Z – преобразования по s – преобразованию Лапласа позволяет осуществлять синтез дискретных систем по известным характеристикам исходных аналоговых систем.
