Глава 5. Конечно-элементные модели. Метод конечных элементов

5.1. Общий ход решения задачи на основе метода конечных элементов

Решение задач анализа при функциональном моделировании сводится к определению вектора V, который удовлетворяет ис­ходным уравнениям задачи и граничным условиям. Часто ис­комую функцию задают в виде ряда

, (5.1)

где – базисные функции от независимых перемен­ных,

– неизвестные постоянные коэффициенты.

Методы определения постоянных коэффициентов весьма раз­нообразны. Так, в методе Ритца их находят из условия минимума потенциальной энергии системы, в методе коллокаций – из условия удовлетворения дифференциальных уравнений задачи в отдельных точках и т. д. Выбор базисных функций в конечном счете определяет успех решения задачи: если эти функции подо­браны удачно, решение получается простым, в противном случае приходится удерживать большое число членов ряда (9.1), что существенно затрудняет расчет и не всегда приводит к желаемым результатам. Для простых случаев разработаны рекомендации по выбору базисных функций, в сложных случаях проблема на­значения этих функций может оказаться не проще решения неход­кой задачи.

Идея метода конечных элементов (МКЭ) заключается в том, что вместо поиска единого аналитического представления функции v используют ее кусочно-линейную аппроксимацию, т.е. всю область решения разбивают на подобласти конечных размеров, достаточно малых, чтобы обеспечить требуемую точность линеаризации.

Рассмотрим основы МКЭ на примере одномерной задачи, точное решение которой описывается кривой, изображенной на рис. 5.1, а. Прежде всего разбейте область на конечные элементы и т. д. В пределах длины каждого элемента искомую функцию можно считать линейной (рис. 5.1, б):

. (5.2)

Если тем или иным способом вам удастся определить значе­ния искомой функции в узлах , то задача будет решенной, поскольку с учетом равенства (5.2) вы получите возможность вычислить приближенные значения функции в лю­бой точке. Рассмотрим, как можно определить значения искомой функции в узлах .

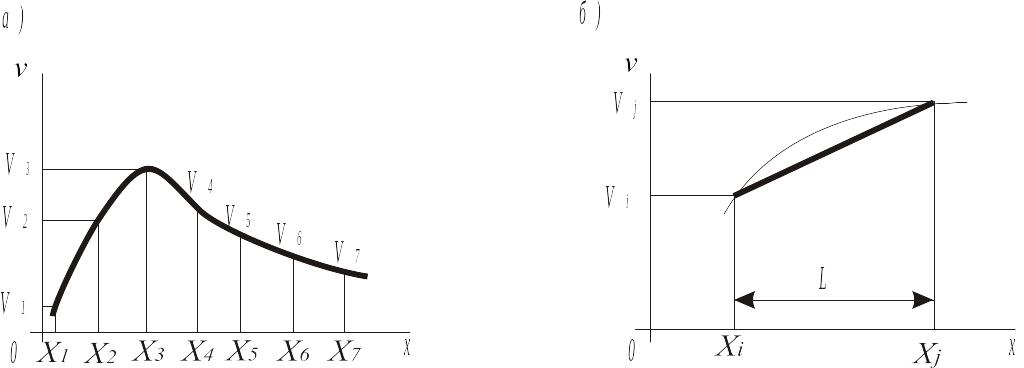
Рис. 5.1. Одномерные конечные элементы

Узловые значения функций вы можете искать различными способами, исходя из физического смысла задачи. Задача может быть задана в форме дифференциальных уравнений, либо в виде некоторого функционала . В первом случае удобно вос­пользоваться методом Бубнова – Галеркина, минимизируя ошибку приближенного решения, во втором – каким-нибудь ва­риационным принципом, обеспечивающим минимизацию функ­ционала. Используя кусочно-линейное представление функции и записывая функционал в виде , вы обеспечите реализацию минимума энергии, приравнивая нулю частные про­изводные:

В результате будет получена система уравнений решение которой позволит вычислить вектор , т.е. найти значения искомой функции в узлах и тем самым решить задачу.

Унификация вычислительных процедур накладывает некото­рые особенности на реализацию МКЭ, для уяснения которых вновь обратимся к решению одномерной задачи (рис. 4.1).

В общем случае алгоритм МКЭ состоит из четырех этапов:

1. выделение конечных элементов (разбиение заданной области на конечные элементы);

2. определение аппроксимирующей функции для отдельного конечного элемента (определение функции элемента);

3. объединение конечных элементов в ансамбль;

4. определение вектора узловых значений функции.

Первый этап будет подробно рассмотрен отдельно. В данном примере суть его понятна без пояснений: выделено шесть конеч­ных элементов в общем случае разных по длине.

Второй этап. Рассмотрим (рис. 5.1, б) один из выделенных элементов (одномерный симплекс-элемент). Для определе­ния коэффициентов а и b полинома (5.2) запишем граничные условия:

при

при

Подставляя эти значения в равенство (5.2), получим систему двух уравнений, решив которую относительно а и b, имеем

.

Подставляя эти коэффициенты в формулу (5.2), можно записать:

(5.3)

Члены уравнения (5.3), заключенные в скобки, называют функци­ями формы одномерного симплекс-элемента:

. (5.4)

С учетом обозначений (5.4) уравнение (5.3) принимает вид:

, (5.5)

или в матричной форме

, (5.6)

где – матрица-строка,

– вектор-столбец.

Полученные здесь формулы (5.4), (5.6) полностью характеризуют одномерный симплекс элемент. Они являются общими пригодными для решения любых задач, включающих одномерные прямолинейные конечные элементы.

Третий этап – объединение конечных элементов в ансамбль. Основу этого этапа составляет замена номеров узлов i и j в уравнении (5.5) на номера, присвоенные узлам в процессе разбиения рассматриваемой области. Для примера, приведенного на рис. 5.1, будем иметь:

Полученная система уравнений представляет собой математи­ческую модель исследуемой задачи. Запишем эту систему в рас­ширенной форме:

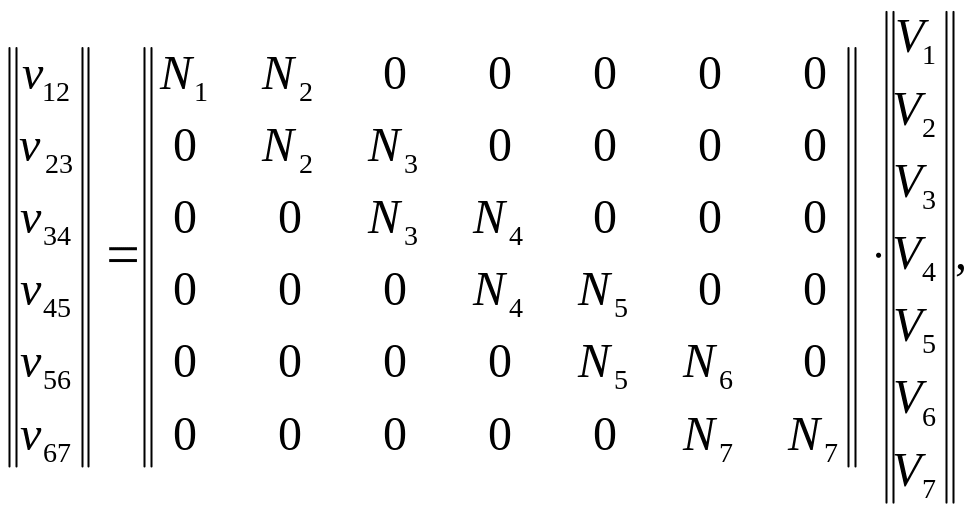(5.7)

что соответствует векторной записи модели

(5.7а)

Четвертый этап – определение вектора узловых значений функции. Этот этап не является формальным, и мы не можем ограничиться ссылкой на рис. 5.1 абстрактного примера. Нужно знать конкретное дифференциальное уравнение или конкретный функционал исследуемого явления.

Допустим, что в нашем примере этот функционал имеет простейший вид:

(5.8)

Разобьем пределы интегрирования в соответствии с делением области на конечные элементы, тогда

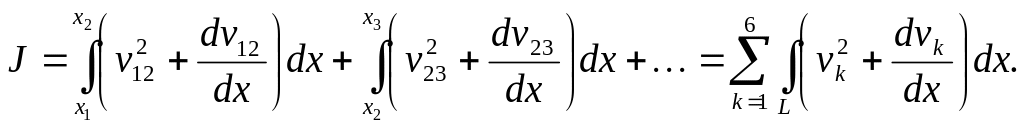
Первый член подынтегрального выражения определим, возведя в квадрат равенство (5.5), второй – путем его дифференцирования с учетом обозначений (5.4). Выполняя интегрирование и простейшие преобразования, можем записать:

(5.9)

где

Для того, чтобы определить минимум функционала (5.9), при­равняем нулю частные производные, предварительно развернув выражения сумм для всех шести конечных элементов и заменяя индексы i, j номерами соответствующих узлов:

. . .

Таким образом, получена следующая система уравнений:

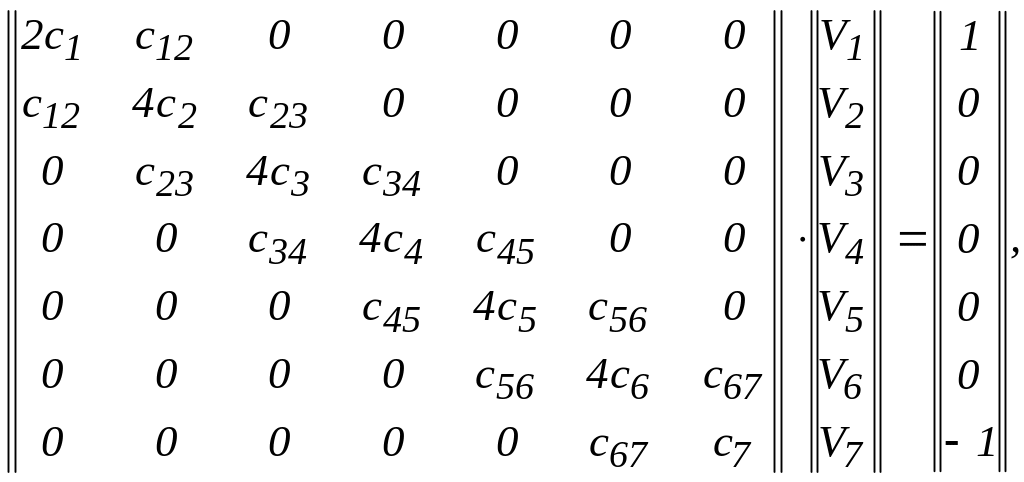
или

. (5.10)

Матрицу С называют матрицей жесткости, а вектор – век­тором нагрузок. Эти названия пришли из строительной меха­ники. Они отвечают сущности рассматриваемых там задач, по­скольку МКЭ первоначально был разработан и в основном сформировался применительно к расчетам строительных конструкций. Затем метод конечных элементов был распространен на другие предметные области, а термины строительной механики сохранились и стали общепринятыми, хотя и отражали иную физическую сущность.

Дальнейший расчет сводится к обращению матрицы С и опре­делению вектора . Зная компоненты вектора и ис­пользуя систему уравнений (5.7), можно вычислить значение ис­комой функции в любой точке. Таким образом, задача полно­стью решена.

Выше было отмечено, что узловые значения функции опреде­ляются дифференциальным уравнением задачи или условием минимизации некоторого функционала. В ряде случаев эти опе­рации не требуется выполнять в явном виде. Можно использо­вать какой-нибудь другой принцип, отвечающий физической сущ­ности задачи. Так, используя уравнения метода перемещений при расчете строительных конструкций, мы автоматически миними­зируем функционал энергии системы, поскольку канонические уравнения указанного метода являются следствием такой мини­мизации.

При рассмотрении примера (рис. 5.1) конечная задача состояла в определении функции . Часто такая функция может быть лишь промежуточным звеном между координатой х и другой переменной, подлежащей определению. Так, уравне­ние изогнутой оси балки интересует нас не как геометрический объект конфигурации системы, а как функция, позволяющая вычислить изгибающие моменты и поперечные силы или нор­мальные и касательные напряжения. В таком случае соответст­вующие зависимости между этими величинами могут быть вклю­чены в состав конечных элементов и в их ансамбль.