3.6. Аналитические модели сложных систем

Математическое моделирование позволяет устанавливать зависимости выходных (y₁, у₂, ..., у_n) переменных от входных переменных (x₁, x₂ ,..., х_n) при целенаправленном изменении внутренних параметров (h₁, h₂,..., h_n) с учетом в ряде случаев воздействия внешней среды. Наиболее просто эта задача решается, если известна функциональная зависимость между соответствующими многомерными векторами:

(3.29)

В таком виде математическую модель удается получить только для очень простых ситуаций. В обычных условиях математическое описание процессов в исследуемом объекте задают в форме системы дифференциальных уравнений. Понятно, что ЭВМ не может непосредственно оперировать даже с простейшими зависимостями типа (3.29), поэтому построение математических моделей подразумевает комплекс преобразований этих зависимостей до уровня, допускающего численное решение, и последующую реализацию такого решения на основе программ анализа в виде элементарных арифметических и логических операций.

В простейших ситуациях исходная задача может быть представлена системой линейных алгебраических уравнений, которая легко сводится к последовательности элементарных операций (ПЭО) на основе стандартных процедур с использованием библиотечных программ. Если модель задана системой нелинейных алгебраических уравнений, то возможны либо непосредственный переход к ПЭО, либо предварительная линеаризация с дальнейшим переходом к ПЭО (рис. 3.10).

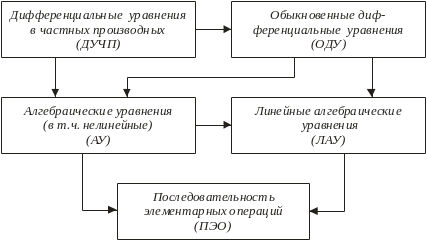
Рис. 3.10. Преобразования уравнений при построении аналитических моделей

Наиболее типичными являются модели, в которых исследуемый процесс описывается обыкновенными дифференциальными уравнениями или дифференциальными уравнениями в частных производных. Численные решения таких уравнений основаны на дискретизации переменных или алгебраизации задачи. Дискретизация заключается в замене непрерывных переменных конечным множеством их значений в заданных для исследования интервалах, а алгебраизация – в замене производных алгебраическими соотношениями, Если дифференциальные уравнения в частных производных описывают статическое состояние, то дискретизация и алгебраизация преобразуют дифференциальные уравнения в систему алгебраических уравнений, в общем случае нелинейных. Так, если рассматриваются переменные, изменяющиеся в пространстве и во времени, то при решении задачи на первом этапе устраняются производные по пространственным координатам, что позволяет перейти к обыкновенным дифференциальным уравнениям, а затем – производные по времени с переходом к алгебраическим уравнениям. Дальнейшее решение задачи может выполняться на основе метода простых итераций, либо быть сведено к предварительной линеаризации на основе метода Ньютона с переходом к линейным алгебраическим уравнениям. Решение системы таких уравнений выполняется с помощью прямых методов, например, метода Гаусса.

Ниже рассмотрена цепочка последовательных преобразований, которая позволяет однотипными приемами решать различные задачи. За базовое принято численное решение дифференциальных уравнений первого порядка с заданными начальными условиями (задача Коши) и системы таких уравнений. К подобным уравнениям может быть приведено обыкновенное дифференциальное уравнение n-го порядка. Дифференциальное уравнение с заданными граничными условиями может быть представлено как редукция к задаче Коши и тем самым решено аналогичными способами.