4.2. Источники энергии и преобразователи. Аналоги топологических уравнений

Условное графическое изображение источников энергии типа Е и I показано на рис. 4.5.

На рис. 4.6, а приведена схема трансформатора, имеющего математическую модель

(4.7)

где Т – коэффициент трансформации.

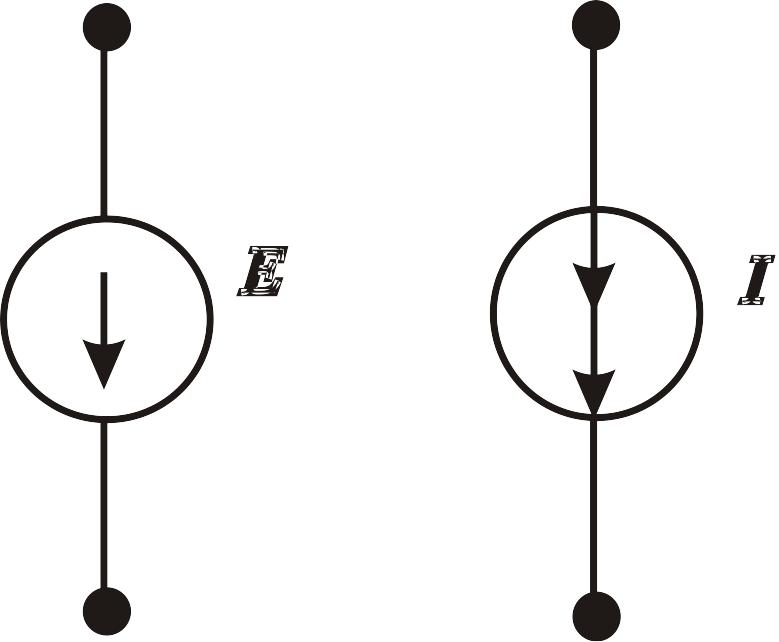
Рис. 4.5. Источники энергии

Примерами трансформаторов в механических подсистемах могут служить рычаги энергии и редукторы.

Гиратор (рис. 4.6, б) имеет модель

(4.8)

где G – коэффициент гирации.

Примером гиратора может служить гидроцилиндр, в котором давление Р преобразуется в силу F, действующую на поршень.

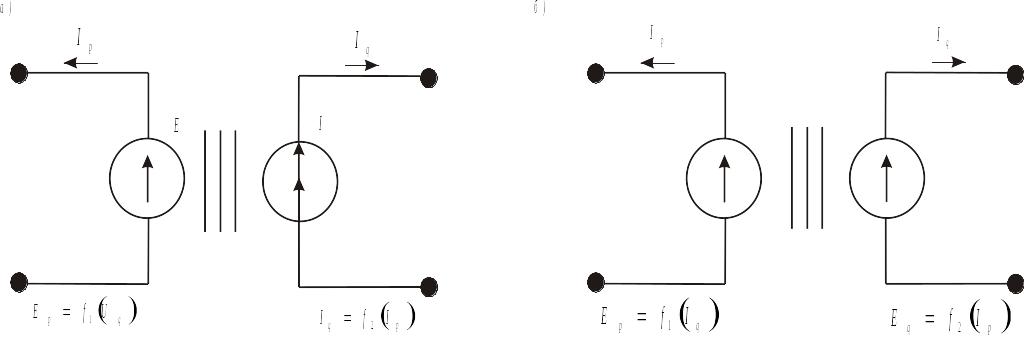
Рис. 4.6. Схемы трансформаторной (а) и гираторной (б) связи

Топологические уравнения типа (4.7), (4.8) в большинстве физических подсистем базируются на уравнениях равновесия и уравнениях неразрывности. Ниже рассмотрены аналогии топо­логических уравнений в подсистемах различной физической при­роды. Условимся снабжать индексом i элементы, примыкающие к данному узлу, а индексом j – входящие в данный контур, при этом в знаках суммы (∑) обозначения « » или « », где p_, q – соответственно множество ветвей, примыкающих к узлу i и входящих в контур j, будем опускать.

Электрическая подсистема

Уравнения равновесия определяют равенство нулю суммы то­ков в узлах сопряжения элементов; их находят по первому закону Кирхгофа:

(4.9)

Уравнения неразрывности соответствуют второму закону Кирхгофа. Они выражают равенство нулю суммы падений напря­жений на элементах схемы, образующих контур:

. (4.10)

Механическая подсистема

Уравнения равновесия отражают принцип Д' Аламбера: сумма сил, действующих на тело, включая инерционные, равна нулю:

(4.9 а)

Для вращательных подсистем суммируются моменты сил, действующих относительно оси вращения.

Уравнения неразрывности определяются принципом сложения скоростей: абсолютная скорость является суммой относительной и переносных скоростей (которых может быть несколько: с перво­го тела на второе, со второго на третье и т. д.).

. (4.10 а)

Для вращательных подсистем следует суммировать угловые скорости.

Гидравлическая (пневматическая) подсистема

Уравнения равновесия определяют равенство нулю потоков Q, подтекающих к узлу или оттекающих от него:

(4.9 б)

Уравнения неразрывности соответствуют сумме падений давлений при обходе по контуру:

. (4.10 б)

Тепловая подсистема

Уравнения равновесия определяют равенство нулю суммы теп­ловых потоков , подтекающих или оттекающих от узла, т. е.

(4.9 в)

Уравнения неразрывности соответствуют сумме разности тем­ператур T_j на участках, входящих в замкнутый контур:

. (4.10 в)

Источники энергии типа потока J и разности потенциалов Е делят на независимые и зависимые.

Независимые источники используют для моделирования по­стоянных воздействий на объект, например, сила тяжести может быть отражена постоянным источником силы F, напряжение питания электрической схемы – источником типа разности по­тенциалов.

Зависимые источники делят на две группы: источники, зависи­мые от времени, и источники, зависимые от фазовых переменных. Первые используют для моделирования внешних воздействий, вторые – для отражения нелинейных свойств объекта, а также для отражения взаимосвязей между подсистемами различной физической природы.

Примером взаимной зависимости двух подсистем p и q раз­личной физической природы может служить трансформаторная связь этих подсистем (см. рис. 4.6). Зависимый источник раз­ности потенциалов в одной подсистеме зависит от разности потенциалов на зависимом источнике потока другой подсистемы, который, в свою очередь, зависит от потока через первый источник.

Эквивалентные схемы технических объектов строят путем объединения в ансамбль всех элементов подсистем (в том числе различной физической природы), образующих данный техничес­кий объект. В эквивалентной схеме отражаются элементы и свой­ства реального объекта, оказывающие существенное влияние на его функционирование.

Двухполюсники (рис. 4.2...4.6), моделирующие элемен­ты и (или) компоненты подсистем, соединяют между собой в со­ответствии со структурой подсистемы и с учетом функциональных связей между компонентами. В первую очередь рекомендуется объединять наиболее существенные элементы. Так, при моделировании механических подсистем вначале выделяют компоненты типа массы. Один из полюсов двухполюсника (рис. 4.2, б) соединяют с базовым узлом, отражающим инерциальную систему отсчета, второй полюс характеризует воздействие этой массы на некоторые элементы объекта, поэтому его следует соединить с полюсами этих элементов. Далее в механической подсистеме выделяют элементы трения и упругости. Элементы трения (рис. 4.4) включают между контактирующими телами, элементы упругости (рис. 4.3) – между телами, соединенными упругой связью. Внешние силы отображают включением источника силы между базисным и тем узлом, к которому подключен элемент массы, подверженной действию этой силы.

Построение эквивалентных схем рассмотрим на конкретных примерах.

Муфта сцепления автомобиля (рис. 4.7) служит для регулирования плавного соединения коленчатого вала двигателя с первичным валом коробки передач.

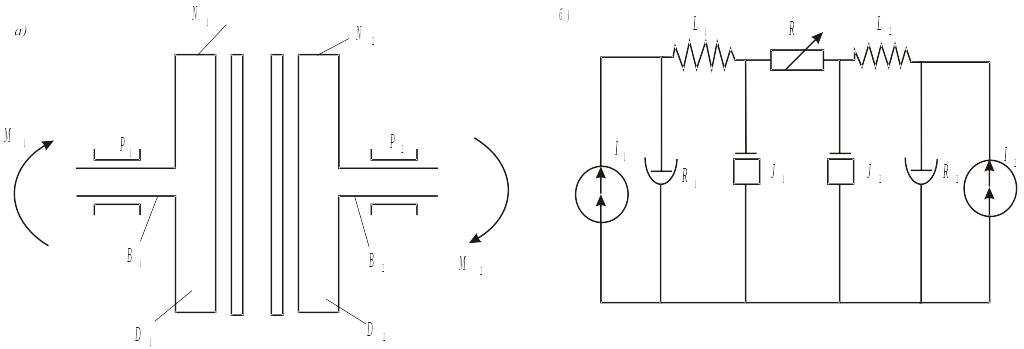
Рис. 4.7. Муфта сцепления (а) и её эквивалентная схема (б)

Крутящий момент через вал имеющий крутильную жесткость передается на маховик и диск с фрикционной накладкой . Суммарный момент инерции ведущего диска равен . Небольшая часть крутящего момента теряется в подшипнике с коэффициентом трения . Когда диски прижаты друг к другу, крутящий момент через фрикционные накладки передается на ведомый диск и далее через вал , на коробку передач.

Эквивалентная схема полностью отражает механизм передачи крутящего момента от двигателя до коробки передач. Момент моделируется током трение в подшипнике – резистором , гибкость вала – индуктивностью , масса ведущего диска – моментом инерции . Работу фрикционных накладок отражает резистор R. Дальнейшая передача момента от диска до коробки передач аналогична рассмотренной.

Примером механической поступательной системы (рис. 4.8) служит автомобиль массой , который перевозит груз массой и прицеп массой . В прицепе находится подпружиненный груз массой .

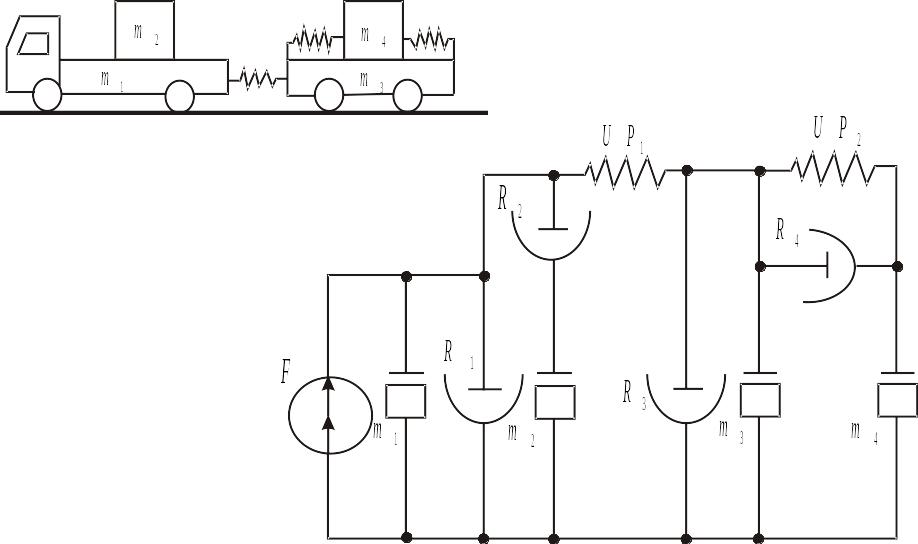
Рис. 4.8. Поступательная механическая система и её

эквивалентная схема

На рисунке F – тяга автомобиля; и – приведенные коэффициенты трения между грузами и кузовами автомобиля и прицепа; и – упругости сцепления и пружины крепления груза к прицепу.

В качестве примера системы, состоящей из электрической, механической и пневматической подсистем, рассмотрим вибро­насос (рис. 4.9). Под воздействием переменного магнитного поля, возникающего в зазоре электромагнита, приходит в движение груз массой т. Этот груз, шарнирно связанный через рычаг с насосом, действует на сильфон S, который, пульсируя, про­качивает воздух через клапаны k.

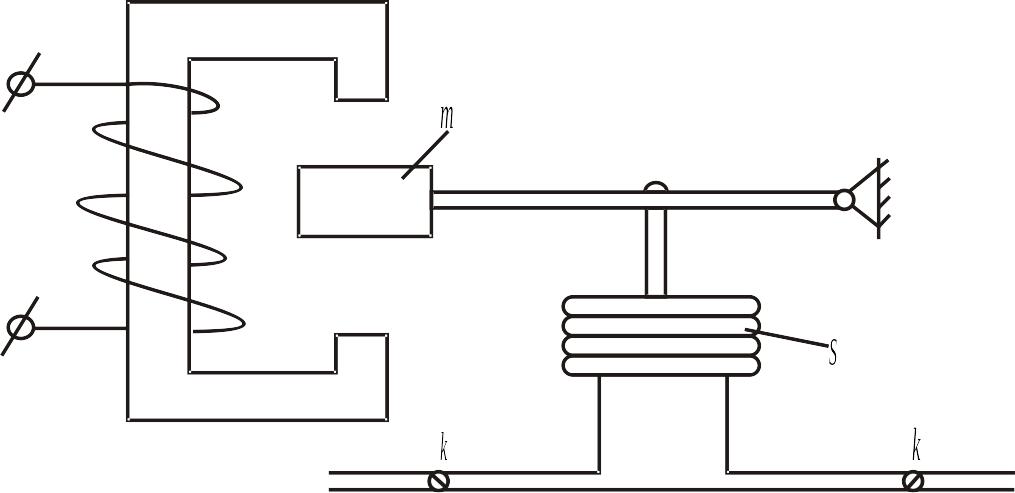
Рис. 4.9. Схема вибронасоса

В устройстве можно выделить конструктивно самостоятельные про­стые подсистемы, доказанные на эквивалентной схеме замещения (рис. 4.10): обмотку электромагнита 1, электромагнит 2, рычаж­ный механизм 3, сильфон и воздушную магистраль с клапаном 4. Связи этих подсистем осуществляются гираторами для пар 1-2 и 3-4 и трансформатором – для пары 2-3.

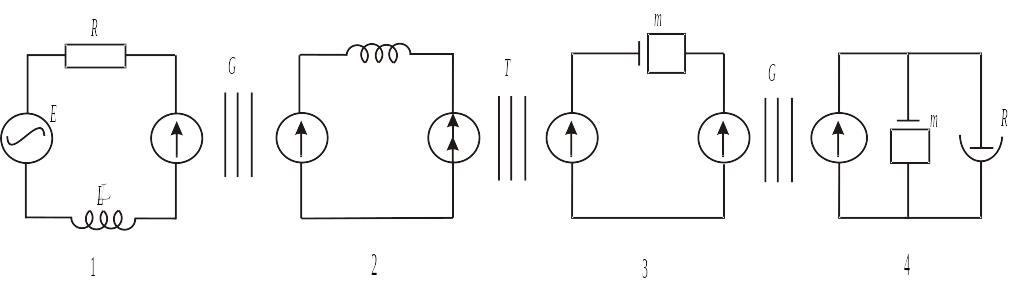
Рис.4.10. Эквивалентная схема замещения вибронасоса