
Методическое пособие 519
.pdfМинистерство образования и науки Российской федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Воронежский государственный архитектурно–строительный университет»
В.Н. Колпачёв, А.М. Дементьева, В.В. Горяйнов
РЕШЕНИЕ ТЕСТОВЫХ ЗАДАНИЙ ФЕДЕРАЛЬНОГО ИНТЕРНЕТ-ЭКЗАМЕНА ПО МАТЕМАТИКЕ
Часть 1. Алгебра и геометрия
Учебное пособие
Рекомендовано в качестве учебного пособия научно-методическим советом Воронежского государственного архитектурно–строительного университета
для студентов всех специальностей и направлений подготовки бакалавров
Воронеж 2012
УДК 51(075):378.244.1 ББК 22.1в6я7 К615
Рецензенты:
кафедра алгебры и топологических методов анализа Воронежского государственного университета;
А.Д. Чернышов, д–р физ.–мат. наук, проф. кафедры высшей математики Воронежской государственной технологической академии
Колпачёв, В.Н.
Решение тестовых заданий федерального интернет-экзамена
К615 по математике: учеб. пособие в 3 ч. – Ч.1: Алгебра и геометрия / В.Н. Колпачёв, А.М. Дементьева, В.В. Горяйнов; Воронежский ГАСУ – Воронеж, 2012. – 151 с.
Предлагаемое учебное пособие содержит подробное решение 160 тестовых заданий федерального интернет-экзамена по математике, составленных из таких дидактических единиц, как «Абстрактная алгебра», «Линейная алгебра», «Аналитическая геометрия» и «Дифференциальная геометрия». Даны теоретические сведения по соответствующим разделам. Кроме этого, в пособии приведен критерий оценки результатов тестирования, описаны все формы тестовых заданий, встречающихся в тестировании, представлена методика репетиционного тестирования для студентов и тематическая структура аттестационных педагогических измерительных материалов.
Пособие предназначено для самостоятельной работы студентов всех специальностей и направлений подготовки бакалавров Воронежского государственного архитектурно– строительного университета при подготовке к федеральному интернет-экзамену по математике, к промежуточной и итоговой аттестации. Также пособие может быть использовано преподавателями для проведения практических занятий со студентами всех форм обучения.
Ил. 59. Табл. 5. Библиогр.: 12 назв.
УДК 51(075):378.244.1 ББК 22.1в6я7
ISBN 978-5-89040-378-0 |
© Колпачёв В.Н., |
|
Дементьева А.М., |
|
Горяйнов В.В., 2012 |
|
© Воронежский ГАСУ, 2012 |
2
ОГЛАВЛЕНИЕ |
|
Введение……………………….………………………………………..... |
5 |
1. Абстрактная алгебра………………………………………………… |
7 |
1.1. Краткие теоретические сведения……………………………….. |
7 |
1.1.1. Элементы теории множеств……………………………… |
7 |
1.1.2. Основные алгебраические структуры…………………… |
9 |
1.1.3.Векторные пространства…………………………………. 11
1.1.4.Линейные отображения…………………………………... 12
1.1.5.Алгебра многочленов……………………………………... 13
1.2. Тестовые задания и их решения………………………………… |
15 |
1.2.1. Основные алгебраические структуры…………………… |
15 |
1.2.2.Бинарные алгебраические операции…………………….. 17
1.2.3.Векторные пространства…………………………………. 19
1.2.4.Линейные отображения…………………………………... 21
1.2.5.Алгебра многочленов……………………………………... 23
2.Линейная алгебра…………………………………………………….. 29
2.1.Краткие теоретические сведения………………………………... 29
2.1.1.Определители. Вычисление определителей…………….. 29
2.1.2.Матрицы…………………………………………………… 31
2.1.3. Системы линейных алгебраических уравнений………… |
34 |
2.1.4. Собственные векторы и собственные значения матрицы |
38 |
2.1.5. Квадратичные формы……………………………………... |
39 |
2.2. Тестовые задания и их решения………………………………… |
40 |
2.2.1.Вычисление определителей………………………………. 40
2.2.2.Матрицы: основные определения………………………... 43
2.2.3.Линейные операции над матрицами……………………... 46
2.2.4.Умножение матриц………………………………………... 48
2.2.5.Обратная матрица…………………………………………. 52
2.2.6.Ранг матрицы……………………………………………… 54
2.2.7.Системы линейных уравнений: основные понятия…….. 57
2.2.8.Системы линейных уравнений: методы решения………. 60
2.2.9. Собственные векторы и собственные значения матрицы 65
2.2.10.Квадратичные формы……………………………………. 67
3.Аналитическая геометрия. Элементы дифференциальной геометрии……………………………………………………………... 69
3.1.Краткие теоретические сведения………………………………... 69
3.1.1.Основные задачи аналитической геометрии на
плоскости………………………………………………….. 69
3.1.2.Полярная система координат…………………………….. 70
3.1.3.Прямая на плоскости……………………………………… 71
3.1.4.Кривые второго порядка………………………………….. 76
3
3.1.5.Прямая и плоскость в пространстве……………………... 81
3.1.6.Поверхности второго порядка……………………………. 90
3.1.7.Кривизна плоской кривой………………………………… 95
3.2.Тестовые задания и их решения ………………………………... 96
3.2.1.Основные задачи аналитической геометрии на
плоскости………………………………………………….. 96
3.2.2.Прямая на плоскости……………………………………… 103
3.2.3.Полярная система координат…………………………….. 115
3.2.4.Кривые второго порядка………………………………….. 120
3.2.5.Основные задачи аналитической геометрии в
пространстве………………………………………………. 124
3.2.6.Прямая и плоскость в пространстве……………………... 126
3.2.7.Поверхности второго порядка
(дифференциальная геометрия поверхностей)…………. 135
3.2.8.Кривизна плоской кривой………………………………… 137
3.2.9.Элементы топологии……………………………………… 138
Заключение………………………………………………………………. 140
Библиографический список…………………..……………………….. 141
Приложение 1. Методика репетиционного тестирования для студентов…………………………………………. 142
Приложение 2. Формы тестовых заданий…………………………… 147
Приложение 3. Тематическая структура аттестационных педагогических измерительных материалов…….. 148
Приложение 4. Критерий оценки результатов тестирования…….. 149
4
ВВЕДЕНИЕ
С 2007 года Воронежский государственный архитектурно-строительный университет участвует в федеральных интернет-экзаменах в сфере высшего профессионального образования (ФЭПО), которые проводит Национальное аккредитационное агентство (Росаккредагентство).
Основной целью проведения интернет-экзамена является оказание помощи вузам при создании систем управления качеством подготовки специалистов на основе независимой внешней оценки. При проведении экзамена используется единый федеральный банк аттестационных педагогических измерительных материалов (АПИМ) и единая технология обработки результатов.
Экзамен проводится в форме компьютерного тестирования и направлен на оценку уровня подготовки студентов на соответствие требованиям государственных образовательных стандартов (ГОС).
Предлагаемое учебное пособие предназначено для самостоятельной работы студентов всех специальностей и направлений подготовки бакалавров Воронежского государственного архитектурно–строительного университета при подготовке к федеральному интернет-экзамену по математике и к промежуточной и итоговой аттестации. Также пособие может быть использовано преподавателями для проведения практических занятий со студентами всех форм обучения.
Пособие содержит подробное решение 160 тестовых заданий федерального интернет-экзамена по математике, составленных из таких дидактических единиц, как «Абстрактная алгебра», «Линейная алгебра», «Аналитическая геометрия» и «Дифференциальная геометрия», а также краткие теоретические сведения по соответствующим разделам, которые предназначены для того, чтобы освежить в памяти студентов ключевые вопросы изученного ранее материала.
Приведенные в пособии примеры тестовых заданий встречались среди АПИМ при тестировании студентов и в демонстрационных материалах (демовариантах) на сайте ФЭПО (http://www.fepo.ru). Количество тестовых заданий, разобранных в учебном пособии, охватывает все темы, которые могут встретиться на тестировании. Но у студентов различных специальностей (направлений подготовки бакалавров) будут присутствовать только те, которые указаны в демоварианте по соответствующей специальности (направлению подготовки бакалавров). Поэтому при подготовке к тестированию в первую очередь студенту нужно обратить внимание именно на эти темы тестовых заданий. Кроме того, следует учесть, что для каждой специальности (каждого направления подготовки бакалавров) демоварианты изменяются два раза в год (весной и осенью). Поэтому пользоваться нужно только обновленными демовариантами.
5
Вучебном пособии тестовые задания приводятся в том виде, который представлен студентам на экране монитора во время тестирования. Слева от вертикальной черты находятся условия заданий, справа – варианты ответа.
Вприложениях к учебному пособию описана методика репетиционного тестирования для студентов, формы тестовых заданий, критерий оценки результатов тестирования и тематическая структура аттестационных педагогических измерительных материалов
Входе работы над пособием авторы пользовались советами, высказанными д.т.н., проф. Т.В. Самодуровой, д.ф.–м.н., проф. А.А. Седаевым и к.ф.–м.н., ст. преп. В.К. Евченко.
6
1.АБСТРАКТНАЯ АЛГЕБРА
1.1.Краткие теоретические сведения
1.1.1. Элементы теории множеств
Операции над множествами
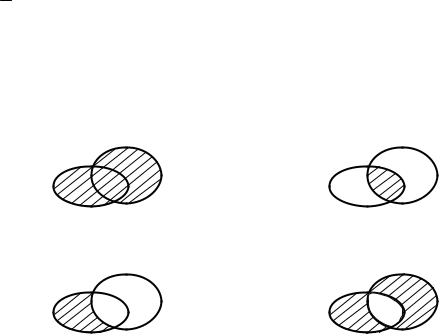
Определение 1.1. Объединением двух множеств A и B называется множество, обозначаемое A B (рис. 1.1), где
A B ={x : x A или x B}.
Определение 1.2. Пересечением двух множеств A и B называется множество, обозначаемое A ∩ B (рис. 1.2), где
A ∩ B ={x : x A и x B}.
Определение 1.3. Разностью двух множеств A и B называется множество, обозначаемое A \ B (рис. 1.3), где
A \ B ={x : x A и x B}.
Определение 1.4. Если A – подмножество множества X (A X ), то множество X \ A называют дополнением множества А до множества Х и обо-
значают A .
Определение 1.5. Симметрической разностью двух множеств A и B на-
зывается множество, обозначаемое A B (рис. 1.4), где
A B =(A\ B) (B \ A).
B |
B |
A |
A |
Рис. 1.1 |
Рис. 1.2 |
B |
B |
A |
A |
Рис. 1.3 |
Рис. 1.4 |
Определение 1.6. Пусть X1 и X 2 |
два непустых множества. Декартовым |
7
произведением этих множеств называется множество, обозначаемое X1 × X2 , |
||
всех упорядоченных пар (x1, x2 ), где x1 X1 , x2 X2 , т.е. |
|
|
X1 × X 2 ={(x1, x2 ): x1 X1 , x2 X 2}. |
|
|
Определение 1.7. Пусть X – непустое множество. Пусть R – некоторое |
||
подмножество произведения X × X |
(R X × X ). Тогда |
R называется бинар- |
ным отношением на множестве X . |
Если пара (x, y) R , |
то пишут x R y и го- |
ворят, что элемент x находится в отношении R с элементом y .
Отображение множеств и классификация отображений
Определение 1.8. Пусть X и Y – два непустых множества. Отображением f множества X в множество Y называется правило, по которому каждо-
му элементу x X ставится в соответствие некоторый элемент y Y .
В этом случае пишут f : X →Y , или X →Y , или y = f (x). Отобра- |
||
|
f |
|
жения называют также функциями, преобразованиями, операторами. |
Если |
|
y = f (x), то элемент y |
называют образом элемента x при отображении f |
. Со- |
ответственно элемент x |
называют прообразом элемента y . Заметим, что образ |
|
y элемента x единственный, а прообразов у элемента y может быть много. |
|
|
Определение 1.9. Отображение f : X →Y называют сюръективным, ес- |
||
ли для любого y Y существует хотя бы один x X , такой что y = f (x). |
|
|
Определение 1.10. Отображение f : X →Y называют инъективным, ес- |
||
ли из равенства f (x1 )= f (x2 ) следует, что x1 = x2 , т.е. разные элементы множе-
ства X отображаются в разные элементы множества Y . Такое отображение на-
зывают также взаимно однозначным.
Определение 1.11. Отображение f : |
X →Y называют биективным, если |
|
оно инъективно и сюръективно. |
|
|
Определение 1.12. Пусть |
f : X →Y |
– биективное отображение. Тогда |
для любого y Y существует |
единственный элемент x X , такой что |
|
y = f (x). Это значит, что каждому y Y поставлен в соответствие некоторый x X , т.е. задано отображение множества Y в множество X . Это отображение называют обратным к отображению f и обозначают f −1 , т.е. x = f −1 (y).
8
Определение 1.13. Множества X и Y называют эквивалентными или изоморфными, если существует биективное отображение f : X →Y .
Определение 1.14. Эквивалентные множества называют множествами, имеющими одинаковую мощность.
Определение 1.15. Множество, эквивалентное множеству N натуральных чисел, называют счетным.
Определение 1.16. Множество, эквивалентное множеству точек отрезка
[0; 1], называют множеством мощности континуума.
1.1.2. Основные алгебраические структуры
Алгебраические операции
Определение 1.17. Пусть S – непустое множество. Говорят, что на S задана алгебраическая операция (бинарная операция или внутренний закон композиции), если задано отображение ϕ : S ×S → S , т.е. каждой паре элементов
(a, b) из S по некоторому правилу ставится в соответствие определенный элемент из S . Этот элемент обозначают ϕ(a, b), или aϕb , или a b . Наиболее
распространены мультипликативная форма записи ϕ(a, b)= ab |
и аддитивная |
форма записи ϕ(a, b)= a +b . В первом случае a и b называют сомножителями |
|
и ab – произведением, а во втором a и b – слагаемыми, а (a +b) |
– суммой. |
Определение 1.18. Пусть множество S1 S и на множестве S задана бинарная операция ϕ(a, b). Говорят, что множество S1 замкнуто относительно
операции ϕ , если для любых a S1 и b S1 ϕ(a, b) S1 . |
|
|
Определение 1.19. Множество вместе с заданными на нем бинарными |
||
операциями называют алгебраической структурой. |
|
|
Группы, кольца, поля, алгебры |
|
|
Определение 1.20. Множество G |
с заданной бинарной |
операцией |
ϕ : G ×G →G (обозначают ϕ(x, y)= x y |
и называют умножением) |
называют |
группой, если справедливы свойства:
9
●x(yz)=(xy)z – ассоциативность;
●существует элемент e G , называемый единицей, такой что xe = ex = x для любого x G ;
●для любого x G существует элемент y G такой, что xy = yx = e ( y –
элемент, обратный к элементу x ).
Определение 1.21. Группа G называется абелевой, если для любых x G и y G выполнено условие xy = yx (перестановочность).
В абелевой группе бинарная операция чаще называется сложением ( x y = x + y ). Соответственно единица группы называется нулевым элементом
(обозначается 0), а обратный элемент к элементу x называется противоположным к x и обозначается “ −x ”.
Определение 1.22. Множество A , на котором заданы две алгебраические операции, называемые соответственно сложением (a +b) и умножением (ab),
называется кольцом, если выполнены условия:
● A – абелева группа относительно сложения; ● справедливы равенства
a(bc)=(ab)c , (a +b)c = ac +bc , c(a +b)= ca +cb
для любых элементов a, b, c A ;
● если A содержит единицу e (ea = ae = a для a A), то e ≠ 0 .
Определение 1.23. Кольцо, содержащее единицу e , в котором все ненулевые элементы имеют обратные и выполнен перестановочный закон относительно умножения (xy = yx), называется полем.
Обычно элементы поля называют числами и единица поля обозначается 1.
Число вида a b−1 обозначается |
a . |
|
|
|
b |
Определение 1.24. Пусть K и X два непустых множества. Отображение |
||
f : K × X → X |
называется внешним законом композиции на множестве X . |
|
Элемент f (α, |
x), α K , x X |
обозначают αx . |
Определение 1.25. Кольцо A называют алгеброй над полем K , если на кольце A задан внешний закон композиции f : K × A → A, при этом для лю-
бых a, b X и любых α, β K выполнены условия:
● (α + β)a =αa + βa ;
10
