Методическое пособие 519
.pdf
Тестовое задание 3.29
Укажите правильное соответствие между характером расположения прямой L : Ax + By +C = 0 на декартовой плос-
кости и значениями коэффициентов А,
В, С.
1.L параллельна оси Ox
2.L параллельна оси Oy
3.L пересекает оси Ox , Oy и не про-
ходит через точку O(0; 0)
υ2 υ2 |
A ≠ 0, B ≠ 0, C = 0 |
υ2 υ2 |
A = 0, B = 0, C = 0 |
υ222 |
A ≠ 0, B = 0, C ≠ 0 |
υ |
|
υ212 |
A = 0, B ≠ 0, C ≠ 0 |
υ |
|
υ232 |
A ≠ 0, B ≠ 0, C ≠ 0 |
υ |
|
Решение. Ранее, получив общее уравнение прямой (3.9), исследовалось расположение прямой в системе координат при равенстве нулю некоторых коэффициентов уравнения. Поэтому делаем вывод, что прямая 1 соответствует четвертому ответу; прямая 2 соответствует третьему ответу; прямая 3 соответствует пятому ответу.
|
Тестовое задание 3.30 |
|
|
||||||
Вектор |
s =(p; −3) параллелен пря- |
|
|
2 |
|||||
|
|
||||||||
|
|
x −5 |
|
y +10 |
|
|
|
||
мой |
|
= |
. Тогда значение p |
|
|
−2 |
|||
|
2 |
|
−3 |
|
|
−4,5 |
|||
|
|
|
|
|
|
|
|||
равно… |
|
|
|
|
|
|
−6 |
||
|
|
|
|
|
|
|
|
|
|
Решение. Данное уравнение имеет вид (3.12), т.е. является каноническим. В этом уравнении вектор {m; n} ={2; −3} является направляющим вектором, т.е.
вектором, параллельным прямой. Если данный вектор s =(p; −3) параллелен прямой, то он коллинеарен вектору {2; −3}, а значит, координаты этих векторов пропорциональны:
2p = −−33 ,
откуда p = 2 , что соответствует первому ответу.
В тестовых заданиях 3.31 – 3.33 используются условия параллельности прямых.
111
|
Тестовое задание 3.31 |
|
|
||
Среди прямых |
|
l1 |
и l3 |
||
|
|||||
l1 |
: x +5y +10 = 0 , |
|
|||
|
l4 |
и l3 |
|||
l2 |
: 2x +10 y −5 = 0 |
, |
|||
l2 |
и l3 |
||||
l3 |
: 2x −10 y −10 = 0 , |
||||
l1 |
и l2 |
||||
l4 : −2x +10 y −10 = 0 |
|||||
|
|
||||
параллельными являются … |
|
|
|||
Решение. В этом задании даны общие уравнения (3.9) прямых. Условие параллельности прямых – пропорциональность коэффициентов при одинаковых переменных в их общих уравнениях. У прямых l1 и l2
|
|
|
1 |
= |
5 |
|
, |
|
|
|
||
|
|
|
2 |
10 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||
значит, l1 |
l2 |
– соответствует четвертому ответу. |
||||||||||
У прямых l3 и l4 |
2 |
|
|
−10 |
|
|
|
|||||
|
|
|
|
= |
, |
|
|
|||||
значит, l3 |
l4 |
|
|
−2 |
10 |
|
|
|||||
|
|
|
|
|
|
|||||||
– соответствует второму ответу. |
|
|
||||||||||
Первый и третий ответ неверны, так как |
||||||||||||
|
|
1 ≠ |
5 |
|
и |
2 |
≠ |
10 |
. |
|||
|
|
−10 |
2 |
|
||||||||
|
|
2 |
|
|
|
−10 |
||||||
Тестовое задание 3.32
Прямая на плоскости задана уравнением y = 2x +3. Параллельной ей яв- 
ляется прямая с уравнением…
4x −2 y +7 = 0 y −2x +9 = 0 4x + 2 y −5 = 0 y + 2x −3 = 0
Решение. Приведем уравнение данной прямой к общему: 2x − y +3 = 0 .
Воспользуемся условием (3.15′). Сравним данное уравнение с уравнением первого ответа:
24 = −−21 ,
значит, первый ответ верный.
112
Для прямой во втором ответе
−22 = −11 .
Следовательно, второй ответ верный. Для третьего и четвертого ответа
24 ≠ −21 и 22 ≠ −11 ,
поэтому эти ответы неверны.
Тестовое задание 3.33 |
|
|
|
|
|
Прямая, проходящая через две точки |
|
− |
x |
+ y =1 |
|
|
|||||
M0 (1; 3), M1 (4; 2), параллельна пря- |
|
|
|||
3 |
|||||
мым… |
|
|
x |
− y =1 |
|
|
|
3 |
|||
|
|
|
|
||
|
|
|
x |
+ y =1 |
|
|
|
3 |
|||
|
|
x |
|
||
|
|
− |
− y =1 |
||
|
3 |
||||
|
|
|
|
|
|
Решение. Воспользуемся условием параллельности прямых – равенством угловых коэффициентов. У прямой, проходящей через точки M0 и M1 ,
k = 24 −−13 = −13 .
Сравним угловые коэффициенты прямых, предлагаемых в ответах, с чис-
лом −13 , приводя их уравнения к виду (3.6). В первом ответе y = 3x +1, k = 13 ≠ −13 , значит, ответ неверен. Во втором ответе y = 3x −1, k = 13 ≠ −13 , т.е.
ответ неверный. В третьем ответе y = − 3x +1, k = −13 – третий ответ верный. В
четвертом ответе y = − 3x −1, k = −13 – четвертый ответ верен.
113
Тестовое задание 3.34 |
|
|
Уравнение прямой, перпендикулярной |
|
x +5y −13 = 0 |
|
||
прямой y = 6x −5 , является… |
|
|
|
5x − y +1 = 0 |
|
|
|
|
|
|
6x − y −2 = 0 |
|
|
x +6 y −7 = 0 |
|
|
|
Решение. В предлагаемых ответах даны общие уравнения прямых, а данное уравнение представлено в виде (3.6). Поэтому приведем уравнения в ответах к виду (3.6) и воспользуемся условием перпендикулярности прямых (3.16). Угловой коэффициент данной прямой равен k0 = 6 . Следовательно, у прямой,
перпендикулярной данной, должен быть угловой коэффициент k = − |
1 |
= − |
1 . |
||||
k0 |
|||||||
Сравним угловые коэффициенты прямых из ответов с k = −1 . |
|
6 |
|||||
|
|
|
|||||
|
x |
|
6 |
|
|
|
|
В первом ответе y = − |
+13 , т.е. k |
= −1 . Ответ неверен. Во втором ответе |
|||||
|
|||||||
5 |
5 |
5 |
|
|
|
||
y = 5x +1, т.е. k = 5 . Ответ неверен. В третьем ответе y = 6x − 2 , т.е. k = 6 . Ответ неверен. В четвертом ответе y = − 6x + 76 , т.е. k = −16 , т.е. четвертая прямая пер-
пендикулярна данной.
Тестовое задание 3.35 |
|
|
|||
Вектор |
|
|
=(p; 5) перпендикулярен |
|
|
N |
|
10 |
|||
прямой |
2x − y −1 = 0 . Тогда значение |
|
|||
|
−10 |
||||
p равно… |
|
−2,5 |
|||
|
|
|
|
|
2,5 |
|
|
|
|
|
|
Решение. Данное уравнение вида (3.9), поэтому вектор {2; −1} является
нормальным вектором прямой, т.е. перпендикулярен прямой. Так как данный вектор N =(p; 5) тоже перпендикулярен прямой, то векторы {p;5} и {2; −1}
коллинеарны, а значит, их координаты пропорциональны:
2p = −51 .
Следовательно, p = −10 , что соответствует второму ответу.
114
|
|
|
Тестовое задание 3.36 |
|
|
|
|
|
|
|
||||||||||
|
Даны вершины треугольника |
P( |
2; 1), |
|
x + y + 2 = 0 |
|||||||||||||||
|
|
|||||||||||||||||||
|
Q(−1; −1), |
R(3; 2). Тогда |
уравнение |
|
||||||||||||||||
|
|
4x +3y −11 = 0 |
||||||||||||||||||
|
высоты PH имеет вид… |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
2x +3y −13 = 0 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x + 2 y −13 = 0 |
|
|
|
Решение. |
Высота |
PH |
|
|
перпендикулярна стороне QR , значит, вектор |
||||||||||||
|
|
|
|
|
( |
|
( |
|
) |
( |
|
)) |
|
( |
|
|
) |
|
|
|
N |
= QR = |
|
3 − |
|
−1 ; 2 − |
|
−1 |
= |
|
4;3 |
|
является нормальным вектором высоты, по- |
||||||||
этому коэффициенты при неизвестных в общем уравнении высоты пропорцио-
нальны координатам вектора |
|
|
= (4;3) |
(все нормальные векторы данной пря- |
|||||||||||
N |
|||||||||||||||
мой коллинеарны). Для прямых в первом, третьем и четвертом ответах |
|||||||||||||||
|
1 |
≠ |
1 |
, |
2 |
≠ |
|
3 |
, |
3 |
≠ |
2 |
, |
||
4 |
|
4 |
|
4 |
3 |
||||||||||
3 |
|
3 |
|
|
|||||||||||
поэтому эти ответы не подходят. Во втором ответе 44 = 33 . Остается проверить,
лежит ли точка P на предполагаемой прямой. Подставим координаты точки P(2; 1) во второе уравнение:
4 2 +3 1 −11 = 0 ,
т.е. второй ответ верен.
|
|
|
|
|
3.2.3. Полярная система координат |
||||
|
|
Тестовое задание 3.37 |
|
|
|
|
|||
Точка М с декартовыми координатами |
|
r = |
2, ϕ = |
π |
|||||
|
|||||||||
|
3 |
|
1 |
|
|
|
|||
|
|
, |
|
|
имеет полярные координа- |
|
|
|
4 |
2 |
2 |
|
|
|
|||||
|
|
|
|
|
r = |
2, ϕ = |
π |
||
ты… |
|
|
|
|
6 |
||||
|
|
|
|
|
|
||||
r = 2, ϕ = π4 
r =1, ϕ = π6
Решение. Чтобы найти полярные координаты точки М, воспользуемся формулами (3.4), связывающими полярные и декартовы координаты точки:
115
r = |
x |
2 |
+ y |
2 |
|
|
3 |
2 |
|
1 2 |
|
|
x |
|
3 |
|
|
y |
|
1 |
|
||
|
|
= |
|
|
|
+ |
|
|
=1 |
, |
cosϕ = |
|
= |
|
, |
sinϕ = |
|
= |
|
, |
|||
|
|
2 |
2 |
r |
2 |
r |
2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
откуда ϕ = π6 , что соответствует четвертому ответу.
Тестовое задание 3.38
Уравнение окружности, изображенной |
|
r =3cosϕ |
на рисунке, |
|
|
|
r =9 |
|
|
|
|
|
|
r =9sinϕ |
|
|
r =3 |
|
|
|
в полярной системе координат имеет вид…
Решение. На рисунке изображена окружность с центром в начале координат и с радиусом R = 3. Ее уравнение в системе xOy (см. формулу (3.19))
имеет вид x2 + y2 = 9 . Воспользуемся формулами (3.4), выражающими декартовы координаты точки (x; y) через полярные (r;ϕ) и подставим x и y в урав-
нение окружности:
(r cosϕ)2 +(r sinϕ)2 = 9 r2 (cos2 ϕ +sin2 ϕ)= 9 r2 = 9 r = 3.
Уравнение r = 3 – это уравнение данной окружности в полярной системе координат – соответствует четвертому ответу.
Тестовое задание 3.39 |
|
|
|
Уравнение r cosϕ =3 в декартовых |
|
x =3 |
|
|
|
||
координатах имеет вид… |
|
|
|
|
x + y |
=3 |
|
|
|
||
|
|
x2 + y2 =3 |
|
|
|
y =3 |
|
Решение. Так как по формулам (3.4) r cosϕ = x , то данное уравнение |
|||
r cosϕ =3 в декартовой системе координат имеет вид x =3 – соответствует первому ответу.
116
Тестовое задание 3.40
Уравнение x2 + y2 −4by = 0 в поляр- |
|
r = 4bcosϕ |
ных координатах имеет вид… |
|
|
|
r = 4bsinϕ |
|
|
|
|
|
|
r =bsin 2ϕ |
|
|
r =b2 sinϕ |
Решение. Так же, как и в тестовом задании 3.38, подставим x и y (формулы (3.4)) в данное уравнение. Получим
(r cosϕ)2 +(r sinϕ)2 − 4br sinϕ = 0 r2 (cos2 ϕ +sin2 ϕ)− 4br sinϕ = 0r2 − 4br sinϕ = 0 r (r − 4bsinϕ)= 0,
т.е. r = 0 или r = 4bsinϕ. Уравнение r = 4bsinϕ обобщает оба равенства ( r = 0 при ϕ = 0 ), поэтому правильный ответ второй.
Тестовое задание 3.41
На плоскости введена полярная систе- |
|
окружность радиуса 5 с центром в |
ма координат(r ; ϕ). Уравнение ϕ = 25 |
|
|
|
полюсе |
|
|
||
|
||
задает на этой плоскости… |
|
прямую линию |
|
|
окружность радиуса 25 с центром в |
|
|
полюсе |
|
|
|
|
|
|
|
|
луч |
|
|
|
Решение. Данному уравнению соответствуют точки плоскости, у которых полярный угол одинаковый (ϕ = C = const ). Такие точки лежат на луче, выходящем из полюса, составляющем с полярной осью угол C . Поэтому правильный ответ четвертый.
Тестовое задание 3.42
На плоскости введена полярная система координат(r ; ϕ). Уравнение
r2 =81 задает на этой плоскости…
окружность радиуса 9 с центром в полюсе
прямую линию
окружность радиуса 81 с центром в полюсе 
луч
Решение. Из заданного уравнения линии видно, что у всех точек линии полярный радиус r = 9 , т.е. эти точки расположены на расстоянии девять еди-
117
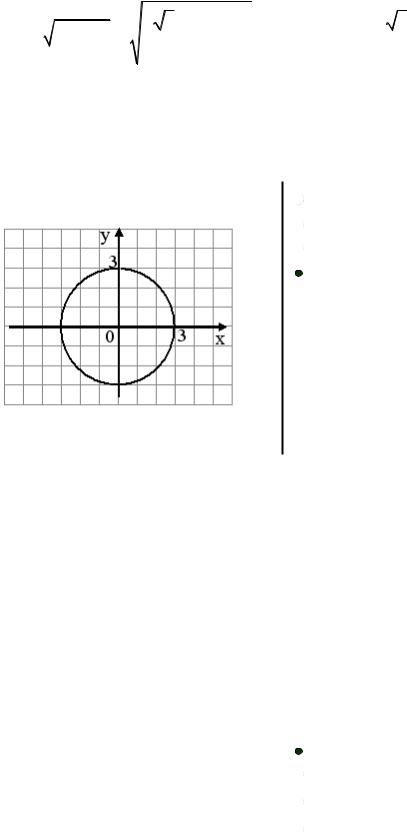
ниц от полюса, а значит, составляют окружность радиуса R = 9 с центром в полюсе. Таким образом, правильный ответ первый.
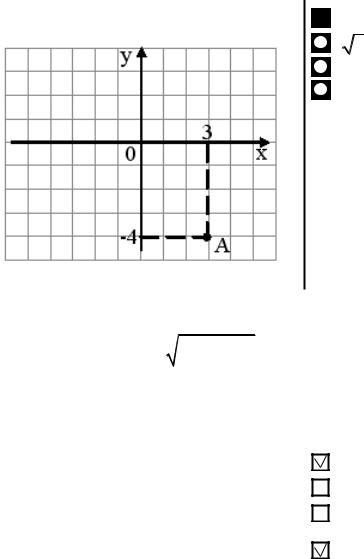
Тестовое задание 3.43
Полярный радиус точки А, изобра- 
5
женной на рисунке,
7
25 7
равен…
Решение. Видно, что декартовы координаты точки A – x = 3 и y = −4.
По формулам (3.4) r = 32 +(−4)2 = 5 . Следовательно, правильный ответ первый.
Тестовое задание 3.44
На плоскости введены прямоугольная |
|
rM = yM |
|
|
|
|||||
и полярная системы координат, |
при- |
|
|
|
|
|||||
ϕM = yM |
|
|
|
|||||||
чем положительная полуось абсцисс |
|
|
|
|||||||
|
rM = − yM |
|
|
|||||||
совпадает |
с |
полярной |
осью. Пусть |
|
|
|
||||
(xM ; yM ) |
– |
декартовы, |
а (rM ; ϕM ) – |
|
ϕM =xM |
+ |
π |
+ 2πk при некотором |
||
полярные координаты точки М, лежа- |
|
2 |
||||||||
|
|
|
|
|
||||||
щей на положительной части оси ор- |
|
целом значении k |
||||||||
динат. Правильными утверждениями |
|
|
|
|
|
|
||||
являются… |
|
|
|
|
|
|
|
|
|
|
Решение. По условию точка M лежит на положительной полуоси орди- |
||||||||||
нат. Очевидно, ее абсцисса xM = 0 , |
а ордината |
yM > 0 , и все точки данной по- |
||||||||
луоси имеют полярный угол ϕ =π |
или ϕ = |
π |
+ 2πk |
(при k = 0; ±1; ± 2;…) и |
||||||
|
|
|
2 |
|
|
2 |
|
|
|
|
полярные радиусы, равные ординатам этих точек. Поэтому правильные ответы
– первый и четвертый (ϕM =π2 + 2πk = 0 + π2 + 2πk = xM + π2 + 2πk , т.к. xM = 0 ).
118
Тестовое задание 3.45
Симметричными относительно полюса О в полярной системе координат на плоскости являются точки…
P1 (1; 0), P2 (1; π )
P1 2; − 35π , P2 2; − 25π
P1 4; − π2 , P2 4; π2
P1 3; 23π , P2 3; π3
Решение. У симметричных относительно полюса точек одинаковые полярные радиусы, а полярные углы отличаются на π (с точностью до целого числа оборотов). Поэтому верные ответы первый и третий: в первом ответе
r = r |
=1, |
ϕ = 0 , ϕ |
2 |
=π , т.е. |
ϕ |
2 |
−ϕ =π ; в третьем ответе r |
= r |
|
= 4 , |
|
ϕ = −π |
, |
|||||||||||||||||||||||||||
1 |
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
2 |
|
|
1 |
2 |
||||||||||
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ϕ2 |
= |
|
, т.е. ϕ2 −ϕ1 |
|
= |
|
|
− |
=π . Второй ответ не подходит, |
так как в нем |
||||||||||||||||||||||||||||||
2 |
|
2 |
− |
2 |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ϕ = − |
3π |
, ϕ |
|
= − |
2π |
|
|
|
и ϕ |
|
−ϕ |
= − |
2π |
− |
|
− |
3π |
|
= π |
≠π + 2πk (k Z ). Четвертый |
||||||||||||||||||||
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||||||||||||||
1 |
|
|
|
5 |
|
|
5 |
|
|
|
|
|
|
|
|
1 |
|
|
5 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
= π |
|
|
|||||||||
ответ |
|
тоже |
|
не |
|
|
|
подходит, |
|
|
так |
|
как |
|
в |
нем |
ϕ = |
|
, |
ϕ |
|
|
и |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
|
|
|
3 |
|
|
|
|
|
|
|
= π |
|
|
2π |
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ϕ2 −ϕ1 |
− |
= − |
|
≠π + 2πk |
|
(k Z ). |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тестовое задание 3.46
Полюс полярной системы координат 
совмещен с началом декартовой сис- 
темы координат, а полярная ось совпадает с положительной полуосью абсцисс. Тогда точка (3; y), заданная в
декартовой системе координат, имеет полярный радиус ρ =5 при у, равном…
±2
2
±4
8
Решение. У данной точки |
(3; y) по формуле (3.4) полярный |
радиус |
r = 32 + y2 . Если по условию r |
= 5, то получим уравнение 9 + y2 |
= 5 , т.е. |
y2 =16 или y = ±4 – верный третий ответ.
119
3.2.4. Кривые второго порядка
Тестовое задание 3.47
Расстояние между фокусами эллипса 12
x2 + y2 =1 равно …
100 64
Решение. У данного эллипса a2 =100 , b2 = 64 (см. формулу (3.20)), по-
этому c = a2 −b2 = |
100 −64 = 6 – это половина фокусного расстояния, т.е. |
|
расстояние между фокусами равно 2c =12 . |
|
|
Ответ: 12. |
|
|
Тестовое задание 3.48 |
|
|
Среди уравнений |
кривых укажите |
(x + 2)2 −(y −1)2 =16 |
уравнения гиперболы. |
|
|
x + y2 =9
x2 − y2 =1 25 16
3x2 + y2 = 25
Решение. Рассмотрим каноническое уравнение гиперболы (3.22) – оно соответствует третьему ответу, а уравнение гиперболы с центром в точке (x0 ; y0 ) и осями симметрии, параллельными координатным осям, соответствует
первому уравнению, так как его можно переписать в виде (x 16+ 2)2 − (y16−1)2 =1,
разделив обе его части на 16.
Тестовое задание 3.49 |
|
|
Если уравнение окружности имеет вид |
|
C (−3; −5), R = 6 |
|
||
(x −3)2 +(y −5)2 =36 , то его центром |
|
C (3; 5), R = 6 |
C и радиусом r являются … |
|
|
|
C (3; 5), R = 36 |
|
|
|
|
|
|
C (−3; −5), R = 36 |
|
|
|
Решение. Сравнив данное уравнение окружности с формулой (3.18), видим, что x0 = 3, y0 = 5, R2 = 36 , т.е. центр окружности C (3; 5), а радиус R = 6 ,
что соответствует второму ответу.
120