Методическое пособие 519

●α(a +b)=αa +αb ;

●α(ab)=(αa)b = a(αb);

●(αβ)a =α(βa);

●1 a = a .

Замечание 1.1. Часто в алгебраической структуре с бинарной операцией ab(a +b) единицу (ноль) называют нейтральным элементом, а обратный (про-

тивоположный) элемент к элементу a называют симметричным элементу a .

1.1.3. Векторные пространства

Определение 1.26. Абелева группа S с бинарной операцией сложения называется линейным (векторным) пространством над полем K , если задан внешний закон композиции f : K ×S → S ( f (α, x) =αx , α K , x S , αx S )

ивыполнены условия:

●1 x = x ;

●(α + β)x =αx + βx ;

●α(x + y)=αx +αy ;

●(αβ)x =α(βx)

для любых x, y S и любых α, β K .

Иными словами, в линейном пространстве элементы можно складывать и можно умножать на числа. При этом в пространстве есть нулевой элемент и действия обладают всеми свойствами сложения и умножения на коэффициент. Элементы линейного пространства называют векторами.

Чаще всего рассматривают линейное пространство над полем K , где K – это поле вещественных или комплексных чисел.

Определение 1.27. Пусть E линейное пространство над полем K . Пусть x1,…, xn – векторы из E , а α1,…,αn – числа из K . Тогда выражение

α1x1 +…+αn xn = y

называют линейной комбинацией элементов x1,…, xn с коэффициентами α1,…,αn . Говорят, что y линейно выражается через векторы x1,…, xn .

Определение 1.28. Векторы x1,…, xn линейного пространства E называ-

ют линейно независимыми, если их линейная комбинация равна нулю лишь с нулевыми коэффициентами. Если же существует линейная комбинация векто-

11

ров y1,…, ym , равная нулю, среди коэффициентов которой есть хотя бы один ненулевой, то векторы y1,…, ym называют линейно зависимыми.

Определение 1.29. Если в векторном пространства E над полем K существует n линейно независимых векторов e1,…,en и любой вектор x E линейно

выражается через эти векторы ( x =α1e1 +…+αnen ), то говорят, что пространство E имеет размерность, равную n ( n – мерно).

Определение 1.30. Любой упорядоченный набор n линейно независимых векторов в n – мерном векторном пространстве называется базисом этого пространства. Коэффициенты разложения любого вектора пространства по векторам базиса определяются однозначно и называются координатами этого вектора в данном базисе.

Множество всех свободных векторов образует трехмерное векторное пространство над полем вещественных чисел. Условие линейной независимости трех векторов – их некомпланарность (непараллельность одной плоскости). Любые четыре вектора линейно зависимы (поэтому–то пространство трехмерно). Если в этом пространстве задан базис, то каждый вектор можно задать тройкой чисел – его координат в этом базисе. Действия с векторами можно осуществлять действиями с их координатами. В частности, если a =(a1; a2 ; a3 )

и b =(b1; b2 ; b3 ), то для любых α и β R

αa + βb =(αa1 + βb1; αa2 + βb2 ; αa3 + βb3 ).

Замечание 1.2. Допускаются обозначения a {a1; a2 ; a3} и b {b1; b2 ; b3}.

1.1.4. Линейные отображения

Определение 1.31. Пусть E линейное пространство над полем K . Отображение f : E → E называется линейным, если выполнено условие

f (αx + β y)=α f (x)+ β f (y)

для любых векторов x, y E и любых чисел α, β K .

Определение 1.32. Пусть E – n - мерное линейное пространство над полем K . Пусть в E задан некоторый базис e1,…,en . Тогда любому линейному

отображению f : E → E соответствует матрица A =(aij ), i, j =1, n , столбцы ко-

12

торой состоят из координат образов Aej базисных векторов ej соответственно.

Иными словами,

Ae1 = a11e1 +…+ an1en ,

.....................................

Aen = a1ne1 +…+ annen .

Матрицу A называют матрицей линейного отображения f в данном базисе.

Если в некотором базисе даны вектор x =(x1,…, xn ) и матрица A линейного отображения f , то координаты образа вектора x можно найти, умножив матрицу A на матрицу – столбец координат вектора x . Иными словами, если y =(y1,…, yn )= f (x), то

1.1.5. Алгебра многочленов

Определение 1.33. Пусть x C (C – множество комплексных чисел). Тогда выражение (функция)

P(x)= a0 + a1x +…+ an xn ,

где a0 ,a1 ,…,an C , называется многочленом степени n ( an ≠ 0 ), а числа a0 ,…,an называются коэффициентами многочлена.

Относительно бинарных операций сложения функций и умножения функций множество всех многочленов степени n ≥ 0 является алгеброй над полем комплексных чисел, т.е. множество многочленов P(x) называют алгеброй

многочленов (обозначается P(C) ).

Определение 1.34. Число x0 называется корнем многочлена P(x), если

P(x0 )= 0.

Теорема 1.1 (основная теорема высшей алгебры). Каждый многочлен P(x) P(C ) степени n ≥1 имеет в C хотя бы один корень.

13

Теорема 1.2. Число x0 C является корнем многочлена P(x) тогда и только тогда, когда P(x) делится на многочлен P1 (x)= x − x0 .

Теорема 1.3. Если P(x)= a0 + a1x +…+ an xn – многочлен степени n ≥1, то справедливо представление

где числа x1,…, xn – корни многочлена.

Многочлен P(x) степени n имеет ровно n корней x1,…, xn C (некоторые из корней могут совпадать друг с другом). Представление P(x) в виде (1.1)

называется разложением многочлена на линейные множители.

Определение 1.35. Число k j называется кратностью корня xj многочлена P(x), если справедливо представление (1.2).

Теорема 1.4. Если два многочлена степени не выше n совпадают в (n +1) различных точках, то эти многочлены тождественно равны.

Теорема 1.5. Для того, чтобы два многочлена P(x) и P* (x) тождествен-

но совпадали, необходимо и достаточно, чтобы у этих многочленов совпадали коэффициенты при одинаковых степенях x .

Теорема 1.6. Если P(x) – многочлен с действительными коэффициентами, то вместе с корнем x1 = a +bi (b ≠ 0) многочлен P(x) имеет корень x2 = a −bi (a,b R).

Теорема 1.7. Если P(x) – многочлен с действительными коэффициентами степени n ≥1, то справедливо представление

P(x)= an (x − x1 )k1 … (x − xs )ks (x2 + p1x + q1 )l1 … (x2 + pr x + qr )lr , (1.3)

14

где x1,…, xs – действительные корни многочлена P(x), а квадратные трехчлены (x2 + pj x + qj ) имеют действительные коэффициенты и соответствуют комплексным попарно сопряженным корням многочлена P(x). При этом k1 +…+ ks + 2l1 +…+ 2lr = n .

Определение 1.36. Многочлен P(x)= a0 + a1x +…+ an xn , где x R и ко-

эффициенты a0 ,a1 ,…,an R , называется многочленом над полем действитель-

ных чисел. Множество всех таких многочленов тоже образует алгебру над полем действительных чисел.

Такие многочлены раскладываются на множители по формуле (1.3).

1.2.Тестовые задания и их решения

1.2.1.Основные алгебраические структуры

Тестовое задание 1.1

В этих заданиях нужно проверить замкнутость данного множества по отношению к каждой из указанных операций. Это означает, что нужно проверить, принадлежит ли результат данной операции исходному множеству.

15

Решение задания 1.1. В этом задании дано множество Z целых чисел. Очевидно, произведение целых чисел и разность целых чисел – целые числа, а корень из целого числа и частное от деления целых чисел не всегда являются целыми числами. Поэтому правильные ответы: операции умножения и вычитания.

Решение задания 1.2. Здесь рассмотрим, какие из операций с натуральными числами всегда дают в результате натуральное число. Очевидно, это

сложение и умножение.

Решение задания 1.3. В этом задании дано множество натуральных чисел, делящихся на 3. Произведение и сумма таких чисел тоже делится на 3, а частное и разность вообще могут и не являться натуральными числами. Значит, правильные ответы: операции сложения и умножения.

Тестовое задание 1.4

В заданиях 1.4 и 1.5 фактически задается вопрос о замкнутости множества относительно двух операций, а вместо этого ставится вопрос о выполнимости операций всегда на данном множестве, т.е. о принадлежности результатов указанных операций с любыми элементами множества тому же множеству.

Решение задания 1.4. В данном задании правильный ответ – умножение

исложение, так как данное множество состоит из положительных четных чисел. Результаты вычитания и деления таких чисел могут быть неположительны

идаже не являться целыми.

Решение задания 1.5. В этом задании рассмотрены те же действия, что и в задании 1.4, но на множестве натуральных чисел с добавленным к ним числом 0. Очевидно, ответ такой же, как и в задании 1.4, и по той же причине.

16

1.2.2. Бинарные алгебраические операции

Решение заданий 1.6. и 1.7. В этих заданиях рассматривается множество N натуральных чисел. Перечислены несколько бинарных операций. Нужно определить, какие из них определены на N, т.е. результат каких из этих операций с любыми натуральными числами есть натуральное число. Очевидно, это опе-

или дроби. Поэтому в заданиях 1.6 и 1.7 правильные ответы – вторая и третья операции.

Тестовое задание 1.8

17

В заданиях 1.8 и 1.9 нужно определить элемент, симметричный (противоположный, обратный ) данному элементу.

Решение задания 1.8. В данном задании дана группа R действительных чисел с операцией умножения, в которой нейтральным элементом является число 1. В этом случае симметричным любому ненулевому числу является об-

ратное ему (числу a ≠ 0 симметричное a−1 = 1a ). Числу 8 симметричным явля-

ется 18 = 0,125.

Решение задания 1.9. Здесь дана группа Z целых чисел с операцией сложения, в которой нейтральным элементом является число 0. В этом случае симметричным любому целому числу является противоположное число (числу a симметрично « −a »). Числу 4 симметричным числом является « −4 ».

Тестовое задание 1.10

Решение. В этом задании рассматривается бинарная операция сложения чисел. Спрашивается, на каких из рассматриваемых числовых множествах она выполнима, т.е. фактически какие из предлагаемых множеств замкнуты относительно операции сложения. Очевидно, эти множества – множество действи-

Решение. В данном задании рассматривается бинарное отношение R делимости на множестве натуральных чисел N. В отношении R находятся такие

18

пары натуральных чисел (a, b), для которых ba – целое число. Спрашивается,

для каких из приведенных четырех множеств пар натуральных чисел все пары этих множеств находятся в отношении R. Для ответа на этот вопрос нужно для каждого множества проверить каждую пару – делится ли первый элемент пары на второй? Очевидно, правильный ответ – второе и четвертое множества. Действительно, во втором множестве 36 делится на 2, 36 делится на 3, 36 делится на 4 и 36 делится на 9. Аналогично проверяется четвертое множество. В первом множестве третий элемент (16;32), а в третьем множестве третий эле-

мент (18;36) нас не устраивают, так как 16 не делится нацело на 32, а 18 на 36.

1.2.3. Векторные пространства

Тестовое задание 1.12

Тройка векторов, образующих базис в пространстве, изображена на рисунках

…

19

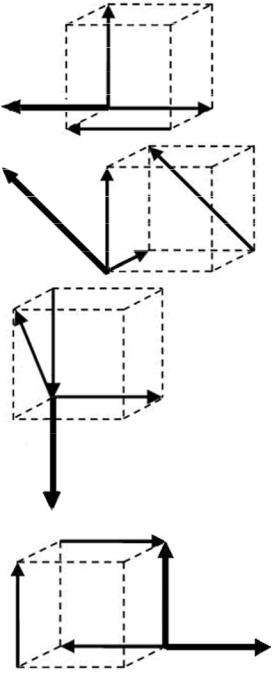
Решение. В этом задании изображены четыре тройки векторов в трехмерном векторном пространстве. Предлагается указать те из этих троек, которые образуют базис в этом пространстве. Так как базис в трехмерном векторном пространстве образует любая тройка линейно независимых векторов, а условие линейной независимости трех векторов – их некомпланарность, то визуально (т.е. глядя на рисунки) определяем, что некомпланарные тройки векторов

– во втором и третьем вариантах предлагаемых ответов. Действительно, выпустив эти векторы из одной точки, получим (перенесенные векторы обозначим толстой линией):

в первом варианте –

во втором варианте –

в третьем варианте –

в четвертом варианте –

Теперь видно, что в первом и четвертом вариантах тройки векторов лежат

20