
Методическое пособие 519
.pdf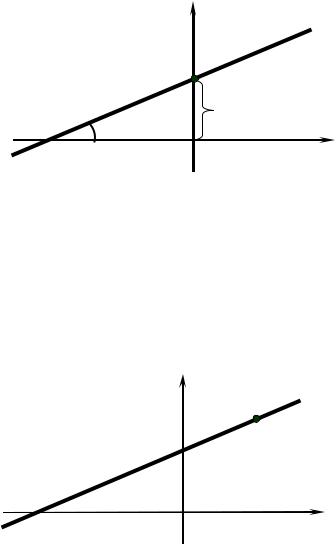
3.1.3. Прямая на плоскости
Уравнение прямой линии на плоскости можно записать по-разному, в зависимости от имеющейся информации об этой прямой.
Определение 3.1. Если прямая неперпендикулярна оси Ox и составляет угол α с положительным направлением оси Ox , измеренный от оси Ox против часовой стрелки, то k = tgα называют угловым коэффициентом прямой.
1. Если известен угловой коэффициент k прямой и отрезок, отсекаемый прямой на оси Oy , равный b (рис. 3.4), то уравнение прямой имеет вид
y = kx +b |
(3.6) |
и называется уравнением прямой с угловым коэффициентом.
y
N (0 ; b ) |
L |
|
|
b |
|
α |
|
0 |
x |
Рис. 3.4 |
|
2. Если известен угловой коэффициент k |
прямой и известна точка |
M0 (x0; y0 ), лежащая на прямой (рис. 3.5), то уравнение прямой имеет вид |
|
y − y0 = k (x − x0 ) |
(3.7) |
и называется уравнением прямой, проходящей через данную точку в данном направлении.
y |
L |
|
M 0 (x0 ; y0 )
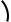 α
α
0 |
x |
Рис. 3.5
71
Определение 3.2. Любой вектор, перпендикулярный прямой, называется
нормальным вектором прямой.
3. Если известен нормальный вектор N {A; B} прямой и прямая проходит через заданную точку M0 (x0; y0 ) (рис. 3.6), то ее уравнение имеет вид
A(x − x0 )+ B(y − y0 )= 0 |
(3.8) |
и называется уравнением прямой, проходящей через данную точку перпендикулярно данному вектору.
y
L |
N {A; B} |
M0 (x0; y0) |
 M (x; y)
M (x; y)
0 |
x |
Рис. 3.6
4. Уравнение любой прямой, имеющей нормальный вектор N {A; B}, за-
писывается в виде |
|
Ax + By +C = 0 |
(3.9) |
и называется общим уравнением прямой.
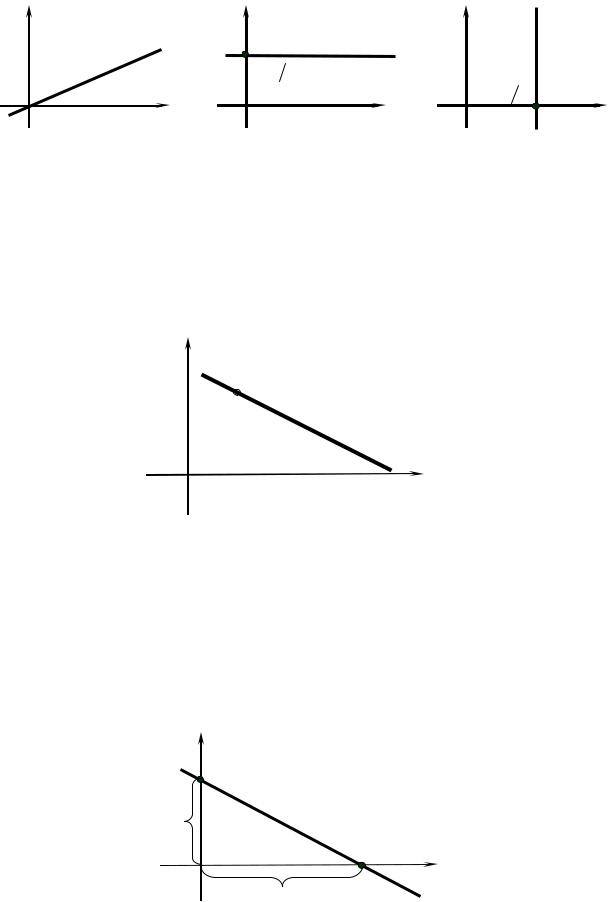
А. Если C = 0 , то Ax + By = 0
начало координат (рис. 3.7).
Б. Если A = 0 , то By +C = 0
раллельна оси Ox (рис. 3.8).
В. Если B = 0 , то Ax +C = 0
раллельна оси Oy (рис. 3.9).
Г. Если A =C = 0 , то By = 0 Д. Если B =C = 0 , то Ax = 0
y = − BA x – прямая L проходит через
y = −C |
|
y = const |
– прямая L па- |
B |
|
|
|
x = −C |
|
x = const |
– прямая L па- |
A |
|
|
|
y = 0 – ось Ox .
x = 0 – ось Oy .
72
y |
y |
L |
L |
|
−C D |
0 |
x |
Рис. 3.7 |
Рис. 3.8 |
5. Если прямая L проходит через точки
y
L
|
−C A |
0 |
x |
Рис. 3.9
M1 (x1; y1 ) и M2 (x2; y2 )
(рис. 3.10), то уравнение прямой, проходящей через две заданные точки, будет имеет вид
x − x1 |
= |
y − y1 |
. |
(3.10) |
|||
|
|
||||||
x |
− x |
|
y |
2 |
− y |
|
|
2 |
1 |
|
|
1 |
|
|
|
y
L
 M1 (x1; y1)
M1 (x1; y1)
 M2 (x2; y2)
M2 (x2; y2)
0 |
x |
Рис. 3.10
6.Если прямая не проходит через начало координат и пересекает ось Oy
вточке M1 (0;b), а ось Ox – в точке M2 (a;0) (рис. 3.11), то ее уравнение имеет вид
x |
+ |
y |
=1, |
(3.11) |
|
a |
b |
||||
|
|
|
и называется уравнением прямой в отрезках.
y
L |
M1 (0; b) |
|
|
b |
M2 (а; 0) |
|
|
0 |
x |
|
а |
Рис. 3.11
73
Определение 3.3. Любой вектор, параллельный прямой, называется на-
правляющим вектором прямой.
7. Если прямая проходит через заданную точку M0 (x0; y0 ) и ее направ-
ляющий вектор S {m; n} (рис. 3.12), то ее уравнение можно записать в виде
x − x0 |
= |
y − y0 |
. |
(3.12) |
m |
|
|||
|
n |
|
||
Оно называется каноническим уравнением прямой.
y
L |
|
{m; n} |
S |
M0 (x0; y0)
M (x; y)
0 |
x |
Рис. 3.12
Прямую, рассмотренную на рис. 3.12, можно задать также параметриче-
ски:
x = x0 |
+tm, |
(3.13) |
|
y = y0 +tn, |
|||
|
|||
где t - это параметр ( −∞ <t < ∞). Уравнения (3.13) называются параметриче-
скими уравнениями прямой.
Угол между двумя прямыми.
Условия параллельности и перпендикулярности двух прямых
|
|
|
Если известны угловые коэффициенты прямых L1 и L2 , равные k1 = tgα1 |
|||||
и |
k |
2 |
= tgα |
2 |
(рис. 3.13), то угол ϕ ≠ |
π между прямыми L |
и L (угол, на кото- |
|
|
|
|
|
2 |
1 |
2 |
||
|
|
|
|
|
|
|
|
|
рый нужно повернуть против часовой стрелки вокруг точки пересечения прямую L1 до совмещения с прямой L2 ) определяется по формуле
tgϕ = |
|
|
k2 −k1 |
|
. |
(3.14) |
||
1 |
|
|
||||||
|
+ k |
2 |
k |
|
|
|||
|
|
|
|
|
1 |
|
|
|
74
y |
L2 |
L1 |
|
|
ϕ |
|
α1 |
α2 |
0 |
|
х |
|
|
|
Рис. 3.13 |
|
|
|
Если прямые L1 и L2 параллельны или совпадают, то |
|
|||||
|
|
|
k2 = k1 . |
|
|
(3.15) |
Если же прямые L1 и L2 перпендикулярны, то |
|
|||||
k |
2 |
k |
= −1 или k = − |
1 |
. |
(3.16) |
|
||||||
|
1 |
1 |
k2 |
|
||
|
|
|
|
|
||
Для прямых, заданных общими уравнениями, проще найти косинусы углов между ними. Если L1 : A1x + B1 y +C1 = 0 , а L2 : A2 x + B2 y +C2 = 0 , то
cosϕ = ± |
|
A1 A2 |
+ B1B2 |
|
. |
(3.14′) |
A2 |
+ B2 |
A2 |
+ B2 |
|||
|
1 |
1 |
2 |
2 |
|
|
Условие параллельности (или совпадения) прямых имеет вид пропорции:
|
A1 |
= |
B1 |
, |
(3.15′) |
|
A |
B |
|||
|
|
|
|
||
2 |
|
2 |
|
|
|
а равенство |
|
|
|
|
|
A1 A2 + B1B2 = 0 |
(3.16′) |
||||
является условием перпендикулярности прямых.
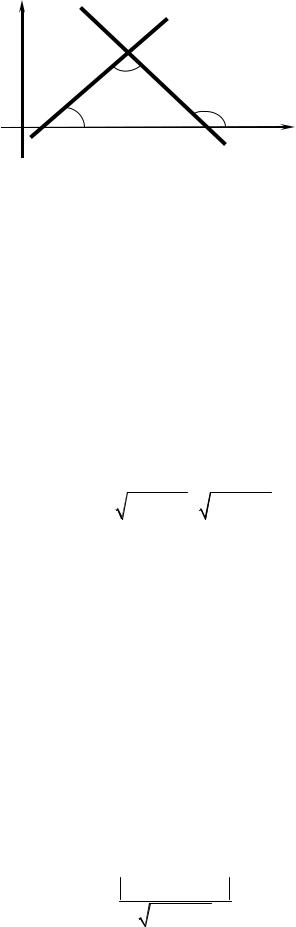
Расстояние от точки до прямой
Если заданы точка M0 (x0; y0 ) и прямая L Ax + By +C = 0 (рис. 3.14), то расстояние d от точки ется по формуле
d = Ax0 + By0 +C .
A2 + B2
своим общим уравнением M0 до прямой L определя-
(3.17)
75
y
L |
M 0 |
|
n {A; B} |
||
|
||
|
d |
|
0 |
х |
Рис. 3.14
3.1.4. Кривые второго порядка
Кривыми второго порядка являются: окружность, эллипс, гипербола и парабола.
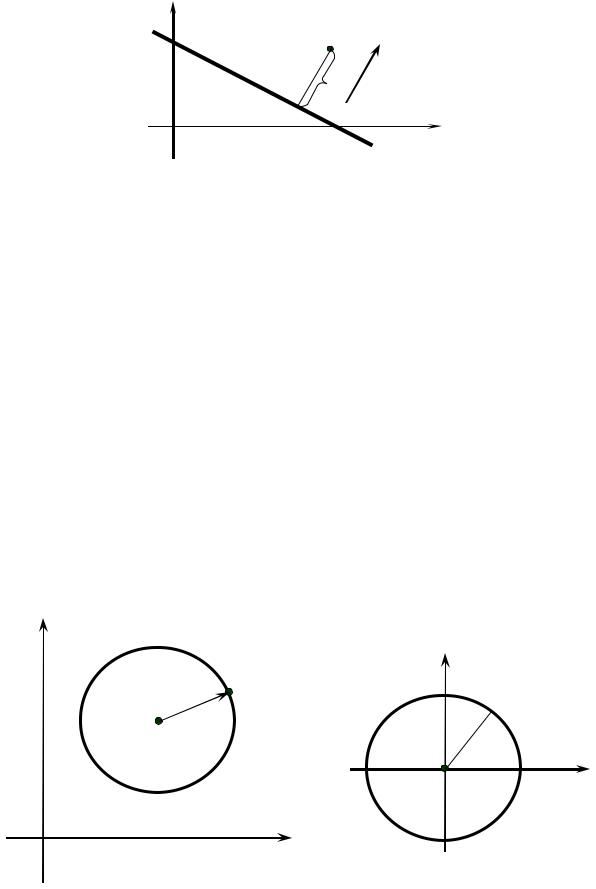
Определение 3.4. Окружностью называется геометрическое место точек на плоскости, равноудаленных от фиксированной точки, называемой центром окружности.
Уравнение окружности радиуса R с центром в точке M0 (x0; y0 )
(рис. 3.15) имеет вид. |
|
|
(x − x |
)2 +(y − y )2 = R2 . |
(3.18) |
0 |
0 |
|
Частным случаем уравнения (3.18) является уравнение |
|
|
|
x2 + y2 = R2 , |
(3.19) |
описывающее окружность с центром в начале координат (рис. 3.16).
у
у
M
M0 R
R
х
0 |
х |
Рис. 3.16
Рис. 3.15
76
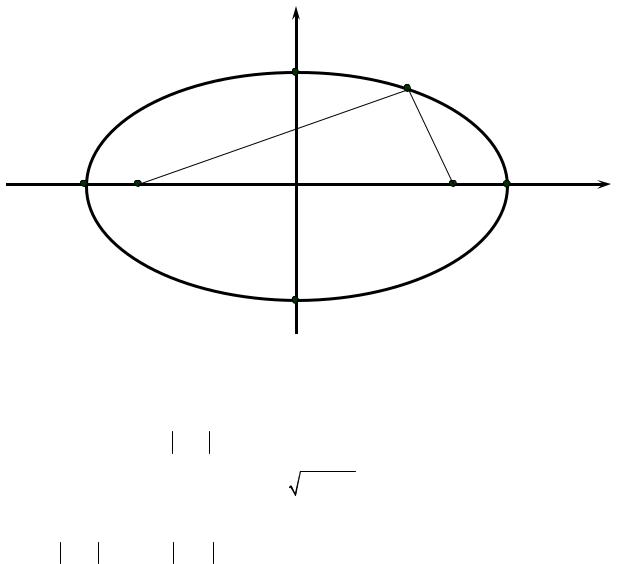
Определение 3.5. Эллипсом называется геометрическое место точек на плоскости, сумма расстояний от каждой из которых до двух данных точек F1 и
F2 , называемых фокусами, есть величина постоянная и большая, чем расстояние между фокусами.
В системе координат, у которой начало расположено в середине отрезка F1F2 и ось Ox проходит через фокусы (рис. 3.17), уравнение эллипса имеет вид
|
|
|
|
|
x2 |
+ |
y2 |
=1 |
|
|
(3.20) |
|
|
|
|
|
a2 |
b2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
и называется каноническим уравнением эллипса. |
|
|
|
||||||||
|
|
|
|
у |
|
|
|
|
|
|
|
|
|
|
|
|
B2 (0;b) |
|
|
|
|||
|
|
|
|
|
|
|
|
M (x; y) |
|
|
|
|
|
|
|
r1 |
|
|
r2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
(−a;0) |
F |
(−c;0) |
0 |
|
|
|
F |
(c;0) |
A |
(a;0) х |
1 |
|
1 |
|
|
|
|
|
2 |
|
2 |
|
B1 (0;−b)
Рис. 3.17
В уравнении (3.20) 2а и 2b называются большой и малой осями эллипса.
Фокусное расстояние F1F2 обозначают 2с. Справедливо соотношение
c = a2 −b2 .
Если M (x; y) – произвольная точка эллипса (см. рис. 3.17), то длины отрезков F1M = r1 и F2M = r2 называются фокальными радиусами точки
M (x; y).
77

Форма эллипса характеризуется отношением |
|
||
|
c |
=ε , |
(3.21) |
|
a |
||
|
|
|
|
называемым эксцентриситетом эллипса, причем 0 <ε <1.
Если эллипс симметричен относительно координатных осей, но его фокусы лежат на оси ординат, то его уравнение имеет вид
y2 + x2 =1. a2 b2
Если оси симметрии эллипса параллельны координатным осям Ox и Oy , то его уравнение имеет вид
(x − x0 )2 |
+ |
(y − y0 )2 |
=1 или |
(y − y0 )2 |
+ |
(x − x0 )2 |
=1, |
|
a2 |
b2 |
|||||||
a2 |
|
b2 |
|
|
|
где x0 и y0 – координаты центра эллипса.
Определение 3.6. Гиперболой называется геометрическое место точек на плоскости, модуль разности расстояний от каждой из которых до двух данных точек F1 и F2 , называемых фокусами, есть величина постоянная и меньшая,
чем расстояние между фокусами.
В системе координат, у которой начало расположено в середине отрезка F1F2 и ось OX проходит через фокусы (рис. 3.18), уравнение гиперболы имеет
вид
x2 |
− |
y2 |
=1, |
(3.22) |
|
a2 |
b2 |
||||
|
|
|
и называется каноническим уравнением гиперболы.
Гипербола (3.22) имеет две асимптоты, определяемые уравнениями
y = b x и |
y = −b x . |
(3.23) |
a |
a |
|
Параметры а и b – действительная и мнимая полуоси гиперболы соответ-
ственно, с – половина фокусного расстояния F1F2 . Справедлива формула
c = a2 +b2 .
78
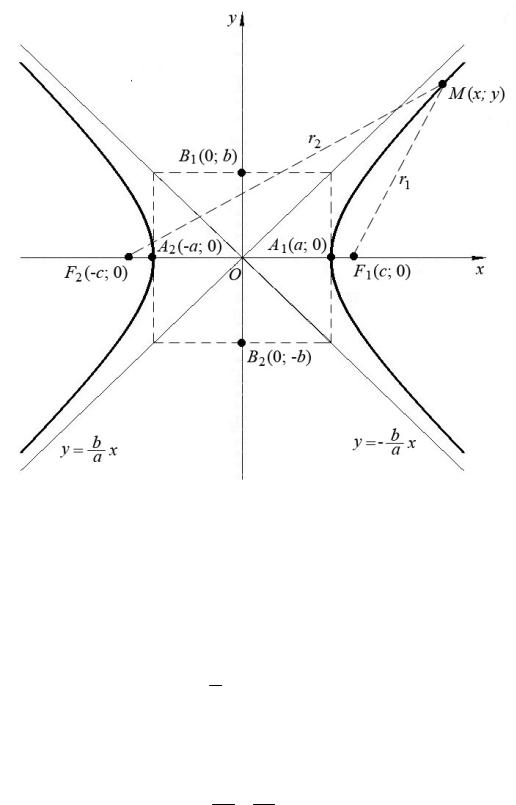
Рис. 3.18
Так же, как у эллипса, расстояния от любой точки M (x; y) гиперболы до фокусов обозначаются r1 и r2 и называются фокальными радиусами точки M (x; y). Форма гиперболы тоже характеризуется эксцентриситетом ε , где
ac =ε , ε >1.
Если начало координат – центр гиперболы и фокусы лежат на оси ординат, то уравнение гиперболы имеет вид
y2 − x2 =1. a2 b2
Если оси симметрии гиперболы параллельны координатным осям Ox и Oy , то ее уравнение имеет вид
79
(x − x0 )2 |
− |
(y − y0 )2 |
=1 или |
(y − y0 )2 |
− |
(x − x0 )2 |
=1, |
|
a2 |
b2 |
|||||||
a2 |
|
b2 |
|
|
|
где x0 и y0 – координаты центра гиперболы.
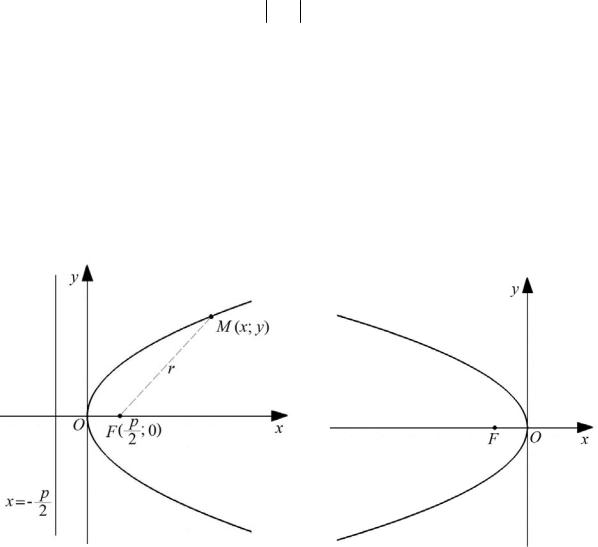
Определение 3.7. Параболой называется геометрическое место точек, равноудаленных от некоторой точки плоскости, называемой фокусом, и некоторой прямой, называемой директрисой.
В системе координат, у которой положительная полуось абсцисс проходит через фокус параболы перпендикулярно директрисе и начало координат лежит на параболе (рис. 3.19), уравнение параболы имеет вид
y2 = 2 px |
(3.24) |
и называется каноническим уравнением параболы.
Здесь р ( p > 0 ) – расстояние от фокуса F до директрисы, называемое па-
раметром параболы. Отрезок r = MF – фокальный радиус точки M (x; y), ле-
жащей на параболе. Уравнения
y2 = −2 px , x2 = −2 py и x2 = 2 py (p > 0)
также определяют параболы, вид которых изображен на рис. 3.20 – 3.22.
Если ось симметрии параболы параллельна оси абсцисс или оси ординат, то уравнение параболы имеет вид
(y − y0 )2 = ±2 p(x − x0 ) или (x − x0 )2 = ±2 p(y − y0 ),
где x0 и y0 координаты вершины параболы.
Рис. 3.19 |
Рис. 3.20 |
80
