Методическое пособие 519

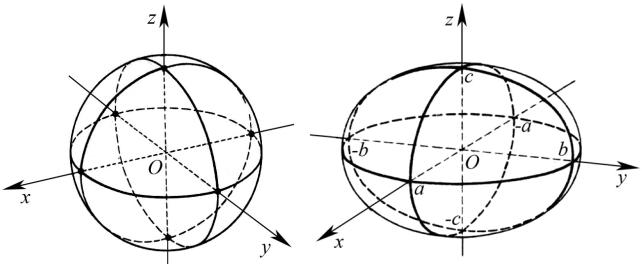
Каноническое уравнение эллипсоида имеет вид

где а, b и с – полуоси эллипсоида (рис. 3.41).

Если все полуоси эллипсоида различны, то его называют трехосным.

Различают два вида гиперболоидов: однополостный и двуполостный. Каноническое уравнение однополостного гиперболоида (рис. 3.42) имеет

вид

Каноническое уравнение двуполостного гиперболоида (рис. 3.43) имеет

вид

Различают два вида параболоидов: эллиптический и гиперболический. Каноническое уравнение эллиптического параболоида (рис. 3.44) имеет

вид

где p q > 0 .

91

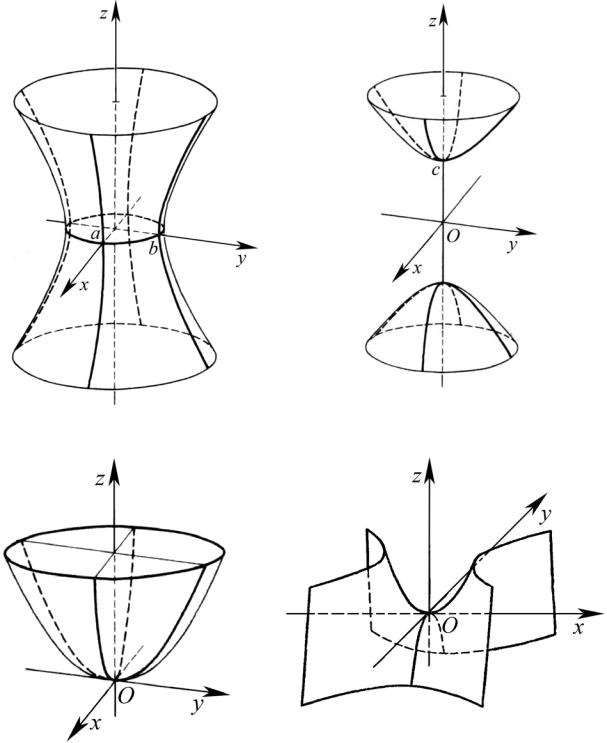
Каноническое уравнение гиперболического параболоида (рис. 3.45) имеет

вид

где p q > 0 .

92

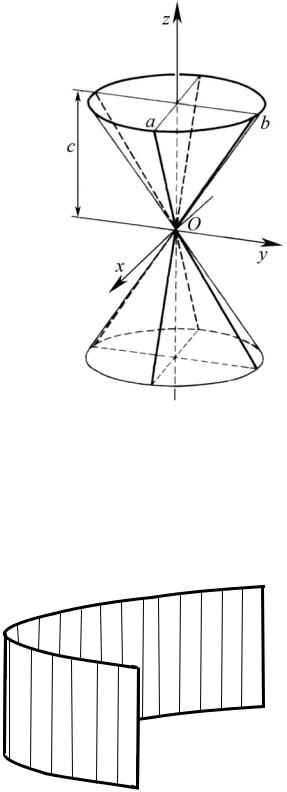
Каноническое уравнение конуса (конической поверхности) (рис. 3.46)

Рис. 3.46

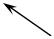
Определение 3.9. Цилиндрической поверхностью, или цилиндром, назы-

вается поверхность, образованная движением прямой L, которая перемещается в пространстве параллельно самой себе, пересекая некоторую кривую K (рис. 3.47). При этом кривая K называется направляющей цилиндра, а прямая L

– его образующей.

L

К

Рис. 3.47

93

Если направляющая цилиндрической поверхности лежит в координатной плоскости, а образующие перпендикулярны этой плоскости, то уравнение этой поверхности совпадает с уравнением ее направляющей.

Если направляющая – это линия второго порядка, то цилиндрическая поверхность – это поверхность второго порядка, название которой порождается названием направляющей.

Например, если направляющей служит эллипс в плоскости xOy

то соответствующая цилиндрическая поверхность называется эллиптическим цилиндром (рис. 3.48), который описывается уравнением (3.48).

Частным случаем (при a =b ) эллиптического цилиндра является круговой цилиндр. Его уравнение имеет вид

x2 + y2 = R2 ,

где R = a .

то соответствующая цилиндрическая поверхность называется параболическим цилиндром (рис. 3.50), а уравнение (3.51) описывает этот цилиндр.

y

M (x; y)

R = K1

Рис. 3.51

3.2.Тестовые задания и их решение

3.2.1.Основные задачи аналитической геометрии на плоскости

Втестовых заданиях 3.1 и 3.2 рассматриваются точки на числовой оси, имеющие одну координату.

Тестовое задание 3.1

Решение. Первый и третий ответы верные. Второй ответ очевидно неверен, так как по разные стороны от начала координат лежат точки, имеющие координаты разных знаков. Четвертый ответ неверен, так как координаты точки равны расстоянию от этой точки до начала отсчета, взятому со знаком «+» или «–» в зависимости от того, по какую сторону от начала отсчета лежит эта точка, т.е. есть две точки, лежащие на фиксированном расстоянии d от начала отсчета, их координаты равны d и −d .

Тестовое задание 3.2

Решение. Так как координаты точек уменьшаются при движении точек по числовой оси в направлении противоположном направлению оси и (a − 2)< a , то третье утверждение верно. Так как расстояние между точками

A(x1 ) и B (x2 ) равно модулю разности координат точек, т.е. AB = x2 − x1 , то верно четвертое утверждение NM = a −(a − 2) = 2 .

По условию a < 0 , а значит, (a − 2)< 0 – обе точки лежат по одну сторо-

ну от начала координат. Делаем вывод, что первое утверждение неверно. Второе утверждение тоже неверно, так как расстояние от точки M (a) до начала

отсчета равно a , а от точки N (a − 2)= a + 2 (a < a + 2).

При решении тестовых заданиях 3.3 – 3.9 используются формулы (3.2′) определения координат середины отрезка.

97

Решение. Если точка M (x; y) симметрична точке B(−2;6) относительно точки A(2;−4), то это означает, что точка А – середина отрезка ВМ. По форму-

ле (3.2′)

т.е.

xM = 2xA − xB , yM = 2 yA − yB .

Имеем

xM = 2 2 + 2 = 6 , yM = 2 (−4)−6 = −14 ,

т.е. верным является первый ответ.

Можно было не находить координаты точки M (x; y), а, вычисляя полу-

суммы координат точки В и предлагаемых точек М, сверять их с координатами точки А.

Тестовое задание 3.4

Если точка A(7; 1) – начало отрезка 2

АВ и M (5; 0) – его середина, то сумма координат точки В равна …

Решение. В этой задаче точка M (x; y) – середина отрезка АВ, поэтому по формуле (3.2′)

поэтому, складывая эти равенства, имеем

xB + yB = 2(xM + yM )−(xA + yA )= 2(5 + 0)−(7 +1)= 2 .

Ответ: 2.

98

Тестовое задание 3.8

Точки A(2; −6), B(4; −2) и C (8; −2) 1

являются последовательными вершинами параллелограмма. Тогда сумма координат точки пересечения диагоналей равна…

Решение. По условию А, В, С – последовательные вершины параллелограмма, поэтому А и С являются противоположными вершинами, т.е. концами одной диагонали. Как известно, диагонали в точке пересечения делятся пополам, поэтому эта точка является серединой отрезка АС. Найдем ее координаты (x; y) по формулам (3.2′):

x = xA +2 xC = 2 +2 8 = 5 , y = yA +2 yC = −62− 2 = −4 ,

откуда x + y = 5 − 4 =1. Ответ: 1.

Верен второй ответ.

При решении тестовых заданиях 3.10 – 3.16 используется формула (3.1) расстояния между двумя точками.

Тестовое задание 3.10

100