
Методическое пособие 519
.pdf
Рис. 3.21 |
Рис. 3.22 |
3.1.5. Прямая и плоскость в пространстве
Плоскость в пространстве
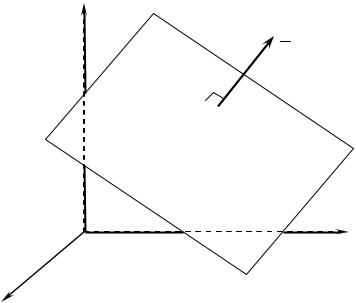
Рассмотрим в пространстве прямоугольную систему координат xOyz . Уравнение плоскости Q, проходящей через заданную точку M0 (x0; y0; z0 ) перпендикулярно вектору N {A; B;C} (рис. 3.23) имеет вид
A(x − x0 )+ B(y − y0 )+C (z − z0 )= 0 |
(3.25) |
и называется уравнением плоскости, проходящей через данную точку M0 (x0; y0; z0 ) перпендикулярно нормальному вектору N {A; B;C}.
Если N {A; B;C} – нормальный вектор плоскости, то уравнение такой плоскости – это линейное уравнение вида
Ax + By +Cz + D = 0 , |
(3.26) |
называемое общим уравнением плоскости.
81
z
Q
N {A; B; C}
 M 0 (x0 ; y0 ; z0 )
M 0 (x0 ; y0 ; z0 )
O |
y |
x
Рис. 3.23
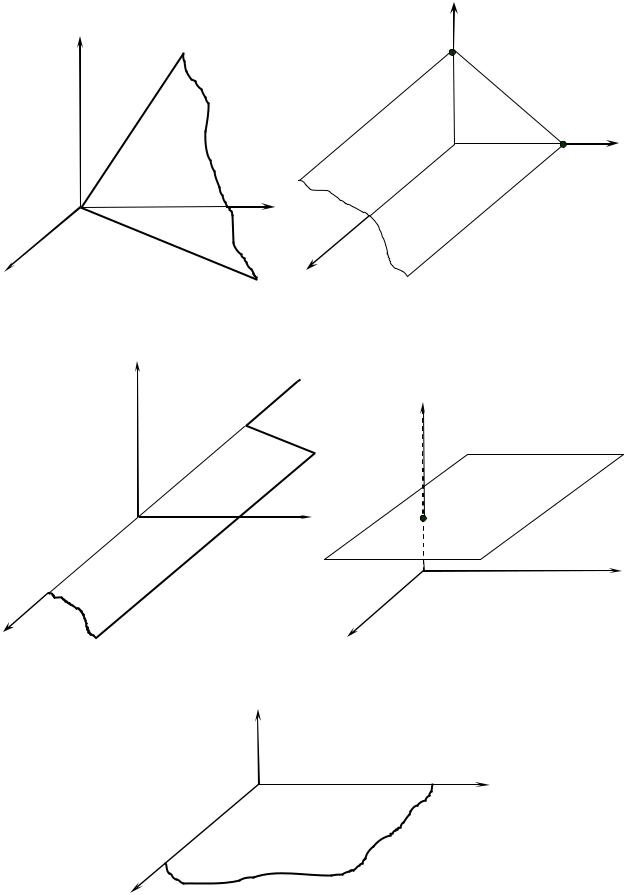
А. Если D = 0 , т.е. уравнение плоскости имеет вид Ax + By +Cz = 0 , то
плоскость Q проходит через начало координат (рис 3.24).
Б. Если A = 0 , т.е. уравнение плоскости имеет вид By +Cz + D = 0 , то
плоскость Q перпендикулярна плоскости yOz или, что тоже самое, плос-
кость Q параллельна оси Ox (рис 3.25). Можно сделать вывод: если в уравне-
нии плоскости отсутствует какая-нибудь переменная, то плоскость будет параллельна координатной оси того же названия, что и отсутствующая переменная.
В. Если |
A = D = 0 , то плоскость By +Cz = 0 |
проходит через ось Ox |
||
(рис. 3.26). Аналогично уравнения Ax +Cz = 0 (при |
B = D = 0 ) и Ax + By = 0 |
|||
(при C = D = 0 ) описывают плоскости, проходящие соответственно через оси |
||||
Oy и Oz . |
|
|
|
|
Г. Если |
A = B = 0 , то плоскость Q |
параллельна плоскости |
xOy |
|
(рис. 3.27). Аналогично, уравнения Ax + D = 0 |
(при B =C = 0 ) и By + D = 0 (при |
|||
A =C = 0 ) задают плоскости, соответственно параллельные плоскостям |
yOz и |
|||
xOz .
Д. Если A = B = D = 0 , то плоскость имеет уравнение z = 0 , т.е. плос-
кость Q – это координатная плоскость xOy (рис. 3.28). Аналогично плоско-
сти y = 0 и x = 0 – это плоскости xOz и yOz соответственно.
82
z
z
Q
O
y
O
y
Q
x
Рис. 3.24 |
Рис. 3.25 |
z
z
Q
y |
z = − |
D |
C |
||
O |
|
|
|
O |
|
y
Q
x
Рис. 3.26 |
Рис. 3.27 |
z
O
y
Q
x
Рис. 3.28
83
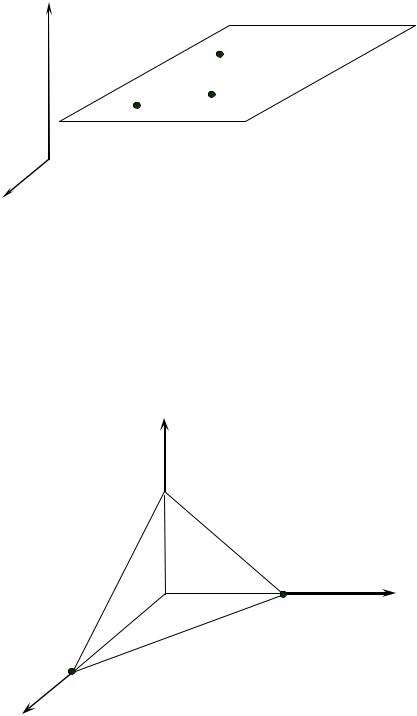
Уравнение |
плоскости, |
проходящей |
через три заданные |
точки |
||||
M1 (x1; y1; z1 ), M2 |
(x2; y2; z2 ) и |
M3 (x3; y3; z3 ), не лежащие на одной прямой |
||||||
(рис. 3.29), имеет вид |
|
|
|
|
|
|
||
|
|
x − x1 |
y − y1 |
z − z1 |
|
|
|
|
|
|
|
|
|||||
|
|
x2 − x1 |
y2 − y1 |
z2 − z1 |
|
= 0 . |
(3.27) |
|
|
|
x3 − x1 |
y3 − y1 |
z3 − z1 |
|
|
|
|
z |
|
|
|
|
Q |
|
||
|
|
|
|
M 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M 3 |
M 2 |
|
|
|
|
O  y
y
x
Рис. 3.29
Если плоскость отсекает на осях Ox , Oy и Oz соответственно отрезки а,
b и с не равные нулю, т.е. проходит через три точки |
A(a;0;0), B(0;b;0) и |
||||||
C (0;0;c) (рис. 3.30), то уравнение плоскости имеет вид |
|
||||||
|
x |
+ |
y |
+ |
z |
=1 |
(3.28) |
|
a |
b |
|
||||
|
|
|
c |
|
|||
и называется уравнением плоскости в отрезках на осях. z
 C (0; 0; c )
C (0; 0; c )
Q
O
B (0; b; 0 ) y
A (a; 0; 0 )
x
Рис. 3.30
84
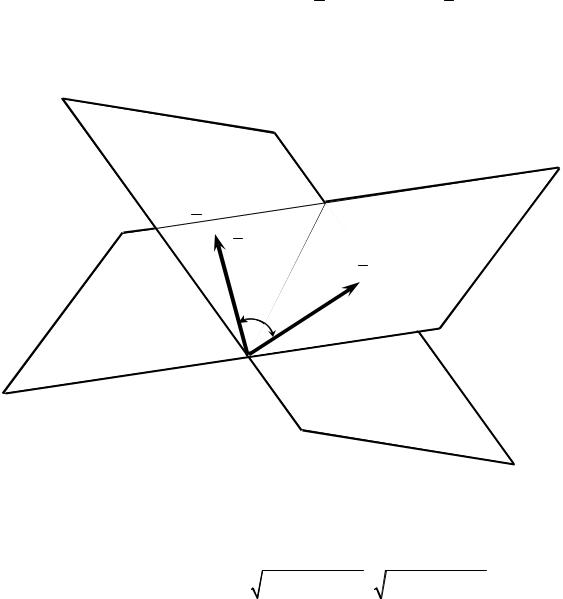
Угол между двумя плоскостями.
Условия параллельности и перпендикулярности плоскостей
Если известны нормальные векторы N1{A1; B1;C1} и N2 {A2; B2;C2} плоскостей Q1 и Q2 , угол ϕ между нормальными векторами равен одному из углов
между плоскостями (рис. 3.31).
Q1
N1 {A1; B1; C1}
N1
N 2 N 2 {A2 ; B2 ; C2 }
ϕ
ϕ
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.31 |
|
|
|
|
Поэтому косинус угла между плоскостями можно найти по формуле |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1A2 + B1B2 +C1C2 |
|
|
|
cosϕ = |
|
|
N |
1 |
|
|
|
N2 |
|
|
= |
|
|
. |
(3.29) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
N1 |
|
|
|
N2 |
|
|
|
|
A12 + B12 +C12 A22 + B22 |
+C22 |
|
|||||||||
|
|
|
|
|
|
|||||||||||||||||
Условие перпендикулярности двух плоскостей имеет вид |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
A1A2 + B1B2 +C1C2 = 0 , |
|
|
(3.30) |
|||||||
а условие параллельности двух плоскостей –
A1 |
= |
|
B1 |
= |
C1 |
. |
(3.31) |
|
A |
B |
|
||||||
|
|
|
C |
2 |
|
|
||
2 |
|
2 |
|
|
|
|
||
|
|
85 |
|
|
|
|
|
|
Расстояние от точки до плоскости
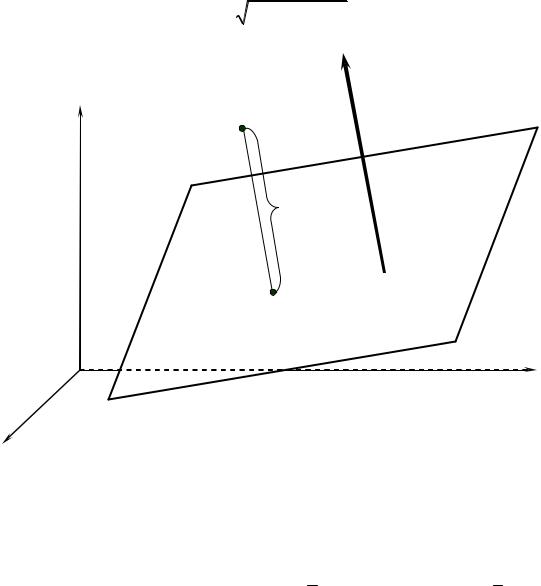
Если задана точка M0 (x0; y0; z0 ) и плоскость Q общим уравнением
Ax + By +Cz + D = 0 и (рис. 3.32), то расстояние d от точки M0 |
до плоскости Q |
|||||||||
вычисляется по формуле |
|
|
|
|
|
|
|
|
|
|
|
d = |
|
|
Ax0 + By0 +Cz0 + D |
|
|
. |
(3.32) |
||
|
|
|
||||||||
|
|
|
||||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
A2 + B2 +C2 |
|
|||||
|
|
|
|
|
|
{A; B;C} |
|
|||
|
|
|
|
N |
|
|||||
z |
M0 (x0; y0; z0 ) |
|
||||||||
d
Q
O
y
x
Рис. 3.32
Прямая линия в пространстве
Если известны направляющий вектор S {m; n; p} прямой L ( S & L ) и точка M0 (x0 ; y0 ; z0 ), лежащая на L (рис. 3.33), то уравнения прямой имеют вид
x − x0 |
= |
y − y0 |
= |
z − z0 |
(3.33) |
|
m |
n |
p |
||||
|
|
|
и называются каноническими уравнениями прямой в пространстве. 86

z
L
M 0 (x0 ; y0 ; z0 ) |
|
{m; n; p} |
S |
O |
|
y |
|
|
x |
|
|
|
|
Рис. 3.33 |
|
|||
Эту же прямую можно задать параметрическими уравнениями: |
|
|||
x = x0 +tm, |
|
|||
|
+tn, |
(3.34) |
||
y = y0 |
||||
|
+t p, |
|
||
z = z0 |
|
|||
где t – параметр ( −∞ <t < ∞).
Уравнения прямой, проходящей через две заданные точки M1 (x1; y1; z1 ) и
M2 (x2 ; y2 ; z2 ) (рис. 3.34), имеют вид
x − x1 |
= |
y − y1 |
= |
z − z1 |
. |
(3.35) |
|||||
|
|
|
|||||||||
x |
− x |
|
y |
2 |
− y |
|
z |
2 |
− z |
|
|
2 |
1 |
|
|
1 |
|
|
1 |
|
|
||
z
L
M1 (x1; y1; z1 )
M 2 (x2 ; y2 ; z2 )
O |
y |
x
Рис. 3.34
87
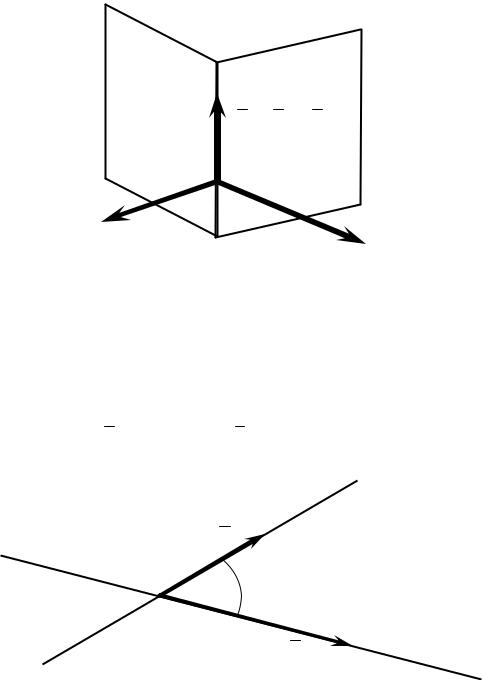
Прямую в пространстве можно задать как линию пересечения двух непараллельных плоскостей Q1 и Q2 (рис. 3.35) системой уравнений этих плоско-
стей:
A x + B y +C z + D =0, |
(3.36) |
|||
1 |
1 |
1 |
1 |
|
A2 x + B2 y +C2 z + D2 =0. |
|
|||
Систему уравнений (3.36) называют общими уравнениями прямой.
Q1
Q2
S = N1 × N 2
|
|
|
|
|
|
N |
|
||||
N |
1 |
2 |
|||
Рис. 3.35
Угол между прямыми в пространстве. Условия параллельности и перпендикулярности прямых
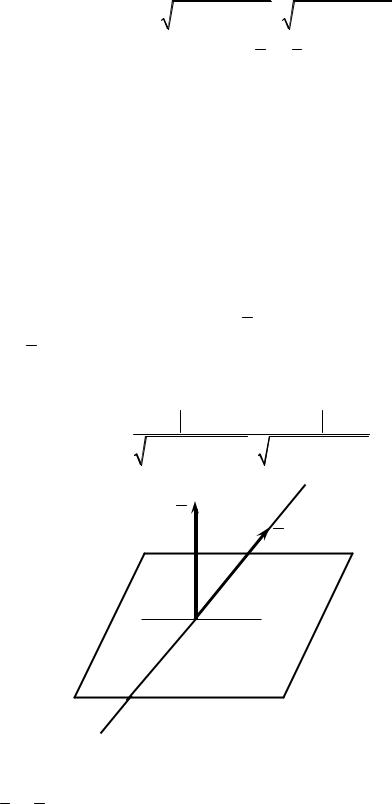
Под углом между прямыми L1 и L2 понимают угол между их направ-
ляющими векторами S1 {m1; n1; p1} и S2 {m2 ; n2 ; p2} (рис. 3.36) (при этом пря-
мые могут и не пересекаться).
L1
S1
ϕ
S2 |
L2 |
|
Рис. 3.36
88
Косинус угла между прямыми L1 и L2 находят по формуле
|
|
|
|
|
|
|
|
|
|
|
|
|
m1 m2 + n1 n2 + p1 p2 |
|
|
|
||||||
cosϕ = |
|
S |
1 |
|
S2 |
= |
|
. |
(3.37) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
S1 |
|
S2 |
|
m2 |
+ n2 |
+ p2 |
|
m2 |
+ n2 |
+ p2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
2 |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Условие перпендикулярности прямых ( S1 S2 ) имеет вид m1 m2 + n1 n2 + p1 p2 = 0 ,
а условие параллельности ( |
|
|
|
|
|
|
|
|
|
|
S1 & S2 ) – |
|
|
|
|
|
|||||
|
|
|
|
|
m1 |
= |
n1 |
= |
p1 |
. |
|
|
|
|
|
m |
n |
|
|||
|
|
|
|
|
|
|
p |
|||
2 |
2 |
|
2 |
|
||||||
Угол между прямой и плоскостью.
Условия параллельности и перпендикулярности прямой и плоскости
Если известны нормальный вектор N{A; B; C} плоскости Q и направляющий вектор S{m; n; p} прямой L (рис. 3.37), то можно найти синус угла ϕ между прямой L и плоскостью Q по формуле
sinϕ = |
A m + B n +C p |
|
A2 + B2 +C2 m2 + n2 + p2 . |
(3.38) |
L
N
S
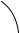 ϕ
ϕ
Q
Рис. 3.37
Условие параллельности прямой и плоскости (принадлежности прямой и плоскости) ( N S (рис. 3.38)) имеет вид
A m + B n +C p = 0 , |
(3.39) |
89
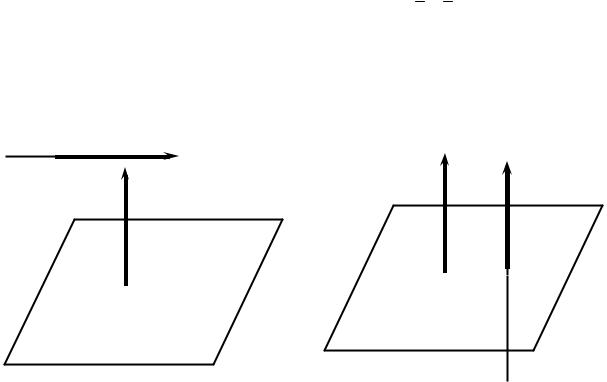
а условие перпендикулярности прямой и плоскости ( N & S (рис. 3.39)) –
|
|
|
|
|
|
|
A |
= |
B |
= C . |
|
|
(3.40) |
|||
|
|
|
|
|
|
|
m |
n |
|
|
||||||
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
||
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|||||
|
|
N |
|
|
|
|||||||||||
|
|
|
|
|
|
|
||||||||||
Q
Q
Рис. 3.38 |
Рис. 3.39 |
3.1.6. Поверхности второго порядка
Поверхностями второго порядка являются: сфера, эллипсоид, однополостный и двуполостный гиперболоиды, эллиптический и гиперболический параболоиды, конус, а также эллиптический, гиперболический и параболический ци-
линдры.
Определение 3.8. Сферой называется геометрическое место точек пространства, находящихся на одинаковом расстоянии R (радиуса сферы) от данной точки (центра сферы).
Уравнение, определяющее |
сферу |
радиуса |
R с центром |
в точке |
||||
M0 (x0; y0; z0 ), имеет вид |
|
|
|
|
|
|
|
|
(x − x |
)2 +(y − y |
)2 |
+(z − z |
0 |
)2 |
= R2 . |
(3.41) |
|
0 |
|
0 |
|
|
|
|
|
|
Если центр сферы совпадает с началом координат (рис. 3.40), то уравнение сферы принимает вид
x2 + y2 + z2 = R2 . |
(3.42) |
90
