Методическое пособие 519

Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

, могут быть найдены

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

2.01 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 167 8 9 10 11 12 13 14 15 16 > Следующая >>>

Решение. Методом Крамера можно решить систему, матрица которой квадратная и невырожденная. Неизвестные находятся по формулам (2.20), где - определитель матрицы системы, а j определяются по формулам (2.21). У

нас

−5

поэтому

−5

= −6

−(−15)=9,

A =

−3

1 =

−5

= −12 −(−35)= 23 ,

2 =

14 −12 = 2 .

Итак

=9 , 1 = 23,

−3

2 = 2 .

Тестовое задание 2.35

Пусть A и B – обратимые квадратные

1 A−1B

матрицы одного порядка. Тогда реше-

нием матричного уравнения

3XA = B

является матрица…

−1

3 BA

3A−1B

3BA−1

Решение. В этом задании нужно из уравнения

3XA = B

выразить X .

Сначала умножим обе части уравнения на

1 ,

получим

XA =

1 B . По условию

матрица A обратима, т.е. существует A−1 . Умножим левую и правую части по-

лучившегося уравнения справа на A	−1	. Получим	(XA)A	−1		1		−1	или, учи-
лучившегося уравнения справа на A		. Получим	(XA)A		=		B A		или, учи-
					3

тывая свойства умножения матриц, имеем X (AA−1 )= 13 (BA−1 ). Так как AA−1 = I

и X I = X , получаем X = 13 BA−1 , что соответствует второму ответу.

Тестовое задание 2.36

При решении системы линейных уравнений с квадратной матрицей коэффициентов A можно применять формулы Крамера, если

одно из уравнений системы является линейной комбинацией остальных

ранг матрицы A равен числу ее неизвестных

определитель матрицы A отличен от нуля столбец свободных членов является ненулевым

Решение. Вспомним, что формулы Крамера применимы, если матрица A системы квадратная и det A ≠ 0 , в этом случае система имеет единственное решение. Проанализируем предлагаемые ответы.

Первый ответ неверен, так как если одно из уравнений является линейной комбинацией остальных, то вектор-строка расширенной матрицы системы является линейной комбинацией остальных векторов-строк, из чего следует, что векторы-строки линейно зависимы. По определению 2.13′ делаем вывод, что ранг расширенной матрицы системы меньше числа уравнений, а значит, и ранг матрицы системы меньше числа уравнений, т.е. определитель матрицы системы равен нулю – метод Крамера не применим.

Второй ответ верный, т.к условие равенства ранга квадратной матрицы системы числу неизвестных означает ее невырожденность ( det A ≠ 0 ).

Третий ответ верен, матрица системы невырождена.

Четвертый ответ неверен, т.к. столбец свободных членов не связан со значением главного определителя системы.

Ответ: верны второе и третье утверждения.

Тестовое задание 2.37

При решении системы линейных уравнений с квадратной матрицей коэффициентов A нельзя применять формулы Крамера, если

ни одна из строк матрицы A не является линейной комбинацией остальных

столбцы матрицы A линейно независимы

определитель матрицы A равен нулю

строки матрицы A линейно зависимы

Решение. Учитывая рассуждения, проведенные при обсуждении предыдущего задания, делаем вывод, что формулы Крамера нельзя применять, если определитель квадратной матрицы системы равен нулю. Обсудим предлагаемые утверждения. Те утверждения, из которых следует, что det A = 0 ( A - матрица системы), верны.

Первое утверждение неверно, т.к. из него следует, что векторы – строки матрицы системы линейно независимы, т.е. ее ранг равен числу уравнений, а значит числу неизвестных, т.е det A ≠ 0 .

Второе утверждение тоже неверно, т.к. в этом случае по определению 2.13′ ранг матрицы системы равен количеству всех ее столбцов, т.е. det A ≠ 0 .

Третье утверждение, как уже обсуждалось, верно.

Четвертое утверждение тоже верно, т.к. линейная зависимость строк матрицы A по определению 2.13′ говорит о том, что ранг A меньше числа уравнений, поэтому det A = 0 .

Ответ: верны третье и четвертое утверждения.

Тестовое задание 2.38

Дана система линейных уравнений

−2

αx −3y = 2,

0,5

4x −6 y = 2.

Система не имеет решений при α

равном…

Решение. Система

не

имеет решений, если

r( A) ≠ r(

) . У нас

α −3

α −3 2

A =

−6 2

. У матрицы

A есть минор второго порядка, от-

4 −6

личный от

нуля.

Он

соответствует

второму и

третьему столбцам:

−3

= −6 −

(−12)= 6 ≠ 0 . Значит, r(

) = 2 . Система не будет иметь решения,

−6

если r( A) ≠ 2 , т.е. det A = 0 , т.к. матрица A имеет лишь один минор второго по-

рядка - det A . Так как det A =	α	−3	= −6α +12, то, если −6α +12 = 0 , т.е. при
рядка - det A . Так как det A =	α	−3	= −6α +12, то, если −6α +12 = 0 , т.е. при
	4	−6

α = 2 , система не имеет решений.

Можно было решить это задание, эквивалентно преобразовав систему. Действительно, разделим обе части второго уравнения системы на 2 и вычтем

из первого уравнения второе. Имеем
αx −3y = 2,		αx −3y = 2,	~	(α −2)x =1,
	−6 y = 2.	~	~
4x	−6 y = 2.	2x −3y =1.		2x −3y =1.
При (α −2)= 0	первое уравнение не имеет решений, т.е. при α = 2 сис-

тема несовместна. При α ≠ 2 , очевидно, система имеет решение, т.к. ее опреде-

литель =	α −2	0	= −3(α −2)≠ 0 .
литель =	α −2	0	= −3(α −2)≠ 0 .
	2	−3
Ответ: α = 2 .
Тестовое задание 2.39
3x +αy = 0					α = ±3
3x +αy = 0
Система				имеет ненулевое
x +3y = 0.					α =9
решение при…					α = 0
					α = −9

Решение. В этом задании дана всегда совместная однородная система, имеющая единственное нулевое решение, если ее определитель не равен нулю,

т.е. =	3	α	≠ 0 . В противном случае, т.е. при условии =9 −α = 0	(α =9),

	1	3

система имеет множество решений, т.е. имеет ненулевые решения. Ответ: α =9 .

Тестовое задание 2.40

Если (x0 ; y0 ) – решение системы линейных уравнений

x −5y = 2

−2x +3y = 4 ,

то x0 может определяться по формуле…

				−5	2
				−5	2
x	=			3	4
				3	4

		1			−5
0		1			−5
		−2			3
		1			−5
		1			−5
x	=	−2			3
		−2			3
				2	−5
0				2	−5
				4	3
			1		2
			1		2
x	=			−2	4
				−2	4
		1			−5
0		1			−5
		−2			3
				2	−5
				2	−5
x	=			4	3
				4	3

		1			−5
0		1			−5
		−2			3

Решение. Так как в предложенных ответах значение x0 выражается через определители и учитывая, что главный определитель системы не равен нулю:

1 −5

=3 −10 = −7 ≠ 0 ,

−2 3

делаем вывод, что система имеет единственное решение (x0 ;

y0 ), а значение x0

можно найти, используя метод Крамера, по формуле x = 1

, где

−5

Иными словами,

		2	−5
		2	−5
x =		4	3		,

	1		−5
0	1		−5
0
	−2		3
что соответствует четвертому ответу.
Тестовое задание 2.41
Если (x0 ; y0 ) – решение системы ли-					−1,5
Если (x0 ; y0 ) – решение системы ли-					−1,5
нейных уравнений				4,5
3x −4 y =15,				4,5
3x −4 y =15,				1,5
x −4 y =9,					−4,5
тогда x0 + y0 равно…

Решение. В этом задании нужно решить систему, а затем сложить найденные значения неизвестных. Решим систему с помощью метода Гаусса:

3x − 4 y =15,	~	(3x − x)−4 y + 4 y =15 −9,	~	2x = 6,			~	x =3,	~
					−4 y	=9.
x − 4 y = 9.		x −4 y =9.		x				x −4 y =9.

~	x =3,		~	x =3,	~	x =3,
		−4 y =9.
	3			4 y = −6.		y = −1,5.
Итак, x0 =3, y0 = −1,5 , значит,				x0 + y0 =3 −1,5 =1,5 .
Ответ: x0 + y0 =1,5 .

2.2.9. Собственные векторы и собственные значения матрицы

Тестовое задание 2.42
	4						6
	4
Вектор X =	1	является собственным
Вектор X =		является собственным					−5
							−5
				5	4		−6
вектором матрицы			A =	1	2	. Тогда	1

соответствующее собственное значение равно…

Решение. Собственный вектор X ответствующий собственному значению нию AX = λX , т.е. для данной матрицы X выполняется равенство

матрицы A (см. определение 2.21), со- λ , удовлетворяет матричному уравне- A и известного собственного вектора

		5	4		4		4		5	4	4		4
	AX =		2	= λX = λ				, т.е.	1	= λ
		1	2		1		1		1	2	1		1
				5 4 + 4 1		4λ		24 4λ				,
		или		1	=	λ	, т.е.		6	=	λ	,
				1	4 + 2 1	λ			6		λ
4λ =	24	, т.е. λ =		6 (первый ответ).
откуда		, т.е. λ =		6 (первый ответ).
λ = 6

Тестовое задание 2.43

Собственные значения собственных векторов линейного преобразования, заданного в некотором базисе матри-

по формуле…

2	−λ	4		= 0

	1	3 −λ
2	+λ	4			= 0

	1	3 +λ
	2	4 −λ	= 0

1 −λ		3
	2	4 +λ	= 0

1 +λ		3

Решение. Уравнение для отыскания собственных значений линейного преобразования составляется по матрице этого преобразования, соответствующей какому-нибудь базису линейного пространства, по формуле (2.23). В этой формуле стоит определитель, полученный из определителя матрицы преобразования вычитанием из диагональных элементов искомого неизвестного собст-

	2	4	, поэтому искомое уравнение
венного значения λ . В нашем задании A =	1	3	, поэтому искомое уравнение
	1	3

записано в первом ответе – первый ответ верен.

Тестовое задание 2.44

Вектор

X =

собствен-

−1

является

−3

1,5

ным вектором матрицы A ,

соответст-

−4

вующий

собственному

значению

λ = −2. Тогда произведение

A X рав-

но…

−5

−1

Решение. Если X – собственный вектор матрицы

A , соответствующий

собственному значению λ , то справедливо равенство AX = λX . У нас λ = −2 ,

−4

- второй ответ.

X =

−3

, поэтому AX = −2

−3

2.2.10. Квадратичные формы

Тестовое задание 2.45

10x

−9xy +10 y

Матрице

3 5

соответствует

квад-

2x2 +3xy +5y2

ратичная форма …

2x2 −9xy +5y2

2x2 +6xy +5y2

Решение. В п. 2.1.5 объяснялось, как ищется матрица A квадратичной формы: ее элементы aij - это коэффициенты при произведениях переменных

xi xj , причем считается, что коэффициенты при произведениях xi xj и xj xi рав-

ны, т.е. A симметричная матрица. В предлагаемых вариантах ответа даны квадратичные формы относительно переменных x и y . Будем считать, что x -

это x1 , а y - это x2 . В данной матрице квадратичной формы a11 = 2 , т.е. коэф-

фициент

при

x x = x2 = x2

равен

двум;

a =5 , т.е.

коэффициент при

= x2

= y2

равен

пяти;

= a

=3, т.е.

коэффициент

при x x

= xy и

x2 x1 = yx равен трем. Полученная квадратичная форма имеет вид

2x2 +5y2 +3xy +3yx , т.е. 2x2 +6xy +5y2

- четвертый ответ верный.

Тестовое задание 2.46

Квадратичная форма 7x2	−12x x	+λx2	−6
1	1 2	2	−6
является положительно определенной			5
при λ равном…			3
			6

Решение. Воспользуемся критерием Сильвестра, сформулированным в п. 2.1.5, являющимся критерием положительной определенности квадратичной формы. Найдем матрицу квадратичной формы и главные миноры этой матрицы. Условие их положительности обеспечит положительную определенность данной квадратичной формы. По определению: a11 – это коэффициент при

x x = x2			( a = 7 ), a	22	– это коэффициент при							x	x	= x2	( a = λ),	a = a	21	-
1	1	1	11	22							2		2	2	22	12	21
это половина коэффициента при x1 x2								( a12 = −6). Итак,
								7	−6
							A =	−6	λ	.
								−6	λ
	Главные миноры матрицы A - это
			M1 =			7	= 7 и M 2 =		7	−6		= 7λ −36 .


									−6 λ
									−6 λ
	Если M1 и M2 положительны, то данная квадратичная форма положи-
тельно		определена.			Очевидно, M1 = 7 > 0 ,							если		M 2 = 7λ −36 > 0 ,			т.е.
λ >	36	=5	1 , то квадратичная форма положительно определена. Из предложен-
	7		7							1 .
ных вариантов нам подходит λ = 6 , т.к. 6 >5										1 .
										7

Ответ: λ = 6 .

3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ. ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ

3.1.Краткие теоретические сведения

3.1.1.Основные задачи аналитической геометрии на плоскости

Рассмотрим на плоскости прямоугольную систему координат xOy . К ос-

новным (простейшим) задачам аналитической геометрии на плоскости относят три задачи.

Задача 1. Нахождение расстояния между двумя точками.

Расстояние d между точками A(x1; y1 ) и B(x2 ; y2 ) плоскости Oxy находится по формуле

	d =	AB	= (x	− x )2	+(y	2	− y )2 .		(3.1)
	d =	AB	= (x	− x )2	+(y		− y )2 .		(3.1)
			2	1			1
	Задача 2. Деление отрезка в данном отношении.
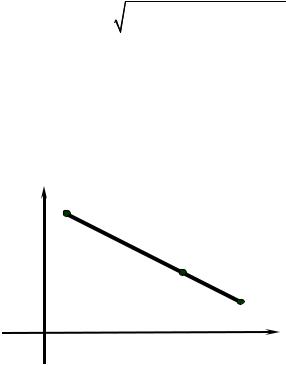
	Определяются координаты точки M (x; y), которая делит отрезок								AB ,
соединяющий точки A(x1; y1 ) и B(x2 ; y2 )					в заданном отношении			λ > 0	, т.е.
AM	= λ (рис. 3.1).
MB
	у	A (x1 ; y1 )

			M (x; y )
				B (x2 ; y2 )
О				х
	Рис. 3.1
Справедливы формулы
x =	x1 +λx2	и	y =	y1 +λy2	.	(3.2)
	1 +λ
				1 +λ

Если M (x; y)–середина отрезка AB , то λ =1 и формулы (3.2) примут вид

x =	x1 + x2	и	y =	y1 + y2	.	(3.2′)

2			2

Задача 3. Вычисление площади треугольника.								A(x1; y1 ),
Площадь S треугольника,				вершины		которого – точки
B(x2 ; y2 ), C (x3 ; y3 ), находится по формуле
1			(x2 − x1 ) (y2 − y1 )

S =		\|	(x	− x )	(y	− y )	\|.	(3.3)
	2
			3	1	3	1

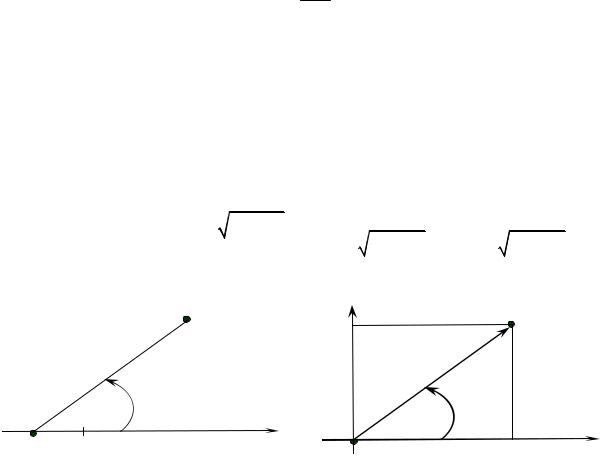
3.1.2. Полярная система координат

Полярная система координат задается точкой О, называемой полюсом, лучом Op , называемым полярной осью, на которой указана единица масштаба.

Положение на плоскости точки М, не совпадающей с полюсом О, определяется двумя числами: ее расстоянием r от полюса О и углом ϕ , где ϕ - это

угол между полярной осью и вектором OM (рис. 3.2).

Числа r и ϕ называются полярными координатами точки М, при этом r

называют полярным радиусом, ϕ – полярным углом. Значения,	принимаемые
полярными координатами, находятся в промежутках: 0 ≤ r < ∞	и 0 ≤ϕ < 2π

(или −π <ϕ ≤π ).

Если совместить начало декартовой системы координат с полюсом, полярную ось с осью Ox (рис. 3.3), то прямоугольные координаты x, y и поляр-

ные координаты r, ϕ точки М будут связаны формулами:

x = r cosϕ , y = r sinϕ , r = x2 + y2 , cosϕ =		x	, sinϕ =	y	. (3.4)
	x2	+ y2		x2 + y2

	у	M
	r	r
		r
	ϕ	ϕ
		ϕ
О 1	p	х
О 1	p	p
	О

Рис. 3.2	Рис. 3.3

<<< < Предыдущая 1 2 3 4 5 67 / 167 8 9 10 11 12 13 14 15 16 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.20221.99 Mб9Методическое пособие 514.pdf
#
30.04.20221.99 Mб11Методическое пособие 515.pdf
#
30.04.20221.99 Mб1Методическое пособие 516.pdf
#
30.04.20221.99 Mб8Методическое пособие 517.pdf
#
30.04.20222 Mб3Методическое пособие 518.pdf
#
30.04.20222.01 Mб11Методическое пособие 519.pdf
#
30.04.2022804.35 Кб5Методическое пособие 52.doc
#
30.04.2022317.56 Кб2Методическое пособие 52.pdf
#
30.04.20222.01 Mб5Методическое пособие 520.pdf
#
30.04.20222.03 Mб8Методическое пособие 521.pdf
#
30.04.20222.03 Mб6Методическое пособие 522.pdf