3.3.2.1. Анализ работы разомкнутых смо

Одноканальная СМО с простейшими потоками с неограниченным временем ожидания требований.

Интенсивность поступления требований на обслуживание - , интенсивность потока обслуживания равна . Длительность обслуживания - случайная величина, подчиненная показательному закону распределения. Представим все возможные состояния системы в виде размеченного графа состояний (рис. 3.4.)

Рис. 3.4. Размеченный граф состояний одноканальная СМО с простейшими потоками

Прямоугольники определяют возможные состояния системы, которые имеют следующую интерпретацию:

S₀- канал свободен, в системе нет ни одного требования;

S₁- канал занят, очереди нет;

S₂- канал занят, одна заявка в очереди;

.................................................................

S_n- канал занят, n-1 заявка в очереди;

.................................................................

Каждый прямоугольник количественно оценивается вероятностью состояний P_n. Стрелки указывают направление перехода из состояния в состояние с указанием интенсивности.

Рассмотрим установившийся режим работы СМО, когда основные вероятностные характеристики системы постоянны во времени, например в течение часа. Тогда интенсивности входных и выходных потоков для каждого состояния будут сбалансированы. Эти сбалансированные потоки будут выглядеть так:

Обозначим ρ=λ/μ - приведенная интенсивность входящего потока, представляющая собой среднее число заявок, поступающих на вход СМО за среднее время обслуживания одной заявки.

Из первого уравнения найдем значение P₁:

Из второго уравнения найдем значение P₂:

, используя выражение для P₁, получим:

, и т.д.:

.

Используя очевидное равенство , получим: . Так как <1 и сумма геометрически убывающей прогрессии равна:

. При n , <1:

Таким образом, вероятность простоя канала обслуживания: .

Вероятность того, что в системе находится n требований, определяется по формуле:

Среднее число обслуживаемых требований N_s, находящихся в системе, определяется по формуле: .

Среднее число требований, находящихся в очереди:

Среднее время ожидания заявки: .

Среднее время пребывания заявки в очереди:

Используя полученные выражения можно определить основные параметры функционирования одноканальной разомкнутой СМО с простейшими потоками.

Многоканальная разомкнутая СМО с простейшими потоками и неограниченным временем ожидания. Такая СМО наиболее соответствует действительности. Особенности системы: поток требований ординарный, без последействия и стационарный. Исходными параметрами, характеризующими такую систему, являются: число каналов – N, интенсивность поступления заявок - , интенсивность обслуживания - . В многоканальной СМО следует различать два случая:

1. число требований n,поступивших в систему, меньше количества каналов обслуживания N,то есть все они находятся на обслуживании (0n<N);

2. число требований n,поступивших в систему, больше или равно числу каналов обслуживания N (N n), то есть N требований обслуживаются, а остальные r ожидают в очереди (r=1,2,…,n-N).

Граф функционирования такой системы приведен на рисунке 3.5.

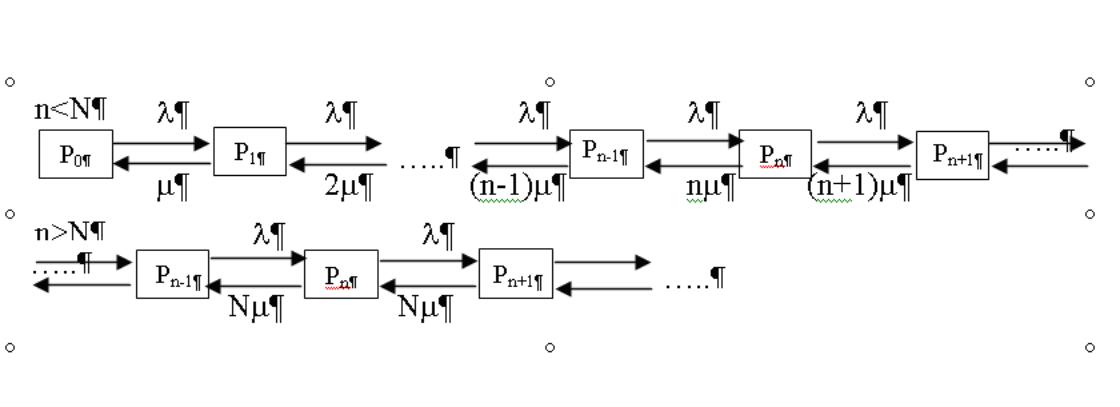
Рис. 3.5. Размеченный граф состояний многоканальной разомкнутой СМО

Ограничимся рассмотрением установившегося режима работы СМО.

Если 0n<N, то:

Если Nn<, то:

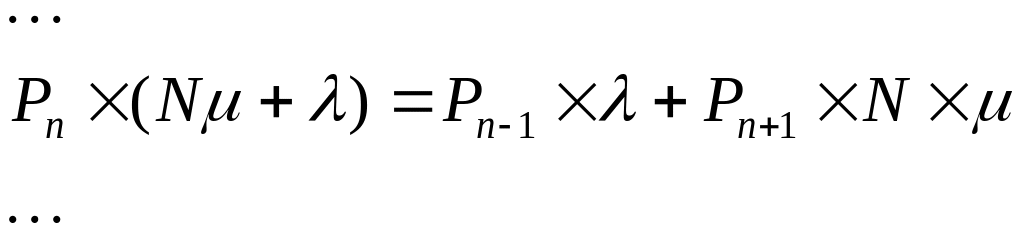
Рассмотрим первый случай, когда 0n<N. Находим из первого уравнения P₁:

Из второго уравнения находим P₂:

Учитывая ранее найденное выражение для P₁, получим: и т.д.

Таким образом, реккурентное выражение для вычисления вероятностей состояний системы для случая n<N имеет вид:

для случая Nn<:

Используя равенство , запишем выражение для P₀:

.

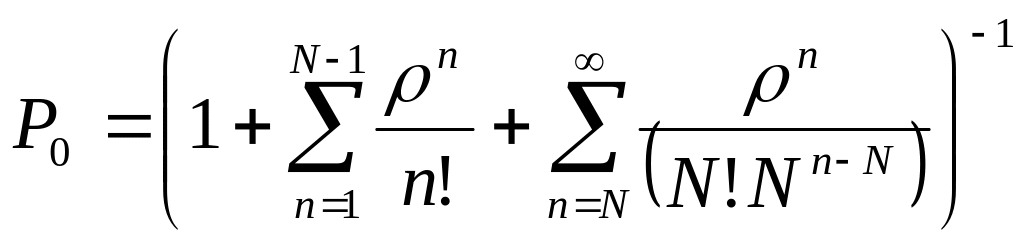Многоканальная разомкнутая СМО с отказами. Для этой СМО характерно полное отсутствие очереди (n = 0), заявка, поступившая на вход СМО, либо сразу попадает на обслуживание, если свободен хотя бы один из каналов обслуживания, либо получает отказ и попадает в ту часть выходящего потока, которая соответствует потерям. В каждый момент времени с системой может быть связано не более m заявок, где m - число каналов обслуживания.

Граф переходов m-канальной СМО с отказами приведен на рисунке 3.6.

Рис. 3.6. Размеченный граф состояний системы m-канальной СМО с отказами

Балансы интенсивностей входных и выходных потоков при установившемся режиме работы СМО выглядят следующим образом:

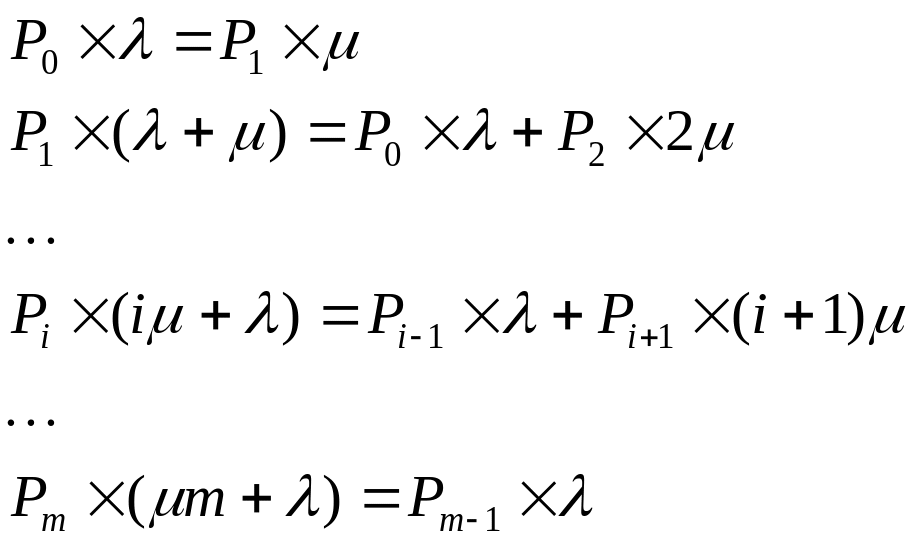
Предельные вероятности состояний системы имеют вид:

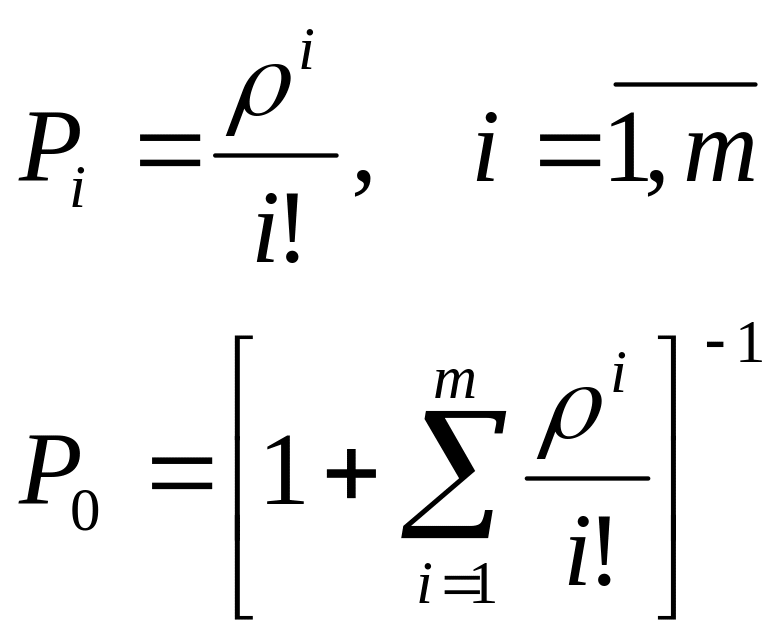
Отказ получает заявка, заставшая СМО в состоянии Sm, следовательно:

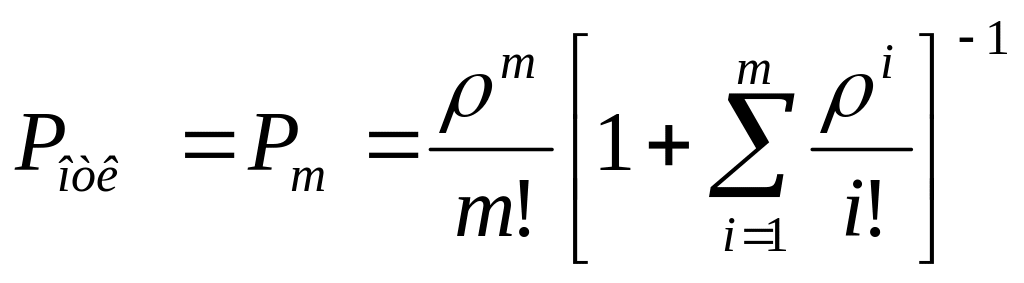
Вероятность обслуживания Р_об и интенсивность потока обслуженных заявок λ⁰ равны, соответственно

Среднее число каналов может быть найдено как отношение интенсивности потока обслуженных заявок λ⁰ к производительности одного канала обслуживания, характеризуемой интенсивностью обслуживания .

Среднее число заявок, связанных с системой, совпадает со средним числом каналов обслуживания