4.7. Точность статистических оценок

Теорема 2. Пусть x₁, x₂, ..., x_n - результаты n независимых измерений СВ , т.е. значения независимых СВ ₁, ..., _n, распределенных по тому же закону, что СВ . Тогда

1) является значением несмещенной статистической оценки математического ожидания СВ , т.е. .

2) - значение несмещенной оценки для D_.

Несмещенность статистической оценки означает, что в среднем оценка равна оцениваемому параметру.

Доверительным интервалом  с доверительной вероятностью  называется такой интервал со случайными границами [^*-; ^*+], где ^* - статистическая оценка параметра, что p{[^*-; ^*+]}, т.е. интервал накрывает истинное значение оцениваемого параметра с вероятностью не меньше .

Функцией Лапласа называется нечетная функция, при неотрицательных t определяемая как , где СВ  распределена по нормальному закону с параметрами m=0 и =1.

Г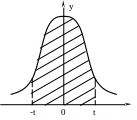 еометрическая интерпретация: Ф(t) - площадь криволинейной трапеции.

Рис. 4.5

Теорема 3. (О радиусе доверительного интервала).

При большом числе наблюдений (n100)

1) В случае =m_

, (3.2)

2) В случае =D_

. (3.3)

Где через t_ обозначено решение уравнения Ф(t)=. Например, t_0,8 = 1,28; t_0,85 = 1,44; t_0,9 = 1,65; t_0,95 = 1,96.

Поскольку, как правило, _ и D_ неизвестны, то вместо них в формулах (1.8), (1.9) используются их оценки и , что не гарантирует доверие, но правдоподобно.

Следствие 1 из теоремы 3. Расчет количества наблюдений, обеспечивающих заданную точность и заданную надежность:

n = (t__/)².

Следствие 2. Для улучшения точности в k раз необходимо увеличить количество наблюдений в k² раз.

4.8. Аппроксимация результатов моделирования

Во многих системах имеет место функциональная связь между двумя или более переменными, и желательно эту связь выявить. Для определения этой связи используется регрессионный анализ, который дает возможность построения уравнения исходя из выборки.

Математическая модель представляется в виде полинома, в который разлагается анализируемая статистическая характеристика системы y = f(x₁, x₂, ..., x_k) по входным параметрам x_i (j=1,k):

где , ,

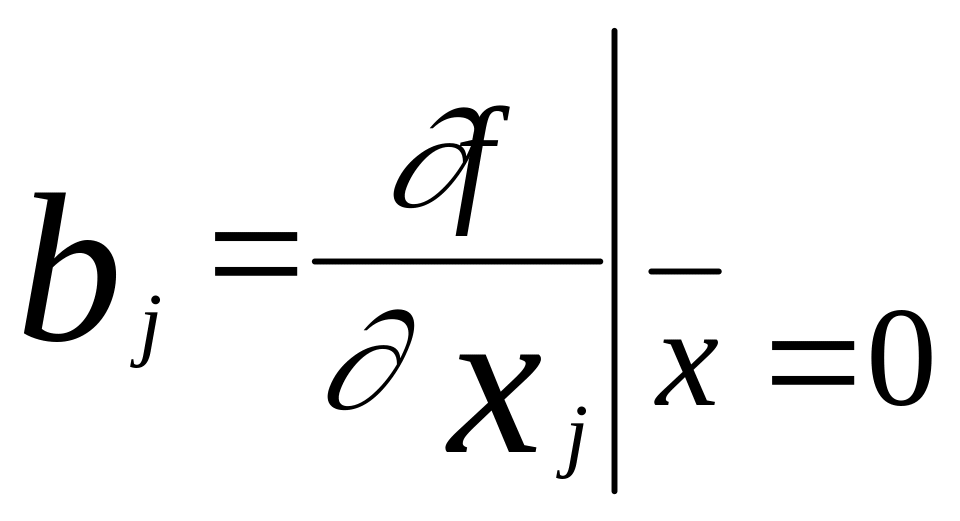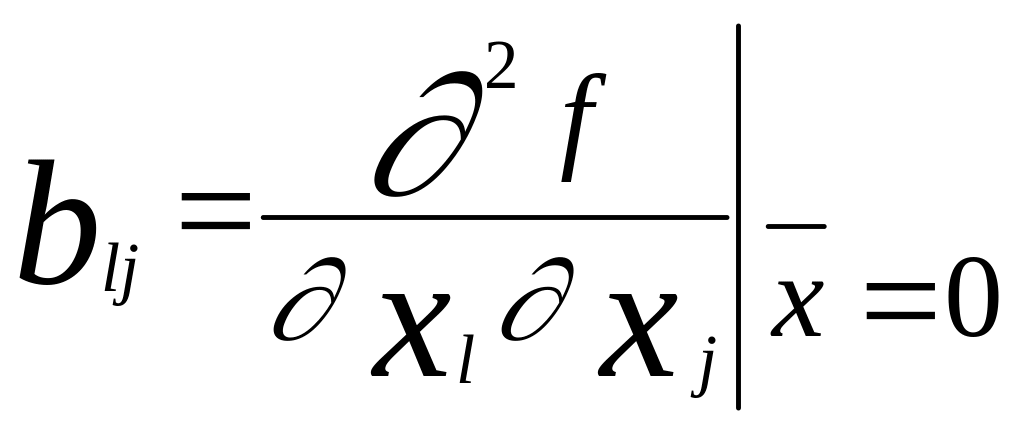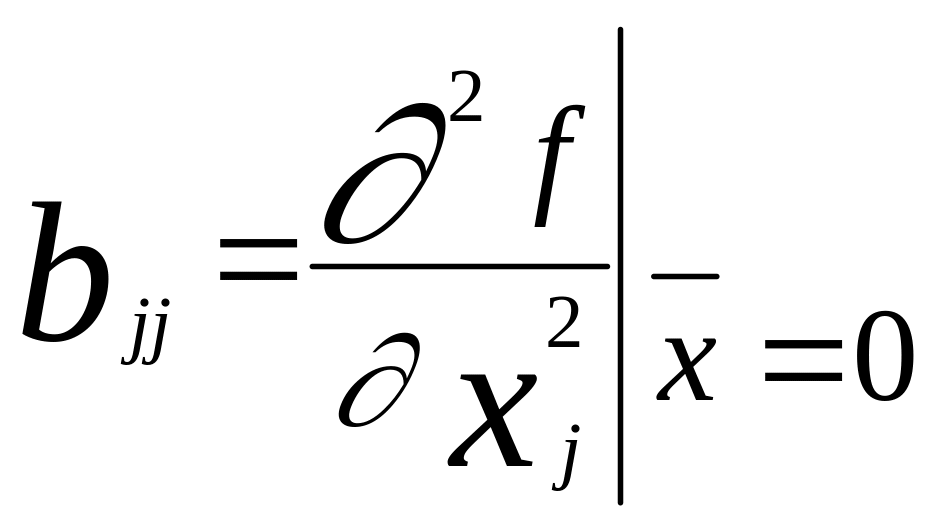
Предположим, что проведена серия из N независимых наблюдений, давших N систем значений y_i, x_1i, x_2i, ..., x_ki (i=1,N) и по этим данным требуется оценить неизвестные коэффициенты b₀, b_j, b_lj, т.е. найти их оценки , . Уравнение регрессии, полученной на основании эксперимента, запишется в следующем виде:

Задача оценки параметров может быть решена применением методов максимального правдоподобия или наименьших квадратов, причем в последнем случае оценки коэффициентов находятся из условия

.

Необходимым условием минимума Ф является выполнение равенств

.

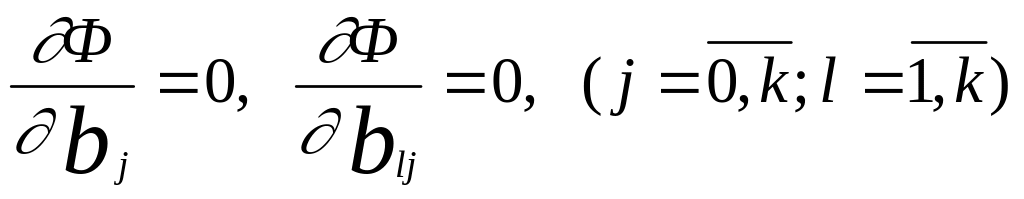Разность между объемом выборки N и числом связей, наложенных на эту выборку p, называется числом степеней свободы выборки f

f=N-p.

При определении уравнения регрессии число связей p равно числу определяемых коэффициентов, а вид уравнения регрессии выбирается путем экспериментального подбора.

После того, как уравнение регрессии найдено, прежде чем принять какое либо решение по поводу модели, необходимо проверить гипотезу о том, что полученная модель удовлетворительно описывает экспериментальные данные. Для этого необходимо проверить значимость всех коэффициентов регрессии и адекватность модели.

При проверке значимости коэффициентов регрессии для каждого коэффициента b_j выдвигают гипотезу H0:(b_j=0). Известно, что оценка имеет нормальное распределение со средним, равным истинной величине b_j и дисперсией

,

а величина

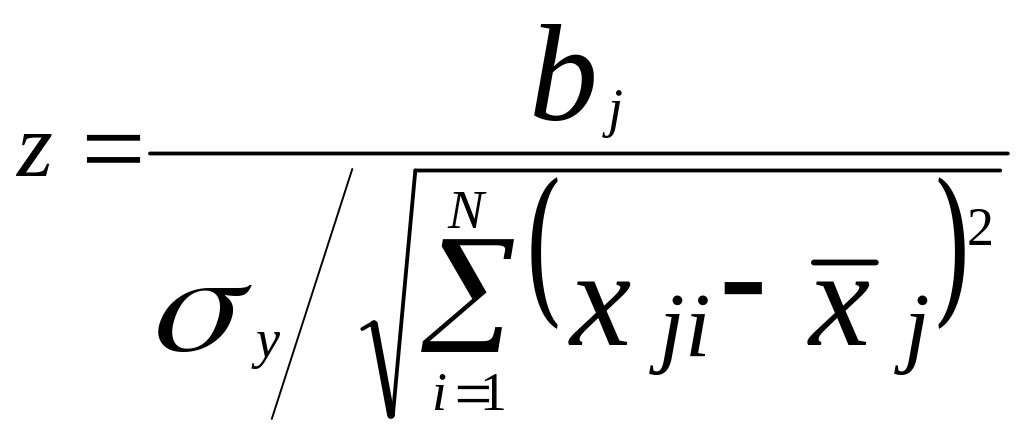
имеет стандартное гаусовское распределение. Величину z можно использовать для проверки гипотезы H₀. Если неизвестна, то используя вместо нее оценку , получим

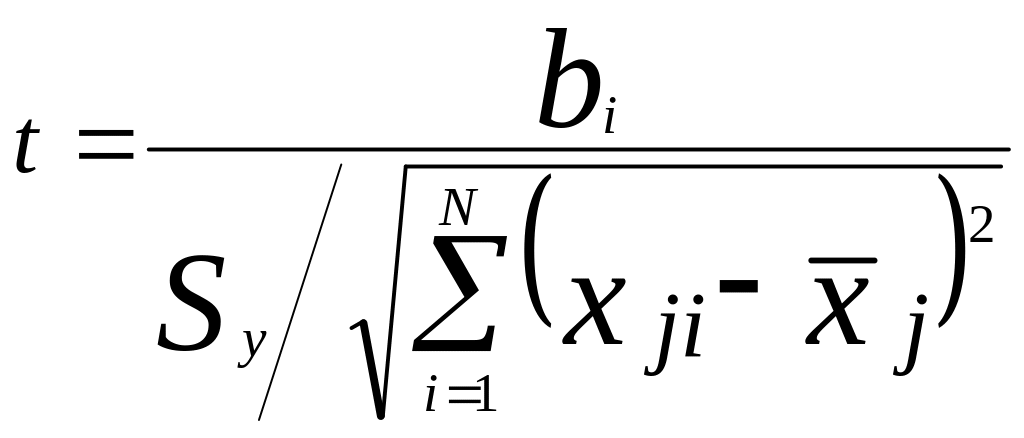
Величина t распределена как стьюдентовская величина с N-2 степенями свободы. Поэтому, если для заданного уровня значимости  получено , гипотеза H₀ должна быть отвергнута, т.е. коэффициент b_j значимо отличается от нуля.

В модели множественной регрессии незначимые коэффициенты исключаются из уравнения. Оставшиеся коэффициенты пересчитываются, поскольку в общем случае они коррелированны друг с другом.

Проверка адекватности полученной модели производится по критерию Фишера:

,

где ,

.

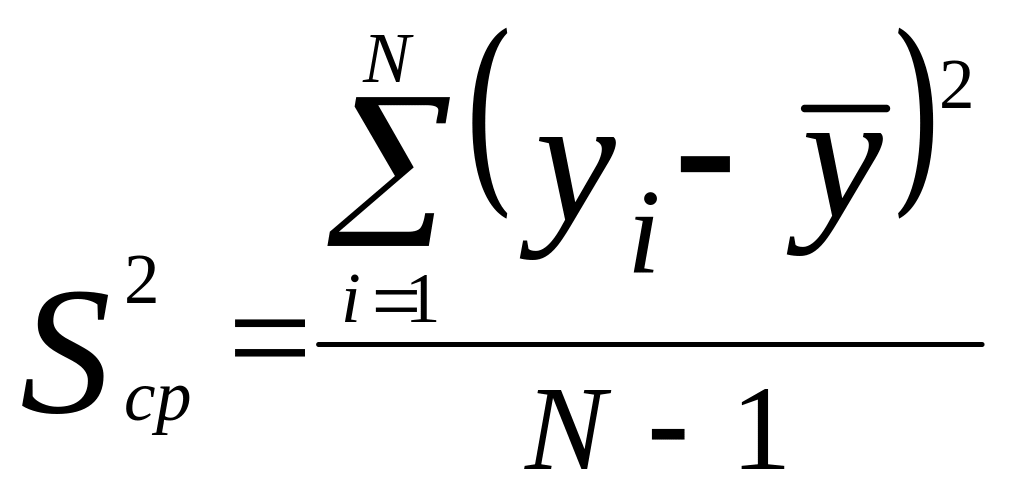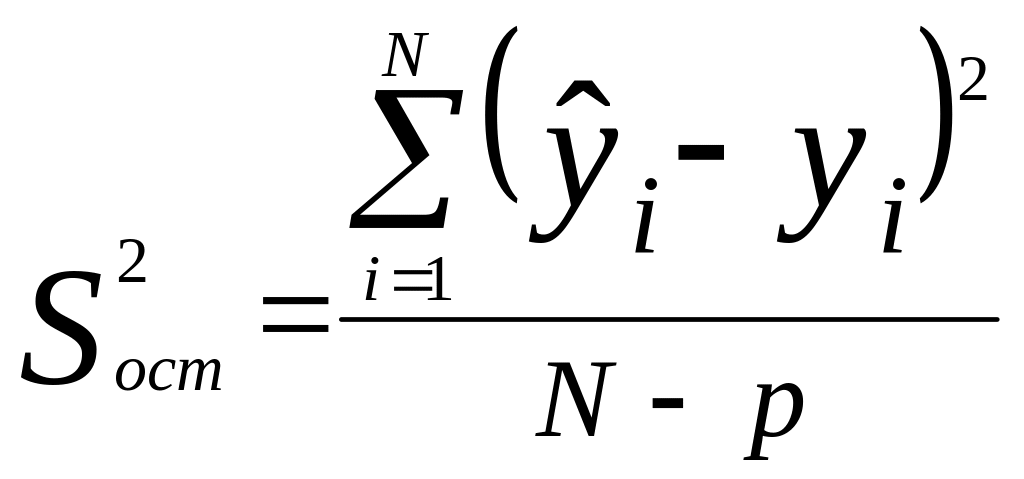Критерий Фишера показывает, во сколько раз уменьшится рассеяние относительно полученного уравнения регрессии по сравнению с рассеянием относительно генерального среднего. Чем больше значение F превышает табличное F_(f₁,f₂) для выбранного уровня значимости  и чисел степеней свободы f₁=(N-1) и f₂=N-p, тем эффективнее уравнение регрессии.