
- •Воронежский государственный технический университет
- •Утверждено Редакционно-издательским советом университета в качестве учебного пособия
- •Введение
- •2. Классификация видов моделирования систем
- •3. Основные математические методы моделирования информационных процессов и систем
- •3.1. Виды математических моделей
- •3.2. Структурные математические модели
- •3.3. Функциональные математические модели
- •3.3.1. Непрерывно-детерминированные модели
- •3.3.2. Непрерывно-стохастические модели
- •3.3.2.1. Анализ работы разомкнутых смо
- •3.3.2.2. Замкнутые смо
- •3.4. Моделирование дискретных систем
- •3.4.1. Конечные автоматы
- •3.4.2. Дискретно-детерминированные модели
- •3.4.3. Вероятностные автоматы
- •3.5. Сетевые модели. Сети Петри (n-схемы)
- •4. Имитационное моделирование информационных процессов
- •4.1. Организация статистического моделирования
- •4.2Моделирование случайной величины с заданным законом распределения
- •4.3 Моделирование равномерно распределенных на отрезке [a,b] случайных чисел
- •4.4. Моделирование показательно распределенных св
- •4.5. Моделирование нормально распределенных случайных чисел
- •4.6. Проверка качества случайных чисел по критерию
- •4.7. Точность статистических оценок
- •4.8. Аппроксимация результатов моделирования
- •5. Формализация и алгоритмизация процессов функционирования систем
- •5.1. Методика разработки и машинной реализации моделей систем
- •5.2. Построение концептуальных моделей систем и их формализация
- •5.3. Алгоритмизация моделей систем и их машинная реализация
- •6. Планирование имитационных моделй с экспериментами
- •6.1. Полный факторный эксперимент
- •6.2. Дробные реплики
- •6.3. Общая схема планирования эксперимента
- •6.3.1. "Крутое восхождение"
- •6.3.2. Этапы планирования эксперимента
- •6.4. Стратегическое планирование
- •6.5. Тактическое планирование
- •7. Оценка точности и достоверности результатов моделирования
- •7.1. Общие положения
- •7.2. Регрессионный анализ
- •7.3. Корреляционный анализ
- •7.4. Экспертные оценки
- •8. Инструментальные средства моделирования систем
- •8.1. Архитектура языков имитационного моделирования
- •8.2. Задание времени в машинной модели
- •8.3. Сравнительный анализ языков моделирования
- •8.4. Примеры прикладных пакетов моделирования и языков моделирования
- •9. Правила построения моделирующих алгоритмов и способы реализации моделей
- •10. Сетевые модели вычислительных систем
- •10.1. Определение: Сеть Петри
- •Объекты, образующие сеть Петри
- •2Расширенная входная Расширенная выходная
- •10.2. Маркировка сети Петри.
- •10.3. Пространство состояний сети Петри
- •10.4. Моделирование параллельных процессов.
- •10.5. Моделирование процессора с конвейерной обработкой
- •10.6. Кратные функциональные блоки компьютера
- •10.7. Сети Петри и программирование
- •10.8. Взаимно исключающие параллельные процессы
- •10.9. Анализ сетей Петри
- •10.10. Дерево достижимости сети Петри
- •В позицию может входить и выходить только одна дуга
- •11. Система имитационного моделирования gpss/pc
- •11.1. Назначение и основные возможности системы
- •11. 2. Состав системы моделирования gpss/pc
- •11.3. Структура операторов языка gpss/pc
- •11.4. Команды среды gpss/pc
- •11.5. Основные операторы языка gpss/pc
- •11.5.1. Начало gpss-модели
- •11.5.2. Комментарии в gpss/pc
- •11.5.3. Имитация потоков событий. Транзакты
- •11.5.4. Имитация типовых узлов смо
- •11.6. Информация о ходе моделирования
- •11.6.1. Окно данных
- •11.6.2. Окно блоков
- •11.6.3. Окно устройств
- •11.6.4. Окно многоканальных устройств
- •11.7. Информация о результатах моделирования
- •11.7.1. Файл результатов моделирования
- •11.7.2. Содержание результатов моделирования
- •11.9. Управление движением транзактов
- •11.10. Дополнительные средства сбора информации о модели
- •11.11. Стандартные числовые атрибуты
- •11.12. Выбор направления движения транзактов с использованием сча
- •11.13. Датчики случайных чисел в gpss/pc
- •11.14. Функции в gpss/pc
- •11.14.1. Дискретные функции
- •11.14.2. Непрерывные функции
- •11.15. Переменные в gpss/pc
- •11.16. Организация циклов
- •11.17. Логические переключатели
- •11.18. Управление движением транзактов в зависимости от состояния элементов модели
- •11.19. Моделирование согласованных процессов на gpss-pc
- •11.19.1. Создание ансамблей транзактов
- •11.19.2. Накопление нескольких транзактов для последующей обработки
- •11.19.3. Объединение нескольких транзактов в один
- •11.19.4. Синхронизация движения транзактов в модели
- •11.20. Время пребывания транзакта в модели
- •11.21. Сбор данных о распределении значений характеристик модели. Таблицы
- •11.22. Изменение имени файла результатов моделирования
- •11.23. Приведение модели к исходному состоянию
- •11.24. Многократное выполнение моделирования
- •11.25. Моделирование нескольких вариантов системы в одной gpss-модели
- •11.26. Время моделирования
- •3 94026 Воронеж, Московский просп., 14
3. Основные математические методы моделирования информационных процессов и систем
3.1. Виды математических моделей
Условимся делить математические модели на два класса: структурные и функциональные, которые, в свою очередь, будем подразделять на непрерывные (позволяют отразить непрерывные процессы) и дискретные (служат для описания дискретных процессов). Те и другие модели могут быть детерминированными (отображают процессы, в которых предполагается отсутствие всяких случайных воздействий) и стохастическими (отображают вероятностные процессы и события). Кроме того, математическое моделирование может отображать как функциональное взаимодействие элементов системы, так и развитие процессов её функционирования, и в этом смысле удобно рассматривать аналитическое, имитационное и комбинированное моделирование.
Для аналитического моделирования характерно, что процессы функционирования системы записываются в виде некоторых функциональных соотношений (алгебраических, интегро-дифференциальных, конечно-разностных) или логических условий. Методы исследования аналитической модели: а) аналитические; б) численные; в) качественные.
При имитационном моделировании реализующий модель алгоритм воспроизводит процесс функционирования системы S во времени, имитируются элементарные явления, составляющие процесс, с сохранением их логической структуры и последовательности протекания во времени.
Комбинированное (аналитико-имитационное) моделирование при анализе и синтезе систем позволяет объединить достоинства аналитического и имитационного моделирования. При построении комбинированных моделей проводится предварительная разбивка процесса функционирования объекта на подпроцессы и для тех из них, где это возможно используются аналитические модели, а для остальных строятся имитационные модели.
3.2. Структурные математические модели
Структурные математические модели предназначены для отображения структурных свойств объекта. Различают структурные модели топологические и геометрические.
Топологические отображают состав и взаимосвязи элементов объекта и применяются для описания сложных объектов, состоящих из большого числа элементов. Такие модели могут иметь форму графа или соответствующих им матриц. (Примеры: компоновка оборудования, размещение деталей, трассировка соединений, разработка расписаний).
Геометрические отображают совокупность данных, определяющих геометрическую форму объекта. Различают алгебрологические, аналитические, канонические, рецепторные, каркасные, кинематические и геометрические макромодели.
3.3. Функциональные математические модели
Математическая модель М объекта моделирования S можно представить в виде множества величин, описывающих процесс функционирования этого объекта и образующих в общем случае следующие подмножества: (рис. 3.1)
совокупность входных воздействий на систему xiX,
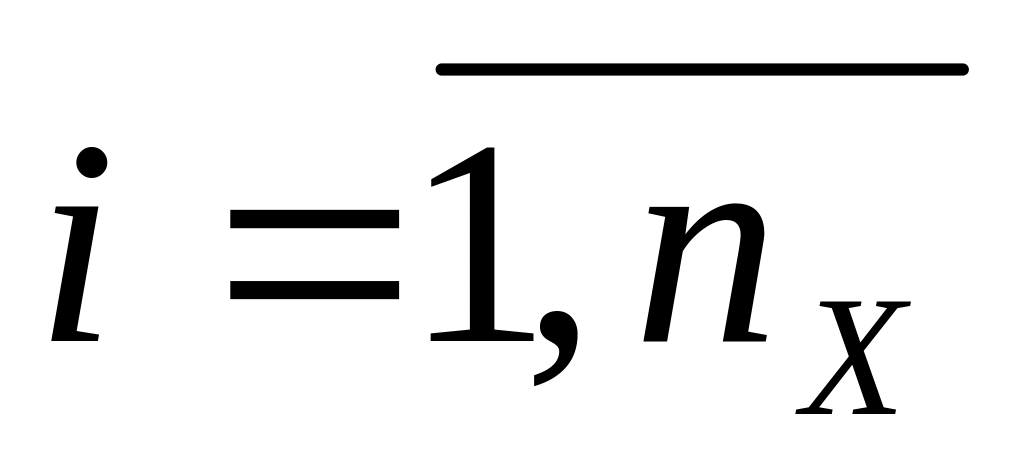 ;
;совокупность воздействий внешней среды vjV,
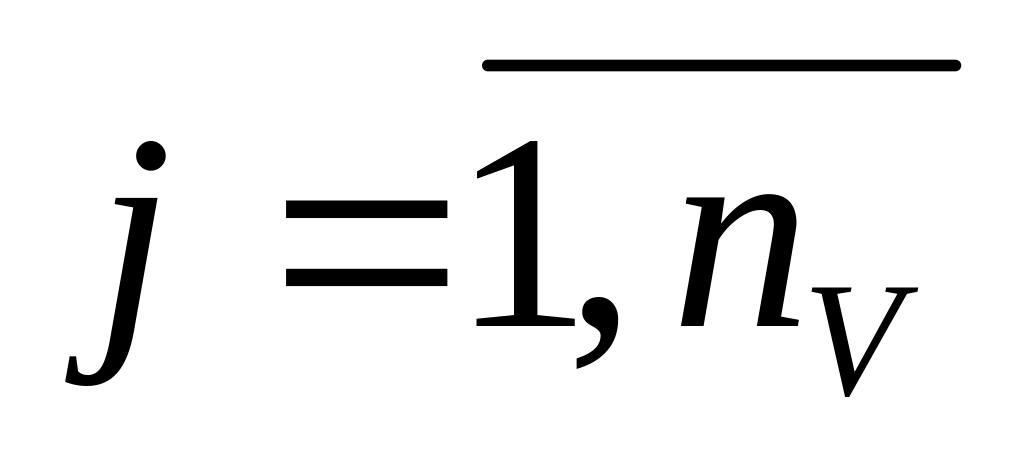 ;
;совокупность внутренних параметров системы hkH,
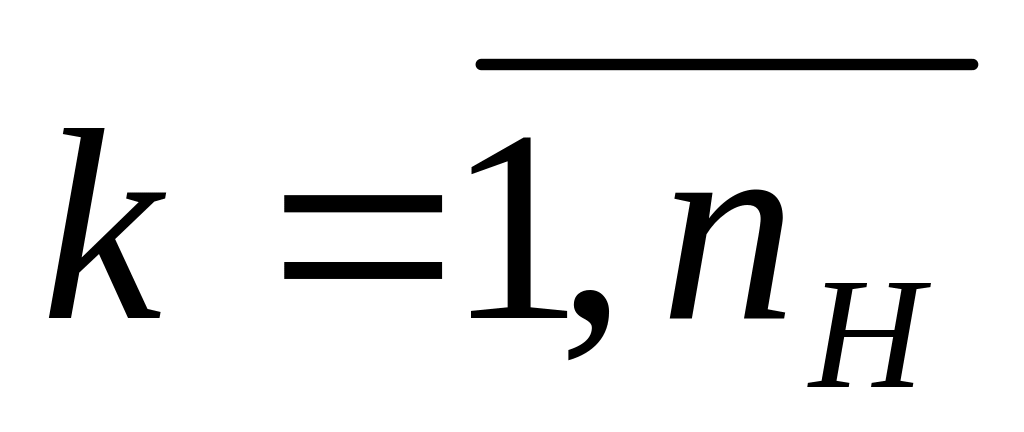 ;
;совокупность выходных характеристик системы ylY,
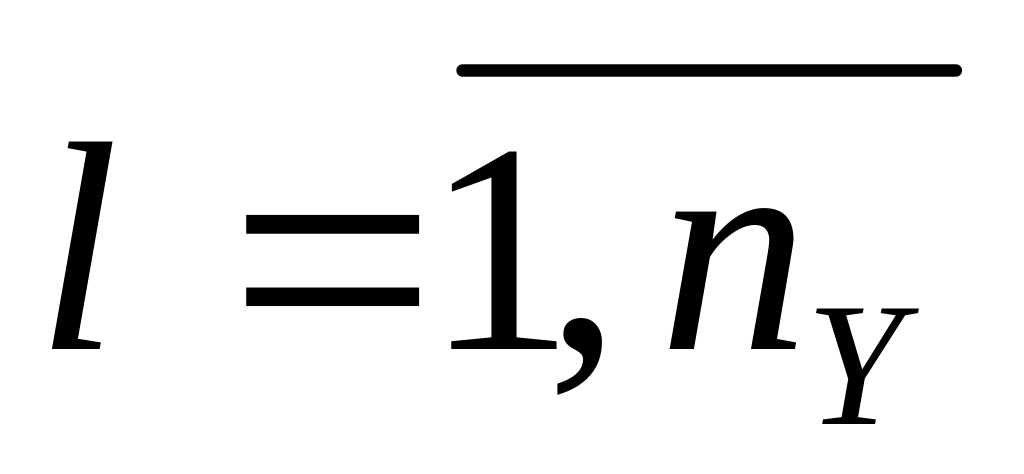 .
.
П ри
этом входные воздействия, воздействия
внешней среды и внутренние параметры
являются независимыми переменными
(экзогенными), а выходные – зависимыми
(эндогенными) переменными. Среди
этих переменных могут быть управляемые
ри
этом входные воздействия, воздействия
внешней среды и внутренние параметры
являются независимыми переменными
(экзогенными), а выходные – зависимыми
(эндогенными) переменными. Среди
этих переменных могут быть управляемые

Рис. 3.1 Схема математической модели
и неуправляемые. Иногда, управляемые называют параметрами.
Математическое описание поведения объекта моделирования во времени t можно представить в следующем виде:
![]() ,
,
где F – оператор, преобразующий экзогенные переменные в эндогенные в соответствии с приведенным соотношением,
а для статических моделей в форме равенства:
![]() ,
,
то есть отображение между двумя подмножествами свойств моделируемого объекта Y и {X, V, H}.
Эти зависимости называются законами функционирования системы.
При построении математических функциональных моделей можно выделить следующие основные подходы: непрерывно-детерминированный (аналитические модели), непрерывно-стохастический (статистические модели и системы массового обслуживания), дискретно-детерминированный (конечные автоматы), дискретно-стохастический (вероятностные автоматы) обобщённый или универсальный (агрегативные системы). Соответственно этим подходам были разработаны типовые математические схемы создания моделей.
