4.2Моделирование случайной величины с заданным законом распределения

Большинство случайных величин можно смоделировать при помощи равномерно распределенной на отрезке [0,1] случайной величины.

Теорема 1.

Пусть СВ  равномерно распределена на отрезке [0,1], G(x) - заданная функция распределения. Тогда СВ =G^-1() имеет совпадающую с G(x) функцию распределения F_(x)=G(x) (рис. 4.1).

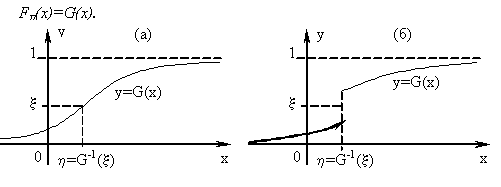
Рис. 4.1. Графическое представление теоремы 1.

Если функция G «проскакивает» значение , то полагаем =G^-1() равным точке разрыва.

4.3 Моделирование равномерно распределенных на отрезке [a,b] случайных чисел

Статистические характеристики случайной величины , равномерно распределенной на интервале [a,b]:

плотность распределения имеет вид:

Вероятность попадания значений СВ  в любую область длины  из отрезка [a,b] равна /(b-a) и, следовательно, не зависит от размещения этой области в пределах отрезка [a,b].

Функция распределения СВ

Мат. ожидание: .

Дисперсия: .

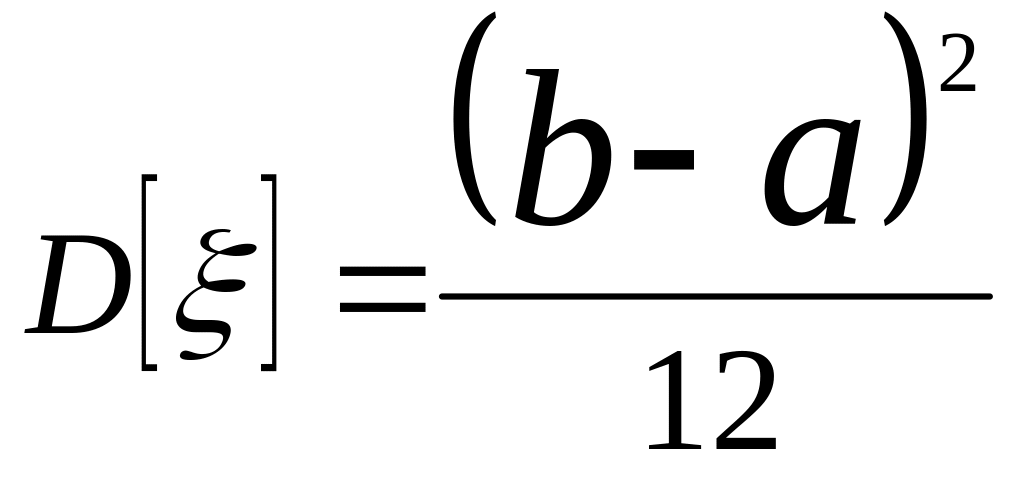Графическое решение задачи, согласно теореме 1 показано на рисунке4.2.

Рис. 4.2. Функция распределения для равномерно распределенной СВ.

Из уравнения находим .

4.4. Моделирование показательно распределенных св

СВ  называется показательно распределенной с параметром >0 , если ее плотность имеет вид

где >0 некоторое число.

Известно, что

Из уравнения (рис. 4.3) =1-е^-

н аходим

По теореме 1 функция распределения СВ  совпадает с F_(х). Заметим, что СВ 1-, так же как и СВ , равномерно распределена на отрезке [1,0]. Поэтому можно для моделирования использовать формулу требующую на одно арифметическое действие меньше.

4.5. Моделирование нормально распределенных случайных чисел

СВ  распределена по нормальному закону с параметрами m и  (>0), если ее плотность имеет вид

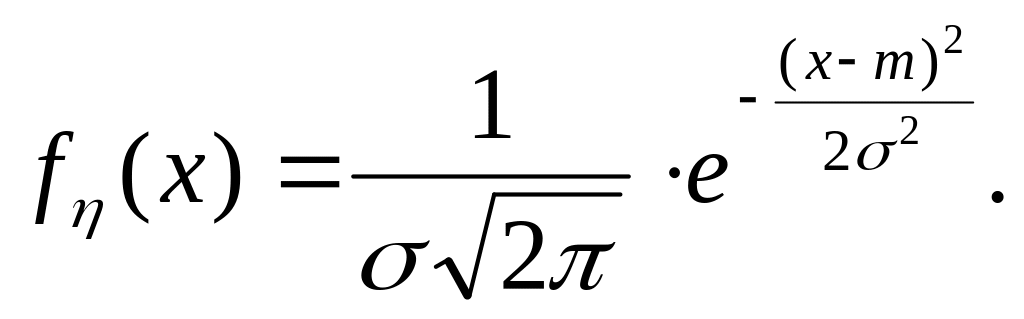
Известно, что М[]=m, D[]=².

П оскольку интеграл

в данном случае не выражается через элементарные функции, теорема 1 не позволяет получить экономный метод моделирования нормально распределенных чисел.

Пусть ₀=₁+₂+…+₁₂ – 6, где СВ _i – независимы и равномерно распределены на отрезке [0,1]. С учетом того, что для всех i получим

По центральной предельной теореме теории вероятностей СВ ₀ распределена по близкому к нормальному закону. То же верно и для СВ =₀+m, причем М[]=m, D[]=².

4.6. Проверка качества случайных чисел по критерию

Для проверки соответствия опытных данных заданному закону распределения можно оценить близость частот, с которыми данные попадают в некоторые интервалы, к вероятностям попадания в эти интервалы значений случайной величины, вычисленным в соответствии с заданным законом распределения.

Численной мерой близости теоретической (f) и статистической (f^*) плотности распределения служит величина

,

где N - количество наблюдений;

I - число интервалов разбиения;

n_i - количество наблюдений, попавших в i-й интервал;

p_i - вероятность попадания СВ в i-й интервал в соответствии с заданным законом распределения.

Если гипотеза о заданном законе распределения справедлива, то число является одним из значений случайной величины, распределенной по закону, близкому к распределению с k=I-s степенями свободы (s - число оцениваемых по опытным данным параметров закона распределения). Для заданного уровня значимости  по статистическим таблицам выбирается критическое значение , из условия , т.е. событие маловероятно в случае справедливости гипотезы о законе распределения. При считаем, что данные не противоречат сделанному предположению.