Tipovye_raschyoty_pri_sooruzhenii_i_remonte
.pdf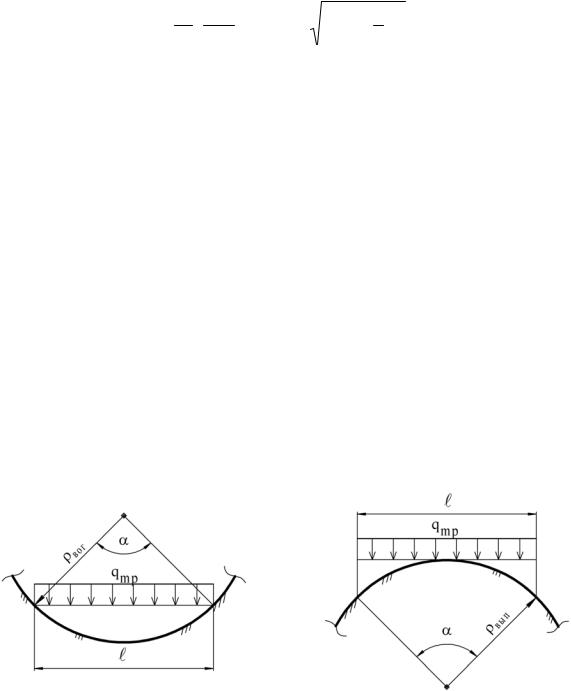
Получаемое несоответствие между изогнутой осью трубопровода и осью траншеи должно удовлетворять условию вписываемости трубы в траншею. Как показывают расчеты, наибольшее расхождение осей трубопровода и траншеи
достигается в точке x = 23 l:
∆у |
|
= у |
|
− y = |
14 |
|
Pl3 |
|
ρ |
|
− |
ρ |
2 |
− |
4 |
l |
2 |
|
, |
(2.159) |
max |
тр |
|
|
− |
гор |
гор |
|
|
|
|||||||||||
|
|
|
81 |
|
ΕI |
|
|
|
|
|
9 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
и не должно превышать допустимого значения |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
∆уmax ≤ [∆у]= (B − Dн.и )/ 2 |
, |
|
|
|
|
|
(2.160) |
|||||||||
где В – ширина траншеи по дну; Dн.и – диаметр заизолированного трубопровода; P – усилие, необходимое для изгиба трубопровода, определяемое по формуле (2.157).
Если трубопровод не вписывается в траншею, т.е. не выполняется условие (2.160), следует увеличить ширину траншеи по дну В или уменьшить
длину изгибаемого участка l, осуществляя требуемый поворот изгибом нескольких участков меньшей длины.
2.6.2. Вертикальный поворот
Различают вертикальный поворот на вогнутом рельефе местности (рис. 2.23) и вертикальный поворот на выпуклом рельефе местности
(рис.2.24).
Рис.2.23. Расчетная схема вертикального поворота на вогнутом рельефе
Рис.2.24. Расчетная схема вертикального поворота на выпуклом рельефе
129
Радиусы поворотов трубопровода в вертикальной плоскости определяются из двух условий: условия прочности и условия прилегания трубопровода ко дну траншеи под действием собственного веса. Поскольку ось трубопровода, изогнутого под действием собственного веса, представляет параболу, а профи дна траншеи – дугу окружности, зависимости, предложенные ниже, составлены с учетом того, что в точке наибольшей кривизны трубопровода радиус упругого изгиба был больше или равен величине, определяемой по табл.2.10.
На вогнутом рельефе местности радиус ρвог из условия прочности определяется по формуле:
ρвог ≥ 3ΕDн 5σи , |
(2.161) |
из условия прилегания ко дну траншеи – по формуле:
|
|
|
384ΕI |
|
|
− cos |
α |
|
|
|
|
|
1 |
2 |
|
|
|||
ρ |
вог |
= 3 |
|
|
|
α4 |
, |
(2.162) |
|
|
|
5q |
|
|
|
|
|||
|
|
|
|
|
тр |
|
|
|
|
где α - угол поворота трассы в радианах; qтр – расчетная нагрузка от собственного веса трубопровода, qтр=qм + qиз.
На выпуклом рельефе местности радиус ρвып из условия прочности
ρвып ≥ ΕDн / 2σи , |
(2.163) |
из условия прилегания ко дну траншеи – по формуле: |
|
8ΕI |
|
ρвып = 3 q α2 . |
(2.164) |
тр |
|
130
2.7. Примеры расчетов
Пример 2.1. Определить толщину стенки трубы для участка газопровода Оренбург-Уфа при следующих исходных данных: Dн= 1020 мм;
р =7,4 МПа; tэ=+19 °С; тип прокладки – подземная.
Решение
1. По табл. 1.1 участок газопровода относится к IV категории, по табл. 1.2 для IV категории m=0,90. По сортаменту (см.приложение Г) для газопровода выбираем трубы, выпускаемые Выксунским металлургическим заводом из
стали марки 10Г2ФБЮ с σв = R1н = 589 МПа и σт = R2н =461 МПа, k1=1,34, kн=1
(табл.2.6).
2. Расчетное сопротивление металла труб по формуле (2.34)
R = |
589 0,9 |
= 395,6 МПа. |
|
|
|||
1 |
1,34 |
1 |
|
|
|
||
3. Толщина стенки газопровода по формуле (2.36) с коэффициентом надежности по нагрузке от внутреннего давления np=1,1
δ = |
|
1,1 7,4 1,02 |
= 0,01028 м. |
|
|
|
||
2(395,6 +1,1 7,4) |
|
|
|
|||||
|
|
|
|
|
|
|||
4. Полученное расчетное значение толщины стенки округляем до |
||||||||
ближайшего большего |
|
по |
сортаменту, |
равного |
δн= |
0,0103 |
м, |
|
Dвн=1020-2·10,3=999,4 мм. По СНиП 2.01.07-85*, [112] находим для района |
||||||||
прокладки трубопровода tI |
= |
-15 °C; tVIII= +20 |
°С; ∆I = |
20°С; |
∆VII = 6 |
°С. |
||
Нормативные значения температуры наружного воздуха в холодное и теплое
время года: tнx = -15 -20 = 35 °С, tнm = +20 +6 + 26 °С, а расчетные значения tx = -35 -6 + -41 °C; tm = +26 +3 = +29 °C.
Температурный перепад при замыкании трубопровода в холодное время года ∆t x =+19 – (-41) = +60 °С, а при замыкании в теплое время года
∆tm = +19 – (+29) = -10 °С.
В качестве расчетного температурного перепада принимаем наибольшее значение ∆t =+60 °С.
5. Продольные напряжения по формуле (2.40)
σпрN = -1,2·10-5·2,1·105·60+0,3·1,1 7,4 0,9994 = -32,7 МПа. 2 0,0103
131
6. Знак «минус» указывает на наличие осевых сжимающих напряжений, поэтому необходимо определить по формуле (2.39) коэффициент Ψ1 ,
учитывающий двухосное напряженное состояние металла труб:
Ψ1 |
= |
|
|
− 32,7 |
2 |
− 32,7 |
= 0,956 . |
1 − 0,75 |
|
− 0,5 |
395,6 |
||||
|
|
|
|
395,6 |
|
|
|
7. По формуле (2.38) пересчитываем значение толщины стенки |
|||||||
газопровода |
|
|
|
|
|
|
|
|
δ = |
1,1 7,4 1,02 |
= 0,0107м . |
||||
|
2(0,956 395,6 +1,1 7,4) |
||||||
8. Большее ближайшее значение толщины стенки по сортаменту равно 10,8 мм. Если мы примем эту толщину стенки трубы, то значение продольных осевых напряжений:
σпр.N = −1,2 10−5 2,1 105 60 + 0,3 |
1,1 7,4 0,9984 |
= −38,2 |
МПа . |
|
2 0,0108 |
||||
|
|
|
Тогда
Ψ1 = |
− 38,2 |
2 |
− 0,5 |
38,2 |
= 0,947 |
; |
|
1 − 0,75 |
|
395,6 |
|||||
|
|
395,6 |
|
|
|
|
|
δ = |
|
1,1 7,4 1,02 |
|
= 0,0108 м = 10,8 мм . |
|||
2(0,947 395,6 +1,1 7,4) |
|||||||
Принятая толщина стенки удовлетворяет условиям.
Dн / 140 =1,02 / 140 + 0,0073<0,0108,
0,004<0,0108.
Очевидно, что δн=10,8 мм можно принять за окончательный результат.
Пример 2.2. Проверить на прочность и по деформациям трубопровод, рассчитанный в предыдущем примере.
Исходные данные: Dн= 1020 мм; Dвн=998,4 мм; δн10,8 мм; R1=395,6 МПа; R2н =461 МПа; p=7,4 МПа; ∆t x =60 °С; ∆tТ =-10 °С; σпрN =-38,2 МПа;
m = 0,9; ρmin = 1000 м.
132
Решение
1. Значение кольцевых напряжений σкц по формуле (2.9)
σкц = |
1,1 7,4 0,9984 |
= 376 |
МПа. |
|
2 0,0108 |
||||
|
|
|
2.Коэффициент, учитывающий двухосное напряженное состояние металла трубы Ψ2 по формуле (2.45)
Ψ2 =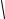 
1 − 0,75 395376,6 2 − 0,5 395376,6 = 0,093.
3.Проверяем прочность трубопровода в продольном направлении по условию (2.44)
−38,2 ≤ 0,093 395,6
38,2>36,8 МПа, т.е. условие не выполняется.
Увеличиваем толщину стенки трубы до ближайшего большего значения по сортаменту (приложение Г), приняв δн=12,3 мм =0,0123 м, при этом
внутренний диаметр трубы будет равен
Dвн =1020 − 2 12,3 = 995,4 мм.
4. |
Напряжения σкц по формуле (2.9) |
|
|
|
|
||||
|
σкц = |
1,1 7,4 0,9954 |
|
= 329,4 МПа. |
|
||||
|
2 0,0123 |
|
|||||||
|
|
|
|
|
|
||||
5. |
Коэффициент Ψ2 по формуле (2.45) |
|
|
|
|||||
|
|
|
329,4 |
2 |
|
|
329,4 |
= 0,2765. |
|
|
Ψ2 = 1 − 0,75 |
|
− 0,5 |
395,6 |
|||||
|
|
|
395,6 |
|
|
|
|
|
|
6. |
Продольные напряжения σпрN по формуле (2.40) |
|
|||||||
|
σпрN = −1,2 10−5 2,1 105 60 + 0,3 |
1,1 7,4 0,9954 |
= −52,4 МПа. |
||||||
|
2 0,0123 |
||||||||
|
|
|
|
|
|
|
|||
7.Проверяем условие (2.44)
−52,4 ≤ 0,2765 395,5
133
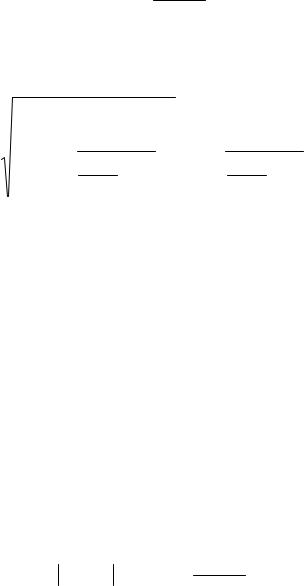
52,4<109,4 МПа, т.е. условие выполняется.
8.Для проверки по деформациям находим сначала кольцевые напряжения
σкцн от действия нормативной нагрузки – внутреннего давления по формуле
(2.51)
σкцн = |
7,4 0,9954 |
= 299,4 МПа. |
|
2 0,0123 |
|||
|
|
9. Проверяем условие (2.47)
299,4 ≤ 0,90,91,0 461 299,4<461 МПа, т.е. условие выполняется.
10. Коэффициент Ψ3 по формуле (2.50)
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
299,4 |
|
|
|
299,4 |
|
||||
Ψ3 = |
|
|
− 0,5 |
|
= 0,5027 . |
||||||
1− 0,75 |
0,9 |
|
|
|
0,9 |
|
|
||||
|
|
|
461 |
|
|
|
461 |
|
|||
|
|
0,9 |
1 |
|
|
|
0,9 |
1 |
|
||
|
|
|
|
|
|
|
|
||||
11. Определяем значение продольных напряжений σпрн |
по формуле (2.48) |
• для положительного температурного перепада |
|
σпрн = 0,3 299,4 −1,2 10−5 2,1 105 60 − 2,1 105 1,02 = |
-168,5 МПа. |
|
2 1000 |
|
|
• для отрицательного температурного перепада |
|||
σпрн = 0,3 299,4 +1,2 10−5 2,1 105 10 + |
2,1 105 1,02 |
= 221,1 МПа. |
|
2 1000 |
|||
|
|
||
12.Выполнение условия (2.46) проверяем дважды:
•для положительного температурного перепада
−168,5 ≤ 0,5027 0,90,91,0 461 168,5<231,7 МПа, т.е. условие выполняется;
134
• для отрицательного температурного перепада
222,1 ≤0,5027 0,90,91,0 461
222,1<231,7 МПа, т.е. условие выполняется.
Таким образом, окончательно с учетом всех проверок принимаем трубу
Dн ×δ =1020×12,3 мм.
Пример 2.3. Проверить общую устойчивость в продольном направлении прямолинейных и упругоизогнутых участков подземного газопровода 1У категории.
Исходные данные: Dн = 1,02 м; Dвн = 0,9954 м; δн= 12,3 мм; p= 7,4 МПа; ∆t = 60 °С; σкц + 329,4 МПа; ρ =1000 м; hо = 1,0м; грунт – песок; γгр= 16 кН/м3;
ϕгр = 36°; сгр=0; kо = 2 МН/м3; γ м =78,5 кН/м3; изоляционное покрытие «Поликен 980-25», однослойное, ρи.п = 1046 кг/м3; δи.п = 0,635 мм; обертка «Поликен
955-25», однослойная, ρоб = 1028 кг/м3;δоб =0,635 мм; kиз = 1,09; nс.в=0,95.
Решение
1. Площадь поперечного сечения металла трубы
F= π4 (1,022 −0,99542 )= 0,039 м2.
2.Эквивалентное продольное усилие по формуле (2.61)
S= (0,2 329,4 +1,2 10−5 2,1 105 60) 0,039 = 8,466 МН.
3.Осевой момент инерции поперечного сечения трубы
I= 64π (1,024 − 0,99544 )= 4,94 10−3 м4.
4.Нагрузка от собственного веса трубопровода:
•нормативная qмн = 78500 0,039 = 3061,5 Hм ;
•расчетная qм = 0,95 3061,5 = 2908,4 Нм .
135
5. Нагрузка от веса изоляционного покрытия:
• нормативная
qизн =1.09 π 1,02 0,635 10−3 1046 9,8 +1.09 π 1,02 0,635 10−3 × ×1028 9,8 = 45 Нм ;
•расчетная qиз = 0,95 45 = 43 Нм .
6.Нагрузка от веса, транспортируемого продукта:
•нормативная по (2.13) qпрн =10−2 7,4 1,022 = 770 Нм ;
•расчетная qпр = 0,95 770 = 731,4 Нм .
7.Нагрузка от собственного веса заизолированного трубопровода с перекачиваемым продуктом по формуле (2.66)
|
qтр = 2908,4 + 43 + 731,4 = 3683 |
Н. |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
м |
|
|
|
|
|
|
|
|
8. Среднее удельное давление на трубопровод по формуле (2.65) |
||||||||||||||||
|
|
|
1,02 |
|
|
|
1,02 |
2 |
|
o |
|
36 |
o |
|
|
||
|
|
+ |
+ |
1,0 + |
45 |
− |
|
|
+ 3683 |
||||||||
|
2 0,8 16000 1,02 1,0 |
|
|
tg |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||
|
|
|
8 |
|
|
|
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pгр = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
||
|
|
|
π |
1,02 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
=13531,5 Па.
9.Предельные касательные напряжения по формуле (2.64)
τпр =13531,5 tg36o + 0 = 9831Па = 9,831 10−3 МПа.
10.Сопротивление грунта продольным перемещениям трубопровода по формуле (2.63)
pо =π 1,02 9,831 10−3 = 31,5 10−3 МН/м.
11. Сопротивление вертикальным перемещениям по формуле (2.67)
qв = 0,8 16000 1,02 (1,0 + 1,02 − π 1,02) + 3683 =18175Н/м =18,175 10−3 МН/м. 2 8
136
12. Критическое усилие для прямолинейного участка трубопровода в случае жесткопластичной связи его с грунтом по формуле (2.62)
Ν кр = 4,09 11 (31,5 10−3 )2 (18,175 10−3 )4 (0,039)2 (2,1 105 )5 (4,94 10−3 )3 =
=17,37 МН.
13.Проверяем выполнение условия (2.60)
8,466 ≤0,9·17,37; 8,466 МН<15,633 МН Условие выполняется, следовательно, устойчивость трубопровода при заданных параметрах обеспечивается.
14. Проверим выполнение условия (2.60) в случае упругой связи прямолинейного трубопровода с грунтом, для чего рассчитаем критическую продольную силу по формуле (2.91)
Ν кр = 2
2 1,02 2,1 105 4,94 10−3 = 92 МН.
8,466 ≤0,9·92 8,466 МН < 82,8 МН.
Как видим, условие устойчивости также выполняется.
15.Расчетная длина волны выпучивания по формуле (2.92)
λкр = 2π 4 2,1 105 4,94 −3 / 2 1,02 = 29,8 м.
16.Для оценки устойчивости упругоизогнутого участка трубопровода определим параметры θ и Z по формулам (2.70) и (2.71)
θ = |
|
|
1 |
= 0,0385. |
|
|
18,175 10−3 |
||
|
1000 |
3 |
|
|
|
2,1 105 4,94 10−3 |
|
||
|
|
|
|
|
|
31,5 10−3 0,039 |
|
||
Z = |
18,175 10−3 4,94 10−3 |
=142,4 . |
||
|
3 |
|
17,175 10−3 |
|
|
2,1 105 4,94 10−3 |
|
||
азатем, используя номограмму (см. рис.2.7), найдем β =19,5.
17.Критическое усилие по формуле (2.68)
Ν кр =19,5 3 (18,175 10−3 )2 2,1 105 4,94 10−3 =13,645 МН. 18. Проверяем условие (2.60)
137
8,466 ≤0,9·13,645 8,466 МН < 12,281 МН,
т.е. условие устойчивости выполняется.
19.Критическое усилие по формуле (2.69)
Νкр = 0,375 18,175 10−3 1000 = 6,816 МН.
20.Проверяем условие (2.60)
8,466 ≤0,9·6,816 ; 8,466 МН >6,134 МН,
т.е. условие устойчивости не выполняется.
Для того, чтобы обеспечить устойчивость трубопровода, следует либо увеличить qв (например, увеличив глубину заложения трубопровода), либо принять больший радиус упругого изгиба трубопровода.
Например, при ρ = 1400 м
Nкр = 0,375 18,175 10−3 1400 = 9,542 МН Условие устойчивости
8,466 ≤0,9·9,542 8,466 МН <8,588 МН,
т.е. условие устойчивости выполняется.
Пример 2.4. Проверить устойчивость прямолинейного участка газопровода III категории, уложенного в песчаной насыпи на болоте II типа.
Исходные данные: Dн = 1,02 м; δн = 12,3 мм; F=0,039 м2; I=4,9410-3 м4; qтр=3683 Н/м; р=7,4 МПа; ∆t = 60 °С; S=8,466 МН; γгр= 16 кН/м3; ϕгр = 36 °С;
сгр=0; размеры насыпи по рекомендациям табл. 2.13: hо= 1 м; h1=Dн= 1,02 м;
Н= 2,2 м; в = 0,85 м; откос 1:m = 1:1,25; αн= 39°.
|
|
Решение |
|
||||
1. Размер h2 по формуле (2.76) |
|
|
|
|
|
||
° |
|
|
o |
|
36o |
|
|
h2=1,02-(0,85+1·ctg 39 |
|
45 |
|
− |
|
|
=0,21 м. |
-0,5 1,02)tg |
|
2 |
|
||||
|
|
|
|
|
|
|
|
2. Среднее давление грунта насыпи на уровне верхней образующей трубопровода по формуле (2.77)
ргр = 0,8 16000 1(0,85 + 0,5 1 сtgo39o )=8990 Па =8,99 10-3 МПа. 0,85 +1 ctg39
3.Пассивное сопротивление грунта по формуле (2.74)
|
|
0,8 16000(1,022 − 0,212 ) |
|
|
o |
|
36o |
|
|
o |
|
36o |
|
|||
Е1 |
= |
|
|
|
45 |
|
+ |
|
|
|
45 |
|
+ |
|
|
= |
|
|
|
|
|
|
|||||||||||
2 |
|
tg |
|
2 |
|
+ 8990 1.02 tg |
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
=59882 Н/м = 59,88 10-3 МН/м.
4.Активное сопротивление грунта по формуле (2.79)
138