Добавил:

euroduck97 ac3402546@gmail.com Направление обучения: транспортировка нефти, газа и нефтепродуктов группа ВН (Вечерняя форма обучения) Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Российский государственный университет нефти и газа им. И.М. Губкина

Предмет:

Основы проектирования и строительства трубопроводных систем

Файл:

Tipovye_raschyoty_pri_sooruzhenii_i_remonte

.pdf

Скачиваний:

320

Добавлен:

01.06.2021

Размер:

18.76 Mб

Скачать

☆

<<< < Предыдущая 3 4 5 6 7 8 9 10 11 12 13 1415 / 8315 16 17 18 19 20 21 22 23 24 25 26 27 > Следующая >>>

Εакт =	0,8 16000 1,02	2		45o −	36	o		45o −	36	o
Εакт =	0,8 16000 1,02		tg 2	45o −	36		+ 8990 1,02 tg 2	45o −	36		=
	2				2				2

=4109Н/м = 4,109 103 МН/м.

5.Сила трения трубы о грунт по формуле (2.75)

Ε2 = 3683 tg36o = 2676Н/м = 2,676 10−3 МН/м.

6.Сопротивление горизонтальным поперечным перемещениям трубопровода

qгор = Ε1 − Εакт + Ε2 = 59,68 10−3 − 4,109 10−3 + 2,676 10−3 = 58,447 10−3 МН/м.

7.Предельные касательные напряжения по формуле (2.64)

τпр =8990 tg36o + 0 = 6532Па = 6,532 10−3 МПа.

8.Сопротивление грунта продольным перемещениям трубопровода по формуле (2.63)

ро =π 1,02 6,532 10−3 = 20,93 10−3 МН/м.

9. Критическое усилие по формуле (2.72)

Ν кр = 3,9711 (20,93 10−3 )2 (58,447 10−3 )4 (0,039)2 (2,1 105 )5 (4,94 10−3 )3 =

=23,94 МН.

10.Проверяем условие (2.60)

8,466<0,9·23,94 8,466 МН <21,546 МН,

т.е. условие выполняется, следовательно, устойчивость наземного трубопровода при заданных размерах насыпи обеспечивается.

Пример 2.5. Проверить устойчивость трубопровода в насыпи с размерами, приведенными в предыдущем примере, на участке поворота в горизонтальной с ρ = 1400 м; fтр =0,3.

139

Решение

1.Половина ширины насыпи понизу по формуле (2.82)

а= 0,85 + tg239,2o = 3,57 м.

2.Сопротивление сдвигу по формуле (2.81)

qсдв = 0,8 16000 tg36o 2,2 (2 3,57 −1,02)+ (2 0,85 −1,02) + 4

+0,3[3683 + 0,8 16000 1,02(2,2 −1,02)]= 40507Н/м = 40,507 10−3 МН/м.

3.Проверяем условие устойчивости (2.80)

40,507·10-3 ≥	1,25 8,466	;	40,507·103 МН/м > 7,559·10-3 МН/м,
	1400

условие устойчивости выполняется.

Пример 2.6. Проверить устойчивость трубопровода в насыпи с размерами, рассчитанными в предыдущих примерах, на участке поворота в

вертикальной плоскости с ρ =1400 м и αв = 50o , qв=18,175·10-3 МН/м.

Решение

1.Длина криволинейного участка по формуле (2.87) lкр = 2 1400 sin 502 =1183 м.

2.Стрела изгиба трубопровода в пределах криволинейного участка по формуле (2.88)

f=1400 − 14002 − 11834 2 =131м.

3.Проверяем условие (2.84)

18,175 10−3	≥	2 1,25 8,466			.
18,175 10−3	≥				.
		1183 1 +	1	1183	2
		1183 1 +	16
			16	131

140

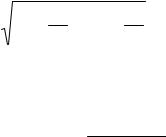
18,175·10-3 МН > 7,246·10-3 МН.

Условие устойчивости трубопровода обеспечивается. 4. Расчетный коэффициент kα по формуле (2.86)

kα = sin2 502 + cos4 502 = 0,92.

5. Проверяем условие (2.85)

18,175 10−3 ≥ 1,25 8,466 ; 0,92 1400

18,175·10-3 МН >8,216·10-3 МН.

Условие выполняется.

Пример 2.7. Определить полное перемещение свободного конца рассматриваемого отрезка трубопровода, построив эпюры распределения перемещений касательных напряжений и продольных усилий по длине трубопровода.

Исходные данные: Dн = 1,02 м; δн = 12,3 мм; F=0,039 м2; σкц=329,4 МПа; ∆t = 60 °С; γгр = 16 кН/м3; ϕгр = 36 °С; сгр=0; ku=8,0 МН/м3 ; hо= 1 м.

Решение

1.Эквивалентное продольное усилие по формуле (2.96)

Р=(0,2·329,4+1,2·10-5·2,1·105·60)·0,039=8,466 МН.

2.Определяем нагрузку от собственного веса трубопровода с учетом

коэффициентов надежности по нагрузке nс.в=1,0 для расчета qпр, используя результаты вычислений из примера 2.3.

qм = nс.вqмн =1,1 3061,5 = 3368 Н/м, qиз = nc.вqизн =1.1 45 = 50 Н/м, qпр = nс.вqпрн =1,0 770 = 770 Н/м, qтр = 3368 +50 + 770 = 4188 Н/м.

141

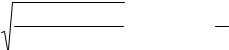
3. Подсчитываем по формуле (2.65) среднее удельное давление на единицу поверхности контакта трубы с грунтом с учетом коэффициента nгр=1,2

		+	1,02			+	1,02		2	45	o	−	36o	+ 4188
	2 1,2 16000 1,02 1,0	+	8		+ 1,0	+	2	tg		45		−	2	+ 4188
			8				2						2

ргр =															=
ргр =				π 1,02											=
				π 1,02

=19880Па =19,88 10−3 МПа.

4.По формуле (2.49) определяем предельные касательные напряжения

τпр =19,88 10−3 tg36o + 0 =14,44 10−3 МПа.

5.По формуле (2.63) ро

ро =π 1,02 14,44 10−3 = 46,28 10−3 МН/м.

6. Параметр β по формуле (2.100)

β =	π 1,02 8,0		= 5,6 10	−2	1	.
	2,1	105 0,039			м

7. Предельная величина продольного усилия по формуле (2.107)

Р	пр	=	14,44 10−3	5,6 10−2	2,1	105 0,039	= 0,828 МН.
Р		=		8,0			= 0,828 МН.

8. Сопоставив величины усилий Р и Рпр

8,466 >0,828 МН,

делаем вывод, что данный пример соответствует расчетной схеме (см. рис.2.15), согласно которой рассматриваемый отрезок трубопровода включает участок упругой связи трубы с грунтом и пластичной связи.

9. Длина участка упругой связи по формуле (2.103)

l1 = 3,5 / 5,6 10−2 = 62,5 м,

соответственно

βl1 = 3,5; chβl1 =16,5.

142

10. Определим перемещения, касательные напряжения и продольные

усилия в нескольких сечениях участка l1, заменив в формулах (2.97), (2.98) и

(2.99) Р на Рпр.

При х=0, u(x)=0, τ(x) = 0

				P (x) = 0,828				1	= 0,05 МН.
				P (x) = 0,828					= 0,05 МН.
						16,5
	При х=10 м
		u(x)=		0,828 0,59						= 0,065	10−3 м = 0,065 мм;
		u(x)=								= 0,065	10−3 м = 0,065 мм;
			5,6 10−2 2,1 105 0,039 16,5
			τ(x) = 8,0 0,065 10−3 = 0,52 10−3 МПа;
				Р(x) = 0,829			1,161		= 0,058 МН.
				Р(x) = 0,829					= 0,058 МН.
						16,5
Результаты вычислений для остальных сечений занесены в табл. 2.17.
													Таблица 2.17
	Результаты вычислений u(x), τ(х) и Р(x) на участке упругой связи
					трубопровода с грунтом
												Касательные
х,м		βх	Гиперболические			Продольные						Касательные	Продольные
х,м		βх	функции			перемещения						напряжения	усилия
			sh βх		ch βх			u(x), мм				τ(x) ·103,МПа	Р(x), МН
												0
0		0	0		1				0			0	0,05*
10		0,56	0,590		1,161	0,065						0,520	0,058
20		1,12	1,369		1,696	0,150						1,200	0,085
30		1,68	2,942		3,108	0,322						2,576	0,155
40		2,24	4,649		4,756	0,509						4,072	0238
50		2,80	8,192		8,253	0,896						7,168	0,413
60		3,36	14,396		14,433	1,575						12,600	0,722
62,5		3,50	16,5		16,5	1,805						14,440	0,828

*) несовершенство расчетной модели.

11. Длина участка пластичной связи трубопровода с грунтом по формуле

(2.110)

143

l2	=	8,466 − 0,828	=165 м.
		46,28 10−3

Таблица 2.18

Результаты вычислений u(x) и P(x) на участке пластичной связи

трубопровода с грунтом

х, м	Продольные усилия	Продольные
	Р( xn ) , МН	перемещения
		u(xn ) , мм
0	0,828	1,805
40	2,679	10,37
80	4,530	27,98
120	6,382	54,62
160	8,233	90,31
165	8,466	95,5

Примечание: Касательные напряжения постоянны по длине и равны предельным.

12. Продольные усилия и перемещения в нескольких сечениях участка l2

определяем по формулам (2.111) и (2.112).

При хn=0 u(xn ) определим по формуле (2.104) как при Р=Рпр

u(x	n	)=			0,828			th5,6 10−2	62,5 =1,805 10−3	=1,805 мм.
				−2		5
		5,6	10		2,1 10		0,039

При этом касательные напряжения максимальны и равны предельным: τmax =τпр =14,44 10−3 МПа.Продольные усилия в том же сечении Р(xn ) равны

Рпр, т.е. Р(xn ) = Рпр=0,828 МН.

При хn= 40 м

Р(xn ) =0,828+(46,28·10-3) ·40=2,679 МН.

u(xn ) = 14,44 10−3	+	0,828 40	+	46,28 10−3 402	=10,37 10−3 м =10,37 мм.
		2,1 105 0,039		2 2,1 105 0,039
8,0

Результаты вычислений для остальных сечений занесены в табл. 2.18.

144

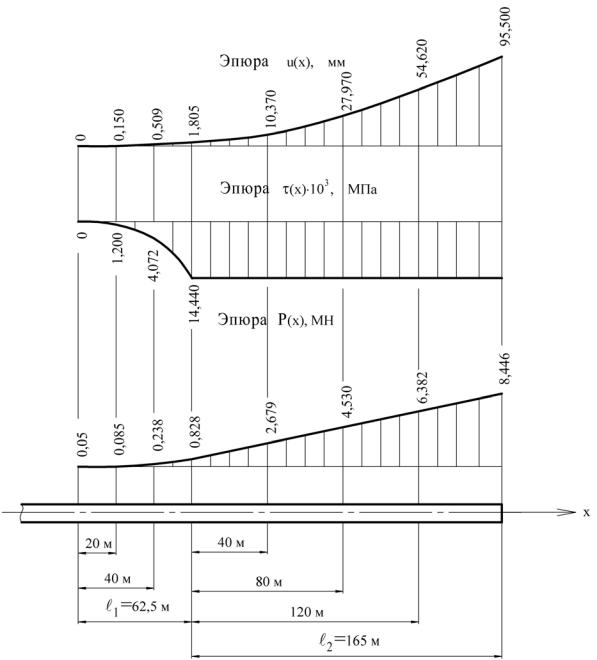
Рис.2.25. Эпюры распределения u(x), τ(x) и P(x) по длине при упругопластичной связи

13. Полное перемещение свободного конца участка трубопровода вычисляем по формуле (2.114)

u =	14,44 10−3	+	8,4662 − 0,8282		= 95,5 10−3	м = 95,5 мм.
	8,0		2π 1,02 14,44 10−32,1 105
				0,039

145

На рис.2.25 изображены эпюры распределения свободных перемещений касательных напряжений и продольных усилий по длине участка трубопровода, рассчитанные в этом примере.

Пример 2.8. Рассчитать отвод от газопровода диаметром Dн=1,02 м и давлением p =7,4 МПа.

Исходные данные:

Dн.от=Dн, радиус

изгиба оси

отвода R=1,5 м;

R1от =R1=395,6 МПа, коэффициент надежности по нагрузке np=1,1.

Решение

Коэффициент несущей способности отвода по табл. 2.16 при

отношении

=1,5, ηот =1,15.

Dн

Расчетная толщина стенки отвода по формуле (2.125)

δот =

1,1 7,4 1,02

1,15 = 0,01182м

=11,82 мм.

2( 395,6 +1,1 7,4 )

По сортаменту на трубы ближайшая

большая толщина δн.от =12,3 мм.

Соответственно Dвн.от=1020-212,3=995,4 мм.

Кольцевые напряжения по формуле (2.123)

σкц

1,1 7,4 0,9954

= 329,4 МПа.

2 0,0123

Максимальные напряжения в отводе по формулам (2.122) и (2.124)

σmax = 324,4

4 1,5 −1,02

= 414,2 МПа;

1,5 − 2 1,02

σmax = 329,4 1,15 = 378,8 МПа.

Пример 2.9. Рассчитать тройник с усиливающими накладками, в котором диаметр магистрали Dнм=1020 мм, диаметр ответвления Dно=530 мм, прочностные характеристики стали марки 10Г2ФБЮ для магистрали R1м=395,6

МПа и стали марки 13ГС R1н = 510МПа, для отвода.

146

Решение

1. Расчетное сопротивление металла отвода по формуле (2.34)

R	=	510 0,9	= 342,5 МПа .

1о		1,34 1

2.Коэффициент несущей способности тройника ηТ =1,03 (рис.2.19).

3.Расчетная толщина стенки магистрали согласно формулы (2.127)

δм =	1,1 7,4	1,02	1,03 = 0,01059м =10,59 мм.
	2( 395,6 +	1,1 7,4 )

Принимаем номинальную толщину стенки магистрали тройника

δнм =11,3 мм.

4.Расчетная толщина стенки ответвления в соответствии с формулой

(2.128)

δо = 0,0113 395342,,65 10,,0253 = 0,00508 мм.

Принимаем номинальную толщину стенки ответвления тройника δно = 7мм.

Пример 2.10. Рассчитать эллиптическую заглушку для трубопровода с наружным диаметром Dн=1,02 м. Расчетное сопротивление стали R1Д=395,67 МПа, рабочее давление р=7,4 МПа, коэффициент надежности по нагрузке np=1,1, общая высота Н=0,41 м.

Решение

1. Расчетная толщина стенки заглушки по формуле (2.149)

	δдн =	1,1 7,4 1,02	= 0,01028 м ,
	δдн =	2(395,6 +1,1 7,4)	= 0,01028 м ,
		2(395,6 +1,1 7,4)
округляем	до	ближайшего	номинального	значения

δн.дн = 0,0103м =10,3 мм.

2.Меридиональные и кольцевые напряжения рассчитаем по формулам

(2.150) и (2.151)

147

σн = 7,4 0,9994 =179,5 МПа; м 4 0,0103

σкцн	=	7,4 0,9994					= 348,5 МПа.
σкцн	=				0,9994	2	= 348,5 МПа.
						2

		4 0,0103	2	−
		4 0,0103	2	−		2
					4 0,41

Пример 2.11. Определить радиусы упругого изгиба трубопровода на поворотах в горизонтальной и вертикальной плоскостях.

Исходные данные:Dн = 1020 мм; δн = 12,3 мм; qтр = 3418 Н/м; I = 4,94·10-3 м4; σи = 90 МПа; В = 1,52 м; α= 1о-5о; l= 36 м × 3 = 108 м.

Решение

1. Минимальный радиус упругого изгиба из условия прочности при повороте:

• в горизонтальной плоскости по формуле (2.155)

ρгор ≥	3 2,1 105		1,02	=1785 м;
	4	90

•в вертикальной плоскости на вогнутом рельефе местности по формуле

(2.161)

ρвог ≥	3 2,1 105		1,02	=1428 м;
	5	90

•в вертикальной плоскости на выпуклом рельефе местности по формуле

(2.163)

ρвып

≥

2,1 105

1,02

=1190 м .

2 90

2. Усилие, необходимое для изгиба трубопровода в горизонтальной

плоскости, по формуле (2,157)

17852 −1082 )

Р =

3 2,1 105

4,94 10−3 (1785 −

= 8,08

−3

МН.

1083

148

<<< < Предыдущая 3 4 5 6 7 8 9 10 11 12 13 1415 / 8315 16 17 18 19 20 21 22 23 24 25 26 27 > Следующая >>>

Соседние файлы в предмете Основы проектирования и строительства трубопроводных систем

#
01.06.202118.76 Mб320Tipovye_raschyoty_pri_sooruzhenii_i_remonte.pdf
#
01.06.202138.43 Mб20ВСТО трубопроводная система.ppt
#
01.06.20216.05 Mб56Описание технологических объектов транспорта газа.pdf
#
01.06.20215.41 Mб38Проектная документация Лукойл-Западная Сибирь.pdf
#
01.06.202114.36 Mб40Проектная документация Северный поток 2.pdf
#
01.06.202114.36 Mб30Северный поток-2.pdf