Добавил:

Eugene_kk Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный университет пищевых технологий

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Book_2016_Liubchyk_Vyshcha_matemat_teoriia_funkts

.pdf

Скачиваний:

Добавлен:

26.03.2021

Размер:

2.37 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 158 9 10 11 12 13 14 15 > Следующая >>>

При фіксованому значенні z0 E ряд (16.5) буде звичайним числовим рядом вигляду (16.1).

О зн а ч е н н я 16.2. Функціональний ряд (16.5) називається збіжним в області Е , якщо при будь-якому z E відповідний йому числовий ряд збігається.

Якщо ряд (16.5) збігається в області Е , то в цій області можна визначити однозначну функцію f (z) , значення якої в кожній точці області Е

дорівнює сумі відповідного числового ряду (16.5) в області Е .

Для функцій комплексної змінної найбільш цікавими є степеневі

ряди, для яких U	n	(z) C	(z z	0	)n , де C – деякі комплексні числа, а
	n	n		0	n
z0 – фіксована точка комплексної площини.

Члени ряду		Cn (z z0 )n			є аналітичними функціями на всій
		n 0

комплексній площині, тому для дослідження властивостей даного ряду можна застосовувати попередні твердження.

Для означення області збіжності степеневого ряду суттєвою вияв-

ляється наступна теорема.
Тео рема 16.1 (т еорема Абеля ) .		Якщо степеневий ряд

Cn (z z0 )n					(16.6)
n 1
збігається при деякому значенні	z z0 , то він збігається,				і причому
абсолютно, при всіх значеннях z , для яких			z z0	z1 z0	. Якщо ряд
абсолютно, при всіх значеннях z , для яких			z z0	z1 z0	. Якщо ряд
(16.6) розбігається при z z2 , z2	z0 , то	він розбігається			при будь-

якому значенні z , для якого	z z0	z2 z0	.


З теорії степеневих рядів відомо, що всередині області збіжності
вони збігаються рівномірно,	тобто їх можна почленно інтегрувати і

диференціювати будь-яке число раз, причому область збіжності при цьому не зміниться.

Область збіжності ряду (16.6) – цє круг з центром в точці z0 .

Радіус збіжності степеневого ряду визначається за формулами:

R lim

(Cn 0) ,

(16.7)

n 1

або

(16.8)

lim n

якщо відповідні границі існують.

Формулу (16.8) часто називають формулою Коші-Адамара. Всередині круга збіжності степеневий ряд збігається до аналітичної функції f (z) . Коефіцієнти степеневого ряду (16.6) виражаються через значен-

ня суми ряду f (z) та її похідних у центрі кола збіжності за формулами

C	1	f (n) (z		) .	(16.9)
			0
n	n!

Таким чином, степеневий ряд всередині круга збіжності визначає аналітичну функцію. Природно поставити питання: чи можна будьякую функцію, аналітичну в крузі радіуса R , зобразити у вигляді степеневого ряду, що до неї збігається?

Тео рема 16.2 (т еорема Те йлора ) . Будь-яка функція f (z) ,

аналітична всередині круга z z0 R , може бути зображеною в цьому крузі збіжним до неї степеневим рядом:


f (z) Cn (z z0 )n .	(16.10)

n 0

На практиці, якщо це можливо, використовують відомі розклади в ряд Тейлора елементарних функцій. Наприклад, такі:

ez 1 z

...

(16.11)

n 0

cosz 1

... (1)n

(16.12)

(2n)!

n 0

(2n)!

sin z z z

... (1)n

(1)

...

(16.13)

2n 1

(2n 1)!

n 0

(2n 1)!

ch z 1

...

(16.14)

(2n)!

n 0

(2n)!

2n 1

sh z z

...

(16.15)

(2n 1)

(2n 1)!

n 0

Розклади 16.11-16.15 мають місце при

Для функцій

ln(1 z)

(1 z)

мають місце наступні розклади в

ряд Тейлора в околі точки z0

0 :

n 1

ln(1 z) z

... (1)n 1

... (1)n

(16.16)

n 0

n 1

( 1)

( 1)( 2)

...

(1 z)

( 1)( 2)...( n 1) zn ... .

(16.17)

Зокрема, при 1 отримаємо:

1 z z2

... (1)n zn

... (1)n zn ,

(16.18)

1 z

n 0

1 z z2 ... zn

... zn

(16.19)

1 z

n 0

Розклади (16.16) – (16.19) мають місце при

(тобто R 1 ).

П р и к л а д 16.2. Розкласти в ряд Тейлора в околі точки z0 0

	f (z)	z
функцію			.
		z2 5z 6

Р о з в ’ я за н н я .

Розкладемо дану функцію на найпростіші дроби:

z2 5z 6 0, D 25 24 1

5 1

5z 6

z1,2

A(z 2) B(z 3)

z 3

(z 3)(z 2)

	z

	(z 3)(z 2)

A(z 2) B(z 3) z .

z 2	B 2 B 2

z 3	A 2

	3	2
f (z)				.
	z 3		z 2

Перетворимо праву частину наступним чином:

f (z)	3			2			1		1		.

	3(1	z	)	2(1	z	)	1	z	1	z
	3(1		)	2(1		)	1		1
	3			2			3		2

Застосовуючи розклад (16.19) функції 1 z , отримаємо:

f (z)

n 0

Ряд

збігається в області

3 ;

n 0

Ряд

збігається в області

2 .

n 0

Таким чином, отриманий ряд збігається в крузі z 2 .

П р и к л а д 16.3.												Розкласти по степенях різниці z 5 функцію
f (z)		1				.

		7 3z
Р о з в ’ я за н н я .
Перетворимо початкову функцію:
f (z)		1									1									1						1		1		.
f (z)																														.
			7 3(z 5						5)			7 3(z 5) 15									22 3(z 5)					22 1	3		(z 5)
																										22 1			(z 5)
																										22
Замінивши в розкладі (16.18)																	z	на			3		(z 5) , отримаємо:
Замінивши в розкладі (16.18)																	z	на		22			(z 5) , отримаємо:
																				22
																								n
	f (z)				1			(1)n				(	3	(z 5))n					1			(1)n		3	(z 5)n
	f (z)							(1)n				(		(z 5))n								(1)n		n	(z 5)n
		22						n 0			22								22 n 0					22
								n
(1)n								3		(z 5)n .
(1)n								22n 1		(z 5)n .
	n 0							22n 1
Цей ряд збігається за умови
				(z 5)			1 або					z 5				22	,
	3
	3
	22														3

тобто радіус збіжності ряду R 223 .

§17. Ряди Лора на

У ряді Тейлора сумування відбувається від 0 до . З’ясуємо, що буде, якщо сумування буде відбуватися від до .

Озна чен ня 17.1. Рядом Лорана називається степеневий ряд вигляду


	Cn (z z0 )n .									(17.1)
	n
Ряд (17.1), очевидно, можна зобразити у вигляді:
							1
Cn (z z0 )n Cn (z z0 )n Cn (z z0 )n
n	n 0					n
					C n
Cn	(z z0 )	n			C n				.	(17.2)
Cn	(z z0 )			(z	z		)	n	.	(17.2)
n 0			n 1	(z	z	0	)
n 0			n 1			0
Ряд

	Cn (z z0 )n									(17.3)

n 0

називається правильною частиною ряду Лорана.

Ряд (17.3) являє собою ряд Тейлора, отже, його область збіжності –

круг з

центром

в точці z0 :

z z0

R1 . Всередині

цього круга ряд

збігається до аналітичної функції

f1 (z) .

Ряд

C n

Cn (z z0 )

(17.4)

)

n 1

називається головною частиною ряду Лорана.

Для означення області

збіжності

ряду (17.4)

зробимо заміну:

, тоді ряд набуває вигляду C n

n . Але це вже звичайний

z z0

n 1

степеневий ряд,

його областю збіжності буде круг радіуса

В цьому крузі ряд збігається до аналітичної функції f2 (z) . Але з

1	випливає, що	z z	R . Отже, ряд по від’ємних степенях
1

R2		0	2
R2

(z z0 ) збігається поза колом радіуса R2 .

Загальною областю збіжності початкового ряду буде переріз областей збіжності рядів (17.3) і (17.4). Якщо R2 R1 , то областю

збіжності ряду (17.2) буде кільце R2 z z0 R1 , де обидва ряди збігаються до аналітичних функцій f1 (z) f2 (z) f (z) . Якщо R1 R2 , то ряд Лорана не має області збіжності.

Розглянемо тепер обернену задачу: чи можна функції f (z) , аналітичній у кільці, поставити у відповідність ряд Лорана?

Те о ре м а 17.1. Будь-яка функція f (z) , аналітична в кільці

R2	z z0	R1 , може бути зображеною у вигляді ряду Лорана (17.1),
R2	z z0	R1 , може бути зображеною у вигляді ряду Лорана (17.1),
де
		Cn	1	f z	dz , n 0; 1; 2;... .
		Cn	2 i C z z0 n 1		dz , n 0; 1; 2;... .
			2 i C z z0 n 1

На практиці при знаходженни коеффиціента Cn намагаються

уникати застосування даної формули, тому що вона може приводити до громіздких обчислень. Для цього, якщо можливо, використовують готові розклади в ряд Тейлора елементарних функцій.

П р и к л а д 17.1. Розкласти функцію f (z)	5z 1	в ряд Лорана

	z2 z 6
по степенях z .
Р о з в ’ я за н н я .
Функція f (z) має дві особливі точки:
z2 z 6 0,
z1 2, z2 3.

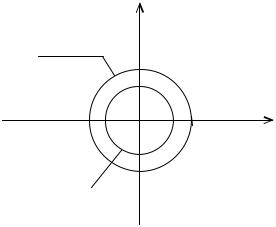
		Отже, є три кільця з центром в точці															z0 0 ,	в кожному з яких
f (z)			є аналітичною функцією (рис. 17.1).
		2,
I)	z	2,
II) 2					z	3,
II) 2					z	3,
				3.
III)		z		3.
										y
							x2 y2		42
									4
									3							III
														II



												I
											0						4	x
											0		1		3		4	x
							x2 y2	32

Рисунок 17.1

Знайдемо ряди Лорана для функції f (z) в кожному з цих кілець.

Зобразимо f (z)

у вигляді суми елементарних дробів.

f (z)

5z 1

A(z 3) B(z 2)

z 2

(z 2)(z 3)

A(z 3) B(z 2) 5z 1.

z 2

A 11

z 3

B 16

f (z)

(17.5)

z 2

z 3

I) Розкладемо початкову функцію в крузі z 2 . Перетворимо її наступним чином:

f (z)	11	16		11			16		11		1		16

	z 2	z 3	2		z	3		z	2			z	3
	z 2	z 3			z			z	2	1		z	3
				1			1
												2

					2			3

Користуючись формулою (16.18), отримаємо:

(

;

n 0

2 ;

n 0

n 0 3

3 .

Підставляючи (17.6) і (17.7) в (17.5) , отримаємо:

5z 1

z 6

n 1

n 0

n 0 2

і область збіжності отриманого ряду –

2 .

Цей розклад є рядом Тейлора функції

f (z)

в крузі

II) Розкладемо

f (z)

у кільці

3 .

Ряд (17.7)

для

1 3z

(17.6)

(17.7)

функції

1		залишається збіжним в цьому кільці, тому що						z	3 . Ряд для
1

1	z
	z

3
функції			1		розбігається для	z	2 .
			1

			1	z
				z

			2

Тому перетворимо													f (z) наступним чином:
									f (z)								11		1						16					1			.										(17.8)

																			1		2					3 1						z
																	z				2											z

																						z								3
Застосовуючи формулу (16.18), отримаємо
											1								2		n								2n
																															.												(17.9)
													2																z	n	.												(17.9)
										1			2				n 0		z							n 0			z
										1			z
Цей ряд збігається для																	2		1 , тобто при																z	2 .


																	z
																	z
Підставляючи (17.9) і (17.7) в (17.8), отримаємо:
					5z 1								11					2n								zn								11 2n					16		zn
f (z)																																					n 1
f (z)		z		2	z				6					z				z	n							n									z		n 1		3			n
		z			z				6					z		n 0		z					n 0		3					n 0					z				3	n 0	3
	11 2n										16					n
															z		.
	z		n 1									n 1			z		.
n 0	z							n 0			3
III) Розкладемо											f (z)				для				z	3 . Ряд (17.9) для функції																					1			буде
																																									1

																																									1		2
																																											2
																																											z
																																											z
збіжним при					z		3 , а для функції																	1				буде розбігатися.
																								1

																						1				z
																										z

																									3
Функцію						f (z)			зобразимо у вигляді:
									f (z)								11		1						16					1				.									(17.10)

																			1		2					z 1						3
																	z				2											3
																						z										z
																						z										z
Користуючись формулою (16.8), отримаємо:
					1						3		n						3n
					1						3		n						3n								3
																						,		де					1							z		3 .					(17.11)
						3														n		,		де				z	1							z		3 .					(17.11)
	1					3			n 0		z						n 0		z									z
	1					z

<<< < Предыдущая 1 2 3 4 5 6 78 / 158 9 10 11 12 13 14 15 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.03.202127.65 Кб0000846.doc
#
26.03.20211.29 Mб05.docx
#
26.03.2021668.28 Кб07.docx
#
26.03.202137.8 Кб07.mcdx
#
26.03.20212.37 Mб1Book_2016_Liubchyk_Vyshcha_matemat_teoriia_funkts.pdf
#
26.03.2021449 б0DEFAULT.DFR
#
26.03.202121.69 Кб3Lab1.docx
#
26.03.202111.88 Кб1laba5.docx
#
26.03.202115.94 Mб2Oglyadovi_lektsiyi_z_teplotekhniki.doc
#
26.03.20213.39 Mб19Teplotekhnika_lektsiyi.doc