Добавил:

Eugene_kk Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный университет пищевых технологий

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Book_2016_Liubchyk_Vyshcha_matemat_teoriia_funkts

.pdf

Скачиваний:

Добавлен:

26.03.2021

Размер:

2.37 Mб

Скачать

☆

<<< < Предыдущая 12 / 152 3 4 5 6 7 8 9 10 11 12 13 14 15 > Следующая >>>

Тоді кожному комплексному числу відповідає один кут вигляду (2.5), він називається головним значенням аргументу.

Виділення такого єдиного кута	часто	буває корисним при
розв’язанні задач. Всі інші значення аргументів z		будемо позначати як
Arg z arg z 2 k , k .		(2.6)
Зобразити комплексне число z x iy	в тригонометричній формі –

це означає знайти модуль z і аргумент за формулами (2.2). Іноді

при знаходженни виникають труднощі. Головне значення визначається за формулами:

				y				x 0;
arctg					;
arctg				x	;
				x
						y
arctg						y	;	x 0; y 0;
arctg							;	x 0; y 0;
						x
							y
arg z arctg								; x 0; y 0;
arg z arctg							x	; x 0; y 0;
							x
		;						x 0; y 0;

	2
			;					x 0; y 0.
			;					x 0; y 0.
		2

arg z

(2.7)

Враховуючи співвідношення (2.6) можна стверджувати, що два відмінних від нуля комплексних числа є рівними між собою, якщо є рівними їхні модулі, а аргументи або рівні, або відрізняються на число, кратне 2 :

		z		z		2	,
		z		z			,
			1
z1 z2						2 k, k .		(2.8)
						2 k, k .
					2
	1				2

П р и к л а д 2.1. Зобразимо в тригонометричній формі наступне комплексне число: z 3 3i .

Р о з в ’ я за н н я .

Цьому комплексному числу відповідає на площині точка A 3;3

або вектор OA (рис. 2.2).

Im z

Re z

Рисунок 2.2

			3 2									– кут,
Маємо:	z		3 2	32				18 3		2 ;		– кут,			який міститься у ІІ
чверті x 0; y 0 , отже
		arctg				3	arctg1								3	.
		arctg				3	arctg1							4	4	.
						3								4	4
			z 3					3	i sin		3
								3			3
Таким чином,				2	cos								.
Таким чином,				2	cos								.
							4				4

П р и к л а д 2.2. Зобразимо в тригонометричній формі наступне комплексне число: z 3 4i .

Р о з в ’ я за н н я .

Зобразимо z на площині точкою B 3; 4 (рис. 2.3) або векто-

ром OB .

Im z

3 0

Re z

B 4

Рисунок 2.3

				3 2					4 2							– кут, який міститься
Маємо:			z	3 2					4 2		9 16 5 ;					– кут, який міститься
в ІІІ чверті x 0; y 0 , отже
										4						4
				arctg						3		arctg					.
				arctg								arctg					.
																3
Таким чином,
					4								4
z	5 cos arctg						i sin arctg
z	5 cos arctg						i sin arctg
					3								3
							4							4
5	cos arctg								i sin	arctg
5	cos arctg								i sin	arctg
							3							3
						4					4
5		cos arctg						i sin arctg
5		cos arctg						i sin arctg
						3					3
					4						4
5		cos arctg						i sin arctg				.
5		cos arctg						i sin arctg				.
					3						3
П р и к л а д 2.3.								Знайти геометричне місце точок,											що зображу-
ють комплексні числа z , для яких															z 1			2 .	(2.9)
ють комплексні числа z , для яких															z 1			2 .	(2.9)

Р о з в ’ я за н н я .

r 2

1 0

Рисунок 2.4

З означення різниці між комплексними числами z і 1 ( z x iy і

1 1 0i , де z – довільна точка шуканої геометричної множини), маємо:

z 1 x 1 iy ,

тоді

z 1 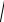x 1 2 y2

і (2.9) можна записати у вигляді

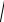x 1 2 y2 2 ,

звідки, після піднесення обох частин до квадрату, отримуємо:

		x 1 2 y2 22 .
Таким чином, множина шуканих точок z					міститься на колі з цен-
тром в точці 1;0	і радіусом r 2 (рис.2.4).
П р и к л а д 2.4.		Знайти, де містяться			точки, що зображують
комплексні числа	z , які задовольняють наступні дві нерівності:
		0 arg z ,			(2.10а)
		6
		0	z 1	1 .	(2.10б)
		0	z 1	1 .	(2.10б)

Р о з в ’ я за н н я .

Для розв’язання задачі знайдемо спочатку множину точок, що задовольняють умови (2.10а) і (2.10б) окремо. А потім серед них виберемо точки, які задовольняють і (2.10а), і (2.10б). За означенням аргументу точки, які задовольняють умову (2.10а), лежати між і на променях

OA (додатний напрям осі OX ) і OB (промень нахилений до додатно-

го напряму осі OX	під кутом	(рис. 2.5).
		6
	y
		B

			6
	0	A	x
		Рисунок 2.5
Точки z , які задовольняють умову (2.10б) лежать всередині круга
з центром в точці	1;0 і радіусом r 1 ,		окрім самого центра, тобто

точки 1;0	(тому що при z 1 маємо	z 1	0 ) (рис. 2.6).
точки 1;0	(тому що при z 1 маємо	z 1	0 ) (рис. 2.6).
	y

Рисунок 2.6

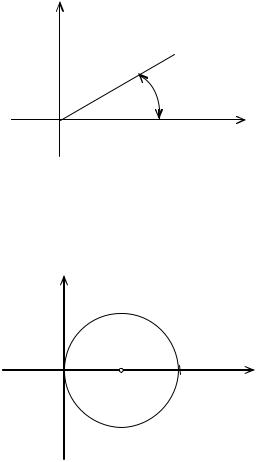
Одночасно умови (2.10а) і (2.10б) задовольняють точки множини, що є перетином множин точок, зображених на рисунках 2.5 і 2.6. Тоді

множина комплексних чисел z , зображених на рис. 2.7, і дає розв’язок задачі.

			A
0	1	2	x

Рисунок 2.7

§3. Дії на д ком плек сн и ми чи слами в т ригономет ричній фо рмі

Якщо комплексні числа зображені в тригонометричній формі, то виконання операцій множення, ділення та добування кореня значно полегшується.

Нехай z1		z1		cos1 i sin 1	і z2		z2		cos2 i sin2 . Користую-

чись означенням добутку комплексних чисел, знайдемо добуток цих чисел:

z1 z2

cos 1

i sin 1 cos 2

i sin 2

cos1 cos2 sin1 sin2

i cos1 sin2 cos2 sin1

cos

i sin

(3.1)

Якщо z2 0 , то для частки цих чисел отримаємо:

cos 1

i sin 1

cos 1

i sin 1 cos 2

i sin 2

cos 2

i sin 2

cos 2

i sin 2 cos 2

i sin 2

cos 1 cos 2 sin 1 sin 2

i sin 1 cos 2 sin 2 cos 1

cos2

sin2

cos

i sin

(3.2)

Як видно з (3.1) і (3.2), добуток і частка двох комплексних чисел виявилися зображеними в тригонометричній формі.

Сформулюємо отримані в формулах (3.1) і (3.2) результати.

1. Модуль добутку двох комплексних чисел дорівнює добутку модулей цих чисел, тобто

z1 z2				z1				z2		.	(3.3)

Одне з значень аргументу добутку двох комплексних чисел дорівнює сумі аргументів множників, тобто

arg z1 z2 arg z1 arg z2 .

(3.4)

Ці ж висновки легко розповсюдити і на добуток якого завгодно числа комплексних чисел, отже

z1 z2 ... zn z1 z2 ... zn ,

arg z1 z2 ... zn arg z1 arg z2 ... arg zn .

2. Модуль частки двох комплексних чисел дорівнює частці їхніх модулей, тобто

0 .

(3.5)

Одне зі значень аргументу частки двох комплексних чисел дорів-

нює різниці аргументів цих чисел, тобто

arg

arg z1 arg z2 .

(3.6)

Застосуємо результати (3.2), (3.3) і (3.4) для обчислення

z n , де

, z 0 . Оскільки натуральний степень числа є добутком рівних

множників, то

zn rn cos i sin n rn cos n i sin n .

(3.7)

Скорочуючи на r n , отримаємо

cos i sin n cos n i sin n .

(3.8)

Це співвідношення відомо як формула Муавра. Формулу Муавра можна узагальнити на випадок, коли n – ціле від’ємне число. Дійсно, якщо n m 0 ( m 0 ), то

cos i sin n				1	1
			cos i sin m		cos m i sin m

	cos m i sin m			cos m i sin m cos m i sin m
	cos2 m sin2	m

cos n i sin n .

Озна чен ня 3.1. Комплексне число називається коренем n -го степеню з числа z , якщо n z .

Покажемо, що в області комплексних чисел операція добування

кореня завжди виконується.
Тео рема 3.1. Якщо z 0 , то існує n	різних комплексних чи-
сел n які є коренями n -го степеню з z . При	z 0 існує єдине число

0 .

Доведення. Нехай z r cos i sin 0 – дане комплексне чис-

ло. Будемо вважати cos i sin таким, що задовольняє умову

n z .

(3.9)

Користуючись формулою Муавра (3.8), подамо умову (3.9) у вигляді

n cos n i sin n r cos i sin .

(3.10)

Запишемо умову (2.8) рівності цих двох комплексних чисел:

n r,

n 2 k,

Звідси знайдемо

nr ,

2 n n

k .

(3.11)

(3.12)

Таким чином,

n r ,

arg

k ,

k .

Тоді шукані значення:

r cos

i sin

k .

(3.13)

Можна показати, що серед нескінченної множини значень k є n

різних чисел. А саме, це ті числа, які отримуються з (3.13) при
k 0;1;2;...;n 1.	(3.14)

Таким чином, теорему доведено, і дано спосіб для обчислення ко-

реня будь-якого степеню з будь-якого комплексного числа. Для цього потрібно зобразити це число в тригонометричній формі і скористатися формулою (3.13) з урахуванням (3.14).

Геометричний результат добування кореня n -ого степеню з комплексного числа зображується точками k комплексної площини,

							2
розташованими на колі радіуса n r на кутовій відстані							2	одне від
розташованими на колі радіуса n r на кутовій відстані							n	одне від
							n
одного,	тобто у вершинах правильного n -кутника, вписаного в коло
	n		. Перша точка має полярні координати n		, ,
радіуса	n	r	. Перша точка має полярні координати n	r	, ,			решта то-
						n

чок міститься на колі послідовно через кут 2n .

П р и к л а д 3.1. Знайти комплексні розв’язання рівняння:

z3 8i 0 .

(3.15)

<<< < Предыдущая 12 / 152 3 4 5 6 7 8 9 10 11 12 13 14 15 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.03.202127.65 Кб0000846.doc
#
26.03.20211.29 Mб05.docx
#
26.03.2021668.28 Кб07.docx
#
26.03.202137.8 Кб07.mcdx
#
26.03.20212.37 Mб1Book_2016_Liubchyk_Vyshcha_matemat_teoriia_funkts.pdf
#
26.03.2021449 б0DEFAULT.DFR
#
26.03.202121.69 Кб3Lab1.docx
#
26.03.202111.88 Кб1laba5.docx
#
26.03.202115.94 Mб2Oglyadovi_lektsiyi_z_teplotekhniki.doc
#
26.03.20213.39 Mб19Teplotekhnika_lektsiyi.doc