Добавил:

Eugene_kk Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный университет пищевых технологий

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Book_2016_Liubchyk_Vyshcha_matemat_teoriia_funkts

.pdf

Скачиваний:

Добавлен:

26.03.2021

Размер:

2.37 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1513 14 15 > Следующая >>>

Обчислимо невласний інтеграл:

			1				p								1				p														A		1						p							1					p
																						dp								lim																									dp
			2		p	2			36						2		p	2	196			dp								lim					2				p	2	36							2		p	2	196			dp
p			2		p				36						2		p		196														p		2				p		36							2		p		196
																														A
		d p2					36 2 pdp pdp																			1				d p2				36
																										1
																										2
		d p2					196 2 pdp pdp																						1		d p2					196
																													1
																													2
	1						A d						p2			36						A d					p2 196
	1			lim																dp																	dp
	4			lim							p			2	36					dp					p			2		196							dp
	4			A							p				36										p					196
							p															p
	1						ln											A														A			1										p		2		36					A
																																																						A

				lim						p		2				36			ln		p		2	196														lim ln

																																														2			196
	4 A																	p														p				4 A								p					196					p
									A2 36															A2																		1				p2 36								p
																		lim ln										ln1 0															ln
		lim ln
		lim ln						A2 196																A2
		A						A2 196											A					A2																	4				p2 196

1 ln p2 196 .

4 p2 36

Отже:

sin 4t sin10t

196

П р и к л а д 3.11.

Використовуючи

теорему

про

інтегрування

зображення , знайти зображення наступної функції

f t

1 e 7t

Р о з в ’ я за н н я .

У даному випадку

f t

g t

, де

g t 1 e 7t .

З властивості лінійності та формули (3.3) маємо:

1 e 7t	1	1	.

	p	p 7

125

Отже, зображення G p

функції g t

має вигляд:

G p

p 7

За теоремою про інтегрування зображення (3.21):

g t

f t

G p dp .

Обчислимо невласний інтеграл

G p dp :

lim

A dp

lim

p 7

p p

lim ln

p 7

lim ln

A 7

lim ln

ln1 0

A 7

p 7

Остаточно маємо:

1 e 7t ln

p 7

6°. Тео рема 3.6 (теорема про інтегрування оригін ала).

Нехай функція-оригінал

f t

має зображення F p , тоді:

f d

(3.23)

126

Таким чином, інтегрування оригінала зводиться до ділення зображення на p .

П р и к л а д 3.12. Використовуючи теорему про інтегрування

оригінала, знайти зображення наступної функції f t sh 2 d .

Р о з в ’ я за н н я .

Функція	g t sh 2 є оригіналом і задовольняє теорему 3.6.
Нехай G p	– зображення функції g t . Тоді за формулою (3.23):
	f t	G p	.

		p

Знайдемо зображення оригінала g t . Оскільки за формулою (3.6):

2
sh 2t		,
	p2 4

то за теоремою 3.4 про диференціювання зображення (3.20):


								2						1
				1				2
t sh 2t 1															,
t sh 2t 1						p	2		4						,
						p			4

		2	1		2														4 p
		2			2					2 p									4 p			.

	2	4		p2 4					2								p2 4				2
p		4		p2 4													p2 4
Отже:
						t sh 2t													4 p				.

																		p2 4 2
Остаточно маємо:
												4 p

		t							p		2				4	2				4 p					4
									p						4					4 p					4


		sh 2 d																									.
		sh 2 d											p						p	p2 4				2	p2 4	2	.
		0											p						p	p2 4					p2 4

127

П р и к л а д 3.13.

Використовуючи

теорему

про інтегрування

оригінала, знайти зображення наступної функції cos2 5 d .

Р о з в ’ я за н н я .

Підінтегральна функція:

g t cos2 5t . Аналогічно попередньому

прикладу, знайдемо зображення cos2 5t :

cos2 5t

1 cos10t

cos10t ,

cos10t

100

p2 100 p2

p2 50

cos

p2 100

p p2 100

p p2

100

p2 50

p p2 100

p2 50

cos

5 d

100

7°. Тео рема 3.7 (т еорема зсунен ня ).

Якщо

функція-

оригінал

f t має зображення F p

f t F p , то для будь-

якого комплексного

p0 :

e p0t f t F p p0 .

(3.24)

П р и к л а д 3.14.

Знайти зображення наступної функції

f t e t t3 .

Р о з в ’ я за н н я .

Функція t 3 має зображення за формулою (2.8):

t3 3! 6 .

p3 1 p4

128

За теоремою зсунення, враховуючи, що p0 1, остаточно маємо:

e t t3	6		.

	p	1 4
	p	1 4

П р и к л а д 3.15. Знайти зображення наступної функції f t t et cost .

Р о з в ’ я за н н я .

Знайдемо зображення функції t cos t . За формулою (2.5):

										cos t										p				.

																		p2 1
За теоремою про диференціювання зображення (3.20):

									p					1						p						1
					1				p											p
t cos t 1																											,
t cos t 1								p	2	1									p	2							,
								p		1									p		1
				1 p			1			2 p p
	p	1				2											p		2	1 2 p								2	1	p	2
	p																p			1 2 p									1	p				.

	2											2															2						2
p 1																				p2									p
p 1							p2 1													p2		1							p	2 1
Отже:
						t cos t										p2 1							.										(3.25)
						t cos t																2	.										(3.25)
															p2 1
Застосуємо теорему зсунення																	(3.24), де											p0 1 , і з виразу (3.25)
остаточно отримаємо:
		t e	t	cos t									p 1 2 1															p2 2 p				.
		t e		cos t							p 1 2						1 2								p2			2 p 2 2				.

129

8°.	Тео рема 3.8 (теорема запізнення).								Нехай функція-
оригінал	f t має зображення				F p f t F p . Розглянемо
функцію t , визначену наступним чином:
				0,	t t		;
		t				0			(3.26)
		t		f t t			, t t	.	(3.26)
				f t t		0	, t t	.
						0	0

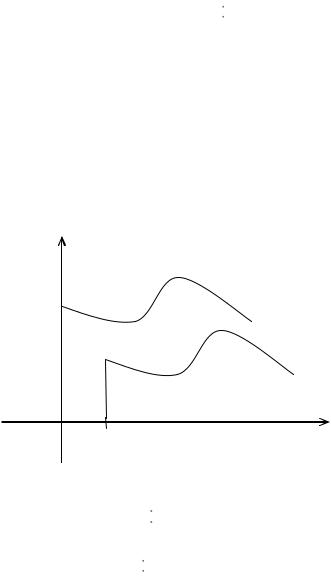
Графік функції t			отримується з графіка оригінала в результаті

зсунення його праворуч вздовж осі OT на величину t0 (рис.3.1). Отже,

якщо f t описує деякий процес, то t описує той же процес, але з запізненням на t0 .

f t

Рисунок 3.1

Тео рема 3.9. Нехай f t F p , тоді для будь-якого до-

датного :

f t t e p 0 F p .

(3.27)

130

П р и к л а д 3.16. Знайти зображення функції f t sin t 2 t 2 .

Р о з в ’ я за н н я .

Оскільки за формулою (2.4)

1
sin t		,
	p2 1

то за теоремою про запізнення сигнала (3.27), враховуючи, що 2 , маємо:

e 2 p sin t 2 t 2 p2 1 .

П р и к л а д 3.17. Знайти зображення функції f t t2 t 1 .

Р о з в ’ я за н н я .

Оскільки маємо запізнення сигнала 1 , то й оригінал повинен залежати від аргумента t 1 . Отже, перетворимо функцію t 2 у функ-

цію від аргумента t 1 :

t2 t 11 2 t 1 2 2 t 1 1.

Враховуючи формулу (2.8), для оригінала t2 2t 1 маємо зображення:

t 2 2t 1	2	2	1	2 2 p p2	.
	p3	p2
			p	p3

Застосуємо теорему про запізнении сигнала (3.27) і запишемо остаточний вигляд зображення :

t 2 t 1 t 1 2	2 t 1 1	t 1	2 2 p p2		e p .

			p	3

131

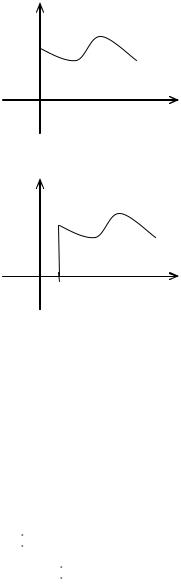
Якщо функція f t при t 0 є оригіналом (рис.3.2а),

f t

Рисунок 3.2а

		0		t
		0		t
			Рисунок 3.2б
то функція t (при	t 0 ) отримується з графіка функції				f t
зсуненням на величину :
			0,	t ;
		t			(3.28)
		t	f	t , t .	(3.28)
			f	t , t .

Тоді, за допомогою функції Хевісайда t , функцію t	можна
перетворити наступним чином:
t f t t .	(3.2
Тоді, якщо f t F p , то за теоремою запізнення:
t e pt F p .	(3.30)

132

Теорема запізнення дає можливість отримати зображення функцій, які описують імпульсні процеси.

Розглянемо зображення одиничного імпульса t , який діє на проміжку (рис.3.3).

Рисунок 3.3

Аналітично одиничний імпульс можна зобразити як:

0, t	0;
	t ;	(3.31)
t 1, 0	t ;	(3.31)
	0.
0, t	0.
За допомогою функції Хевісайда запишемо функцію t :
t t t .		(3.32)
Якщо одиничний імпульс t	починається при t T	і діє в період

часу (рис.3.4), то аналітично такий імпульс

Рисунок 3.4

133

можна зобразити як:
0, t T;
		(3.33)
t 1, T t T ;		(3.33)

0, t T .
Аналогічно виразам (3.32) маємо вираження імпульса (3.33) в
наступному вигляді:
t t T t T .		(3.34)
Розглянемо загальний випадок:
0,	t a1 ;
	t , a1 t a2 ;
f t f1	t , a1 t a2 ;	(3.35)
	t , t a2 ,
f2	t , t a2 ,
де f1 t і f2 t – функції-оригінали.
Використовуючи вираз (3.35), можна записати оригінал		f t од-
ним аналітичним виразом:
f t f1 t t a1 f1 t t a2 f2 t t a2 .		(3.36)
П р и к л а д 3.18. Знайти зображення функції
	2t 1, t 2;3 ;
f t
f t	0, t 2;3 .

Р о з в ’ я за н н я .

Враховуючи вираз (3.36), запишемо аналітичний вираз для функції f t :

f t 2t 1 t 2 2t 1 t 3 .

(3.37)

134

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1513 14 15 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.03.202127.65 Кб0000846.doc
#
26.03.20211.29 Mб05.docx
#
26.03.2021668.28 Кб07.docx
#
26.03.202137.8 Кб07.mcdx
#
26.03.20212.37 Mб1Book_2016_Liubchyk_Vyshcha_matemat_teoriia_funkts.pdf
#
26.03.2021449 б0DEFAULT.DFR
#
26.03.202121.69 Кб3Lab1.docx
#
26.03.202111.88 Кб1laba5.docx
#
26.03.202115.94 Mб2Oglyadovi_lektsiyi_z_teplotekhniki.doc
#
26.03.20213.39 Mб19Teplotekhnika_lektsiyi.doc