
Book_2016_Liubchyk_Vyshcha_matemat_teoriia_funkts
.pdf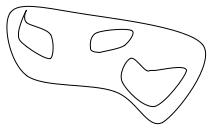
може служити область, межа якої складається з n Жорданових кривих: l1;l 2 ;...;ln (рис. 6.2).
l2 |
l1 |
|
|
l3 |
ln |
|
Рисунок 6.2
О зн а ч е н н я 6.8. Якщо область E целиком міститься всередині деякого круга скінченого радіуса, то вона називається обмеженою. В протилежному випадку – необмеженою.
35
§7. Функці ї ко мпле ксн ої змін ної
Будемо вважати, що на множині E комплексної площини задано функцію комплексної змінної, якщо задано закон, який ставить у відповідність кожній точці множини E деяке комплексне число або сукупність комплексних чисел. Множину E будемо називати множиною значень незалежної змінної. Якщо кожній точці z E ставиться у відповідність точка , то функція називається однозначною, якщо ставиться у відповідність сукупність точок , тоді функція називається багатозначною. Символічно вказану відповідність будемо записувати у вигляді
f z . |
(7.1) |
Множина комплексних чисел , відповідних усім |
z E , нази- |
вається множиною значень функції f z . |
|
Оскільки кожне комплексне число характеризується парою
дійсних чисел, то задання комплексної функції u iv |
комплексної |
|||
змінної z x iy |
є еквівалентним заданню двох функцій дійсних |
|||
змінних, що може бути записано у вигляді |
|
|||
|
z u x, y iv x, y . |
(7.2) |
||
Таким чином, функції u x, y |
і v x, y визначені в деякій області |
|||
площини дійсних змінних |
x і y , |
відповідній до області |
E комплекс- |
|
ної площини z . |
Функція |
u x, y називається дійсною частиною, а |
||
функція v x, y – уявною частиною функції f z .
Геометрична интерпретація поняття функції (7.1) комплексної змінної заключається в тому, що рівністю f z встановлюється
закон відповідності між точками z області E комплексної площини і точками області G комплексної площини. Очевидно, встановлюється і зворотна відповідність – кожній точці G ставиться у відповідність
36
одна або декілька точок z області E . Це означає, що в області G задано (однозначну або багатозначну) функцію комплексної змінної :
z . |
(7.3) |
Функція (7.3) називається оберненою для функції (7.1). Область задання G функції є областю значень функції f z .
Озна чен ня 7.1. Функція f z називається однолистою функ-
цією в області E , якщо в різних точках z цієї області вона приймає різні значення.
37

§8. Основні елеме нт арні фун кц ії компле ксн ої змін ної
8.1. Степенева функція zn . |
|
Степенева функція zn при |
n є однозначною функцією, |
тому що ставить у відповідність будь-якому комплексному числу
zx iy cos i sin 0 число
nein n cos n i sin n .
|
|
|
|
|
|
|
|
|
|
|||||||||
Функція n z |
кожному значенню |
z ставить у відповідність n |
||||||||||||||||
різних чисел |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
i 2 k |
|
|
|
|
|
|
2 k |
|
|
|
2 k |
|
||||
|
|
|
|
|
|
|
|
|||||||||||
n e |
n |
n cos |
|
|
|
|
i sin |
|
|
|
|
; |
||||||
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
n |
|
n |
n |
|
n |
|
||||
k 0,1,..., n 1 ,
тобто, визначає n різних однозначних функцій.
8.2. Показникова функція ez .
Оскільки z x iy , то ez визначається співвідношенням ez ex iy ex cos y i sin y ex cos y iex sin y ,
тобто
Re ez u x; y ex cos y ,
Imez v x; y ex sin y .
Показникова функція володіє наступними властивостями. 1°. Функція є однозначною.
2°. Для дійсних значень z x означення збігається з означенням показникової функції для функцій дійсной змінної.
38
3°. Зберігається основна властивість показникової функції:
ez1 z2 ez1 ez2 .
4°. Показникова функція не обертається в нуль в жодній точці комплексної площини.
5°. В комплексній площині показникова функція є периодичною з суто уявним періодом T 2i :
ez 2 i ez k .
8.3. Логарифмічна функція Ln z z 0 .
Логарифмічна функція Ln z визначається як обернена до по-
казникової функції:
Lnz ln z iArgz ln z i 2 k , k .
1°. Логарифмічна функція Ln z є багатозначною, тому що для будь-
якого z 0 існує нескінченна множина значень Ln z , у яких дійсна ча-
стина u ln z , а уявні частини відрізняються на доданок 2 k .
2°. При k 0 виділяють однозначну функцію ln z : ln z ln z i .
Функцію ln z називають головним значенням функції Ln z .
3°. Для додатних дійсних чисел головне значення логарифма збігається зі значенням логарифмічної функції дійсної змінної і володіє усіми її властивостями.
4°. Зберігаються основні властивості логарифмічной функції:
Ln z1 z2 Ln z1 Ln z2 |
|
z |
|
Ln z1 - Ln z2 ; |
Ln zn n Ln z . |
; Ln |
1 |
|
|||
|
|||||
|
z2 |
|
|
|
|
39

8.4. Тригонометричні функції.
Функції ez ; cos z ; sin z зв’язані формулами Ейлера:
|
|
eiz cos z i sin z ; |
e iz |
cos z i sin z , |
|||||||||||
звідки |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
cos z |
eiz e iz |
|
|
sin z |
eiz e iz |
|||||||
|
|
|
|
|
|
; |
|
|
. |
||||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2i |
|
Функції sin z |
і cos z мають тільки дійсні нулі: |
||||||||||||||
sin z 0 z k ; k |
, |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
. |
|
|
|
|
|||
cos z 0 z 2 k ; k |
|
|
|
|
|||||||||||
Функції tg z і ctg z визначаються рівностями: |
|||||||||||||||
tg z |
sin z |
, |
z |
|
k ; k |
, |
|
|
|
||||||
|
|
|
|
|
|
||||||||||
|
cos z |
|
|
2 |
|
|
|
|
|
|
|
|
|
||
ctg z |
cos z |
, |
z k ; |
k . |
|
|
|
|
|||||||
sin z |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для будь-якого дійсного |
z x |
функції збігаються з тригономет- |
|||||||||||||
ричними функціями sin x , |
cos x , |
tg x і ctg x дійсного аргументу x . |
|||||||||||||
Функції sin z |
і cos z |
– періодичні з дійсним періодом 2 , |
|||||||||||||
а tg z і ctg z |
– з періодом |
. Зберігаються властивості пар- |
|||||||||||||
ності і непарності: |
|
|
|
|
|
|
|
|
|
|
|
|
|||
cos z cos z , |
sin z sin z , |
|
|
|
|||||||||||
tg z tg z , |
ctg z ctg z . |
|
|
|
|||||||||||
Функції комплексної |
змінної |
sin z |
і cos z (на відміну від |
||||||||||||
функції дійсної змінної sin z і cos z ) можуть приймати скільки завгодно більші за модулем значення (тобто больші за одиницю).
40
8.5. Гіперболічні функції.
Гіперболічні функції в комплексній області визначаються рівностями:
sh z |
ez e z |
ch z |
ez e z |
|
|
|
|
|
||||||
|
|
|
|
; |
|
|
; |
|
|
|
||||
2 |
|
|
2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||
th z |
sh z |
|
|
ez |
e z |
; |
cth z |
ch z |
|
ez e z |
. |
|||
ch z |
ez |
e z |
sh z |
ez e z |
||||||||||
|
|
|
|
|
|
|||||||||
Для гіперболічних функцій виконуються всі співвідношення, які зв’язують гіперболічні функції дійсного аргументу. В комплексній площині sh z і ch z є періодичними функціями з суто уявним періодом
2i , а th z і cth z – з періодом i .
Для гіперболічних і тригонометричних функцій мають місце наступні
тотожності: |
|
sin z i sh iz ; sh z i sin iz ; |
tg z i th iz ; th z tg iz ; |
cos z ch iz ; ch z cos iz ; |
ctg z i cth iz ; cth z i ctg iz . |
8.6. Обернені тригонометричні та гіперболічні функції.
Обернені тригонометричні і гіперболічні функції Arcsin z , Arccos z ,
Arctg z , |
Arcctg z , Arsh z , Arch z , Arth z , Arcth z визначаються як |
функції, |
обернені відповідно до функцій sin , cos , tg , ctg , |
sh , ch , th , cth . Всі ці функції є багатозначними і виражаються через логарифмічні функції:
Arcsin z i Ln iz 
 1 z2 ; Arsh z Ln z
1 z2 ; Arsh z Ln z 
 z2 1 ; Arccos z i Ln iz
z2 1 ; Arccos z i Ln iz 
 z2 1 ; Arch z Ln z
z2 1 ; Arch z Ln z 
 z2 1 ;
z2 1 ;
Arctg z 2i Ln 11 iziz ; Arth z 12 Ln 11 zz , z 1 ;
Arcctg z 2i Ln zz ii ; Arcth z 12 Ln zz 11 , z 1 .
41

8.7. Загальна степенева функція za . |
|
|
|
Загальна |
степенева функція za , де |
a i |
– будь-яке |
комплексне число, визначається |
|
|
|
|
za ea Ln z , z 0 . |
|
|
Функція багатозначна, а її головним значенням буде |
|
||
|
za ea ln z . |
|
|
8.8. Загальна показникова функція az |
a 0 . |
|
|
Загальна |
показникова функція az |
a 0 , |
визначається |
рівністю |
|
|
|
|
az ez Ln a . |
|
|
Функція багатозначна, її головним значенням буде
az ez ln a .
П р и к л а д 8.1. Зобразити комплексне число в алгебраїчній формі.
Знайти головне значення. Зобразити на комплексній площині Ln 
 3 i .
3 i .
Р о з в ’ я за н н я . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
За означенням: Ln z ln |
|
z |
|
i arg z 2 k , |
k . |
||||||||||||||||
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 ; |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
2 1 2 |
|
|||||||||
z 3 i |
z |
|
3 |
4 |
|
||||||||||||||||
arg z arctg |
1 |
|
. |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
3 |
|
6 |
|
|
|
|
|
|
|
|
|
||||
Отже, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ln |
3 i |
|
|
|
|
||||||||||||
|
|
|
|
ln 2 i |
|
2 k . |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
42
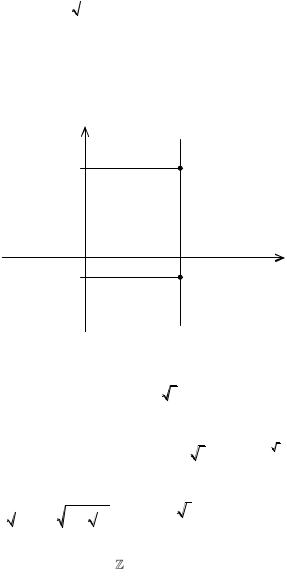
Всі значення |
Ln |
|
i |
зображуються точками, розташованими |
|||||
3 |
|||||||||
на прямій |
x ln 2 |
через проміжки довжиною 2 . Головному значен- |
|||||||
ню |
(при |
k 0 ) |
відповідає |
точка з координатами 0, 7; 0,52 , |
|||||
|
0, 7; |
|
|
|
|
|
|
||
ln 2 |
|
0, 52 . |
|
||||||
|
|
|
6 |
|
|
|
|
||
|
|
|
|
|
|
y |
|
||
|
|
|
|
11 |
5, 75 |
|
|||
|
|
|
|
|
6 |
|
|||
ln 2 0, 7
0 |
x |
0, 52 6
|
|
|
|
|
|
|
|
|
|
|
Рисунок 8.1 |
|
|
|
||
П р и к л а д 8.2. |
|
Обчислити 1 |
3i 2i . |
|
|
|||||||||||
Р о з в ’ я за н н я . |
|
|
|
|
|
|
|
|
|
|
|
|
||||
За означенням: |
az ez Ln a . Маємо: 1 |
3i 2i |
e2i Ln 1 3i . |
|||||||||||||
Обчислимо: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||
Ln 1 3i ln |
12 |
|
3 |
|
i arctg |
2 k |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
k . |
|
|
|
|
|
|||||
ln 2 i |
|
2 k |
|
|
|
|
|
|||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Остаточно маємо:
43

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
||
|
|
|
|
|
|
|
2i |
2i ln 2 |
i |
|
|
|
2 k |
|
2i ln 2 |
|
4 k |
|
|
4 k |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 |
3i |
|
e |
|
|
|
3 |
|
e |
|
3 |
|
e 3 |
|
e2i ln 2 |
|
|||||||||
|
2 |
4 k cos 2ln 2 i sin 2ln 2 , |
|
|
|
|
|
|
|
||||||||||||||||
e 3 |
k . |
|
|
|
|||||||||||||||||||||
Головне значення маємо при k 0 , тобто |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
2i |
|
2 |
cosln 4 i sinln 4 . |
|
|
||||||||
|
|
|
|
|
|
|
|
|
3 |
e 3 |
|
|
|||||||||||||
П р и к л а д 8.3. |
|
Зобразити |
|
в |
|
алгебраїчній |
формі |
||||||||||||||||||
2 |
|
|
|
3i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Arctg |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Р о з в ’ я за н н я .
Скористуємося формулою:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Arctg z |
i |
|
|
Ln |
1 iz |
|
, де z 2 |
3 3i |
, тоді |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
1 iz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
1 i 2 3 3i |
|
|
|
3 i 2 |
|
|
|
3i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
1 iz |
|
|
|
|
3 |
2 3i 3 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
1 iz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 i |
2 |
|
|
3i |
3 2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
2 3 3i |
3i 3 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 i |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3i 6 2 3i |
|
|
|
3i 6 2 3i |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
2 3 |
|
i |
|
|
|
|
|
|
|
|
12 3i 12 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
62 2 |
|
|
2 |
|
|
|
|
|
|
|
36 12 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
6 2 3i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
48 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
1 3i |
|
|
1 |
|
|
|
3 |
i . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
1 |
|
|
|
|
3 |
|
i |
|
1 |
|
|
|
3 |
|
|
|
4 |
|
|
|
1 |
|
|
|
1 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
4 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
16 |
|
|
|
16 |
|
|
|
|
|
4 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 . |
|
|
|
|
|
|||||||||||
arctg |
|
|
4 |
|
|
arctg |
3 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
44
