
Book_2016_Liubchyk_Vyshcha_matemat_teoriia_funkts
.pdf
§14. Теорема Кош і
Значення інтеграла від функції комплексної змінної залежить від напряму інтегрування. Нехай задано область в комплексній площині, обмежену деяким замкненим контуром. Домовимося за додатний приймати такий напрям обходу контура, при якому внутрішня область залишається зліва від напряму руху. Інтегрування в додатному напрямі
будемо позначати як f (z) dz або просто |
f (z)dz , інтегрування у |
С |
C |
від’ємному напрямі – як f (z)dz . |
|
C |
|
Оскільки інтеграл від функції комплексної змінної визначається двома криволінійними інтегралами, то при інтегруванні по замкненому контуру повинні проявлятися властивості криволінійних інтегралів.
Тео рема 14.1 (т еорема Кош и ). Якщо f (z) є однозначною
аналітичною функцією в однозв’язній області Е , то інтеграл від цієї функції по будь-якому замкненому контуру С , який повністю нале-
жить області Е , дорівнює нулю. ( f (z)dz 0) .
С
Теорема Коші встановлює одну з основних властивостей аналітичної функції комплексної змінної.
Cn 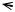 C0
C0
C2
C1
Рисунок 14.1
Теорема Коші формулювалася для однозв’язної області, однак її легко узагальнити й на випадок багатозв’язної області. В цьому випадку повна межа області складається з декількох замкнених контурів:
65
зовнішнього C0 і внутрішніх С1 , C2 ,..., Cn (рис. 14.1). Додатним бу-
демо називати такий напрям обходу повної границі багатозв’язної області, при якому область увесь час залишається зліва. При цьому зовнішній контур обходиться в додатному, а внутрішні – у від’ємному напрямі.
Тео рем а 14.2 (теорема Коши для багатозв’язної області).
|
|
|
|
|
|
|
|
|
|
|
Нехай |
f (z) |
є аналітичною функцією в багатозв’язній області Е , об- |
||||||||
меженій зовні контуром С0 , а зсередини – контурами С , C |
,..., |
Cn . |
||||||||
|
|
1 |
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
Нехай |
f (z) |
– неперервна функція в замкненій області |
|
Е . |
Тоді |
|||||
f (z)dz 0, |
|
|
|
|||||||
де С – повна межа області Е , яка складається з контурів |
||||||||||
С |
|
|
|
|
|
|
|
|
|
|
С0 , С |
, C ,..., Cn , причому обхід границі C відбувається в додатному |
|||||||||
1 |
2 |
|
|
|
|
|
|
|
|
|
напрямі.
66
§15. Інт еграл Кош і
Теорема Коші дозволяє встановити зв’язок між значеннями аналітичної функції у внутрішніх точках області її аналітичності та значеннями на межі.
y
C
r
 z0
z0
0 x
Рисунок 15.1
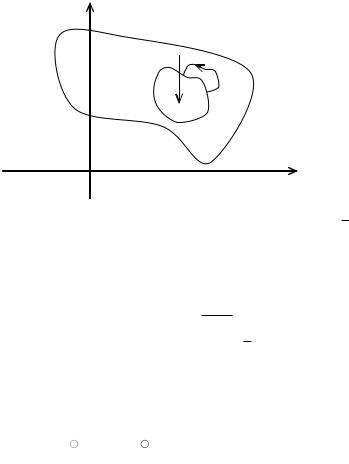
Нехай f (z) є аналітичною функцією в однозв’язній області Е , обмеженій контуром С. Візьмемо довільну внутрішню точку z0 E і
побудуємо навколо неї довільний замкнений контур r , який повністю лежить в області (рис. 15.1).
Розглянемо допоміжну функцію (z) f (z) . z z0
Ця функція буде аналітичною в усій області Е , окрім точки z0 . Якщо ж розглянути двозв’язну область, яка лежить між контуром С і r (рис. 15.1), то в ній (z) буде аналітичною всюди. Згідно з теоремою Коші для двозв’язної області:
|
f (z) |
dz |
f (z) |
dz . |
(15.1) |
||
|
|
|
|
||||
z z |
0 |
z z |
0 |
||||
С |
|
r |
|
|
|
||
Оскільки інтеграли є рівними між собою, не зважаючи на те, що обчислюються по різних контурах, причому r – довільний контур, то вони не залежать від контура.
67

Єдина вимога – точка z0 повинна лежати всередині обох контурів.
Будемо вважати контуром r коло з центром в точці z0 і радіусом : r : z z0 ei , 0; 2 .
|
|
f (z) |
2 |
|
f (z) |
|
|
|
|
2 |
|
|
|||||
|
|
|
|
|
dz |
|
|
|
|
i ei d i f (z)d . |
(15.2) |
||||||
|
z |
z |
|
|
e |
i |
|||||||||||
|
r |
0 |
0 |
|
|
|
|
|
|
|
0 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Інтеграл (15.2) перетворимо наступним чином: |
|
|||||||||||||||
2 |
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
f (z)dz ( f (z) f (z0 ) f z0 )d |
( f (z) f (z0 ))d f (z0 )d |
|||||||||||||||
0 |
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
2 |
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|||
( f (z) f (z0 ))d f (z0 ) |
d |
( f (z) f (z0 ))d f (z0 ) 2 . |
|||||||||||||||
|
0 |
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
Наблизимо теперь до нуля. Оскільки f (z) |
– аналітична функція, |
|||||||||||||||
то вона, відповідно, є неперервною в області |
Е функцією, |
і тому: |
|||||||||||||||
lim f (z) f (z0 ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отже, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
2 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
f (z) |
|
|
d 0 . |
|
|
||||||
|
|
|
|
|
lim |
|
|
f (z |
|
) |
|
|
|
||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
Тому що в формуле (15.1) інтеграли не залежать від контура інтегрування, то можна вибрати як завгодно малим:
f (z) dz i 2 f (z0 ) .
С z z0
Отже,
f (z |
|
) |
1 |
|
f (z) |
dz . |
(15.3) |
|
0 |
|
|
||||||
|
|
2 i |
z z |
|
|
|
||
|
|
|
0 |
|
|
|||
|
|
|
|
C |
|
|
|
|
Формула (15.3) називається інтегральною формулою Коші. Інтегральная формула Коші дозволяє обчислити деякі інтеграли.
68
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e z |
|||
|
П р и к л а д 15.1. |
Обчислити інтеграл |
|
|
|
|
|
dz . |
||||||||
|
|
1 |
|
z2 |
z |
|||||||||||
|
|
|
|
|
|
|
|
|
z 1 |
|
|
|
|
|
|
|
|
Р о з в ’ я за н н я . |
|
|
|
|
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
Контур |
|
z 1 |
|
|
1 |
– коло з центром |
в |
точці z 1 і радіусом |
|||||||
|
|
|
||||||||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
0 |
||
R |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(рис. 15.2). |
|
|
|
|
|
|
|
|
|
|||||||
2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z2 z 0, |
z 0, |
|
|
|
|
|
|
|
|
||||||
|
z(z 1) 0, |
|
|
|
|
|
|
|
|
|
||||||
|
z1 0, |
z2 1. |
|
|
|
|
|
|
|
|
|
|||||
y
z2 1 |
z1 0 |
1 |
|
|
|
|
x |
|
1 |
3 |
|||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
Рисунок 15.2
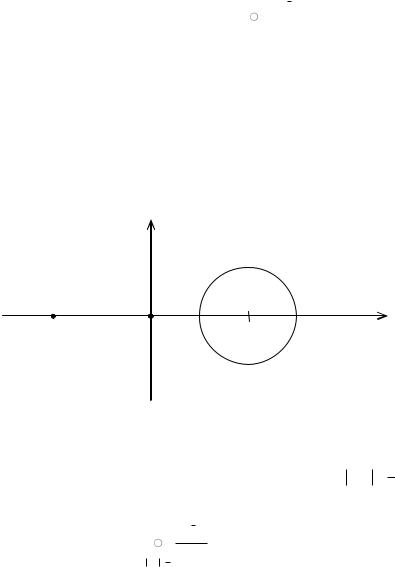
В точках z1 і z2 порушується умова аналітичності функції, але ці точки не потрапляють в область, обмежену контуром С : z 1 12 .
Тому за теоремою Коші
1
ez
1 z2 z dz 0 .
z 1 2
69

П р и к л а д 15.2. |
|
Обчислити інтеграл |
|
ez cos z |
dz . |
|
||||||||||
|
z2 2z |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
z |
1 |
|
|
|
|
Р о з в ’ я за н н я . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Всередині круга |
|
z |
|
1 |
|
x2 |
y2 |
12 |
|
знаменник дробу |
ez cos z |
|||||
|
|
|||||||||||||||
|
|
z2 |
2z |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
обертається в нуль в точці z1 0 (рис. 15.3).
y
z 2 |
z1 0 |
1 |
x |
2 |
|
|
|
Рисунок 15.3
z2 2z 0 z(z 2) 0 z1 0, z2 2
Для застосування формули (15.3) перепишемо інтеграл у наступ-
ному вигляді: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
ez cos z |
dz |
|
ez cos z |
dz 2 i |
ez cos z |
|
|
|||||||||||||||
|
|
|||||||||||||||||||||||
|
z |
2 |
|
2z |
|
|
z 2 |
|
|
|
z 2 |
|
|
|||||||||||
|
z |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
z 0 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 i |
|
e0 cos 0 |
|
2 i |
i . |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Обчислити інтеграл |
|
|
|
dz |
|||||||||
П р и к л а д 15.3. |
|
|
|
. |
||||||||||||||||||||
|
(z2 |
9)(z 9) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
4 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
70
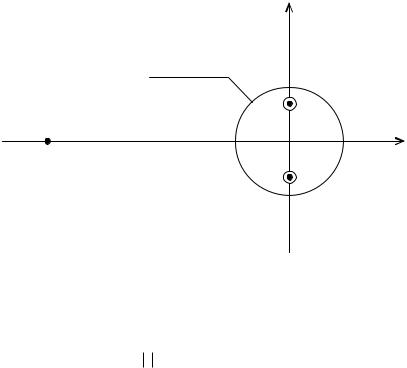
Р о з в ’ я за н н я . |
|
|
|
||||
В області, обмеженій колом |
|
z |
|
4 маємо дві точки: |
z 3i і z 3i , |
||
|
|
||||||
в яких знаменник підінтегральної функції |
1 |
|
обертається в |
||||
|
|||||||
(z2 9)(z 9) |
|||||||
нуль: (z2 9)(z 9) 0 (рис. 15.4). |
|
|
|
||||
z2 9 0, |
z 9 0, |
|
|
|
|
|||||
z2 9, |
|
|
|
|
|
|
|
|||
z1 3i, |
|
z2 3i, |
z3 9, |
|
|
|
|
|||
|
z |
|
4 |
x2 y2 42. |
y |
|
|
|
||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 y2 42 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
r1 |
z1 |
3i |
|
|
|
|
|
|
|
|
|
|
||
|
z3 9 |
|
|
4 |
0 |
|
4 |
x |
||
|
|
|
|
|
z2 |
3i |
|
|||
|
|
|
|
|
|
|
r2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
Рисунок 15.4
Безпосередньо формулу (15.3) застосовувати неможна.
Побудуємо кола r1 і r2 з центрами в точках z1 3i і z2 3i достатньо малих радіусів таких, щоб кола не перетинались і повністю лежали всередині круга z 4 (рис. 15.3).
71

В тризв’язной області, обмеженій колами z 4, r1 і r2 , підінтег-
ральна функція всюди аналітична. За теоремою Коші для багатозв’язной області:
|
|
|
|
|
|
|
|
|
dz |
|
|
|
|
|
|
|
dz |
|
|
|
dz |
|
|
. |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
(z2 |
9)(z 9) |
(z |
2 9)(z 9) |
(z2 9)(z 9) |
|
|||||||||||||||||||||||
|
|
|
|
|
z |
|
4 |
|
|
|
|
|
|
|
|
r1 |
|
|
|
|
|
|
|
r2 |
|
|
|
|
|
|
||||
До кожного інтеграла в правій частині можна застосувати інте- |
||||||||||||||||||||||||||||||||||
гральну формулу Коші (15.3). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
В результаті отримаємо: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
dz |
|
|
|
|
|
(z 3i)(z 9) |
dz |
(z 3i)(z 9) |
dz |
|
|||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
4 |
(z |
|
|
9)(z 9) |
|
|
|
|
z 3i |
|
|
|
|
|
z 3i |
|
|
|
|
|||||||||||||
|
z |
|
|
|
|
|
|
|
|
|
|
r1 |
|
|
|
|
r2 |
|
|
|
|
|
|
|||||||||||
2 i |
|
|
|
|
|
1 |
|
|
|
|
|
|
2 i |
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
(z 3i)(z 9) |
|
|
|
|
|
(z 3i)(z 9) |
z 3i |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z 3i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
9 3i |
|
9 3i |
|
|||||||||||||
2 i |
|
|
2 i |
|
3 |
|
3 |
|
|
|||||||||||||||||||||||||
|
6i(3i 9) |
6i(3i 9) |
92 (3i)2 |
92 (3i)2 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
(9 3i 9 3i) |
|
( 6i) |
i . |
|
|
|
|
|
|
||||||||||||||||||
|
(81 9) |
|
3 90 |
|
|
|
|
|
|
|||||||||||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
45 |
|
|
|
|
|
|
|
||||||||||||||||
72

§16. Степеневі ряди. Формула Коші-Адамара. Ряд Тейлора
Нехай є ряд з комплексними членами:
|
|
z1 z2 z3 ... zn ... zn , |
(16.1) |
n 1
де zn xn i yn .
Озна чен ня 16.1. Ряд (16.1) називається збіжним, якщо збігаєть-
|
n |
ся послідовність Sn його частинних сум |
Sn zk . При цьому гра- |
|
k 1 |
ниця S послідовності Sn називається сумою ряду (16.1). Необхідною умовою збіжності ряду (16.1) є вимога виконання
lim zn 0 .
n
Якщо збігається ряд
|
|
an |
(16.2) |
n1
сдійсними додатними членами, то, очевидно, збігається й ряд (16.1), який в цьому випадку називається абсолютно збіжним. Одним зі способів, що найбільш часто застосовується для дослідження збіжності ряду з комплексними членами, є розгляд ряду з дійсними членами, які є модулями членів початкового ряда. Достатними ознаками збіжності ряду з дійсними додатними членами є ознаки Даламбера і Коші:
Згідно з ознакою Даламбера ряд (16.2) збігається, якщо, починаю-
чи з деякого номера N , виконується нерівність |
an 1 |
|
|
1 для всіх |
|||||
an |
|||||||||
|
|
|
|
|
|
|
|
||
n N . Іншими словами, |
|
|
|
|
|
|
|
|
|
|
an 1 |
|
|
1. |
|
|
|
|
|
lim |
|
|
|
|
(16.3) |
||||
a |
|
|
|
||||||
n |
|
|
|
|
|
|
|
||
|
n |
|
|
|
|
|
|
|
|
73

Згідно з ознакою Коші ряд (16.2) збігається, якщо |
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(16.4) |
|||||||
|
|
|
|
|
|
lim n |
|
a |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Якщо 1 у виразах (16.3) або (16.4), то ряд (16.1) розбігається. |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
in |
|
|
|
||
П р и к л а д 16.1. |
|
Дослідити на збіжність ряд |
e |
. |
|
|
|||||||||||||||||||||||||||||||||||||
|
2 |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
n |
|
|
|
|||
Р о з в ’ я за н н я . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
За формулою Ейлера: ein |
cos n i sin n . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Тоді |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
ein |
|
|
cos n i sin n |
|
|
|
cos n |
|
i |
|
sin n |
, |
|
|
|
|
||||||||||||||||||||||||
n |
n |
2 |
|
|
|
|
|
|
|
|
n |
2 |
|
|
|
|
|
|
|
n |
2 |
|
|
|
|
|
n |
2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
отже |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ein |
|
|
|
|
|
cos n |
|
|
|
|
|
|
sin n |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
||||||||||||
|
|
|
n |
2 |
|
|
|
n |
2 |
|
|
|
n |
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
n 1 |
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Таким чином, питання про збіжність даного ряду зводиться до |
|||||||||||||||||||||||||||||||||||||||||||
питання про збіжність ряду з дійсними членами: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
cos n |
|
|
|
|
|
sin n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
і |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
n |
2 |
|
|
|
n |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
cos n |
|
|
|
|
|
1 |
|
|
|
sin n |
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Враховуючи, |
що |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
і |
|
|
|
|
|
|
|
|
|
|
|
|
, а ряд |
|
|
збігається, |
|||||||||||
|
|
n |
2 |
|
|
|
|
|
n |
2 |
|
|
n |
2 |
|
|
n |
2 |
|
n |
2 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
||||||||||
то кожен з цих рядів збігається абсолютно. Отже, даний ряд збігається абсолютно.
Розглянемо тепер функціональні ряди, членами яких є функції
комплексної |
змінної. Нехай в області Е визначено |
нескінченну |
||
послідовність |
однозначних функцій комплексної змінної |
U |
(z) |
. |
|
|
n |
n 1 |
|
Функціональним рядом будемо називати вираз вигляду: |
|
|
|
|
|
|
|
|
|
|
U n (z) . |
|
(16.5) |
|
n 1
74
