Book_2016_Liubchyk_Vyshcha_matemat_teoriia_funkts

ez

1

ez z 1 1 ez

ez z 11

z ez

1

z 1

2

z 1

2

z 1

2

z

z

2

1 z

1

2

2 z 1 z

z

z

z 1 2z

e

z

e

ez

ez

ez

z 1

2

z 1

4 3

z 1

2

3

z 1

z 1

z

z

1 z

z z z 1 1 z

z

z2

1

e

e

e

z 1 2

z

z

1 3

z 1 3

1 3

lim

1

ez

z2

1

1

e0

1

1

.

z 1 3

z 0

2

2

1 2

Для точки z2

1 маємо:

lim

ez

e 1

z 1 – полюс функції.

z

3 z 1

0

z 1

Визначимо порядок полюса:

lim

ez

z 1 k

при k 1

lim

ez

e 1

1

3 z 1

1 3

z 1 z

z 1 z3

e

z 1 – простий полюс функції.

Враховуючи формулу (19.6), маємо:

Res

ez

1

.

z3 z 1

z 0

e

Підставимо отримані лишки в вираз (20.2) і отримаємо остаточний

результат:

ez

dz 2 i

1

1

2 i

e 2

e 2

i .

3

z 1

z

2

z

2

e

2e

e

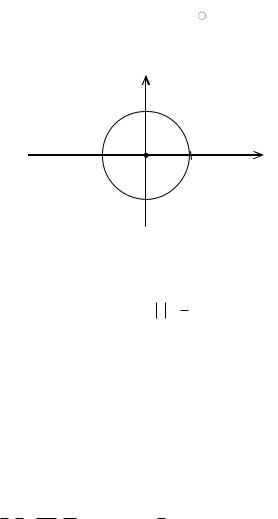
П р и к л а д 20.2. Обчислити інтеграл

z2 sin

1

dz .

z

1

z

Р о з в ’ я за н н я .

2

y

z0 0

1

x

2

Рисунок 20.2

Єдина особлива точка функції f (z) z2

sin

1

– це точка z

0 .

0

z

1

2

2

1

2

точці z0 0 і радіусом

R

x

y

. Оскільки не існує гра-

2

2

ниці lim z2 sin

1

, то

z

0 є істотно особливою точкою.

0

z 0

z

2

1

2

1

1 1

3

1 1

5

1 1

7

z

sin

z

...

z

z

3! z

5! z

7! z

Res z2 sin

1

1

.

z

6

z 0

2

1

2

1

1

i

z

sin

dz 2 i Res z

sin

2 i

.

1

z

z

3

z 0

6

z

2

Обчислити інтеграл

ez

dz .

П р и к л а д 20.3.

z4

2z2

1

z 1

1

Р о з в ’ я за н н я .

Контур інтегрування є колом з центром в точці

z0 i і радіусом

Знайдемо особливі точки підінтегральної функції f (z)

ez

:

z4 2z2 1

z4 2z2 1 0 ;

z2 t t 2 2t 1 0 ;

t 1 2 0 ; t 1 z2 1 ;

z1 i , z2 i

(рис. 20.3).

y

2i

z1 i

0

x

z2 i

ez

ez

dz 2 i Res

.

(20.3)

z4

2z2 1

z i

z4 2z2 1

z i

1

lim

ez

ei

ei

z i

– полюс.

z4 2z2 1

i4 2i2

z i

1

0

lim

ez z i k

lim

ez

z i k

при k 2

z4 2z2 1

z i 2 z i 2

z i

z i

lim

ez

ei

cos1 i sin1

cos1

i

sin1

.

z i 2

2i 2

4

4

4

z i

Отже,

z1 i

– полюс 2-го порядку (k 2) . Тоді за формулою (19.10):

Res

ez

1

lim

d

ez

z i

2

z

4

2z

2

1

dz

4

2z

2

z i

1! z i

z

1

ez

z i 2

ez

z 1 2

ez

z4 2z2

z i 2

1

z i 2 z 1 2

2

z

z

z

1

e z i

2 z i e

e

z i 2

ez

i

2

z i

4 3

z i

3

z

lim

ez

z i 2

ei 2i 2

cos1 i sin1 2i 2

z i

3

2i

3

8i

z i

1

( sin1 cos1 i(sin1 cos1))

i2

( (sin1 cos1) i(sin1 cos1))

4i

4i

i