
7
.docxЛабораторна робота №7
виконав студент групи АК-3-2ск
Козловський Євгеній
Варіант 14
Мета роботи: Опанувати методи золотого перерізу, квадратичної інтерполяції
Знайти екстримальне значення функції
F(x)=-ln(cos(x))-cos(x) [0.5, 0.8]
методами:
золотого перерізу;
квадратичної інтерполяції
Знайти параметр , при якому функція мети досягає мінімального значення
Побудуємо графік функції мети
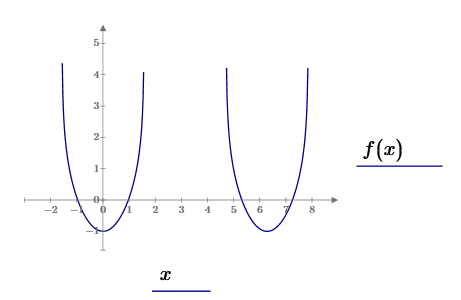
Рисунок 1.1 – Графік функції мети
Мінімум будемо шукати на відрізку [a,b], де
a=-0.2, b=0.2, x=0.1 -початкове наближення
Для знаходження "точного" розв'язку оптимізаційної задачі використаємо стандартну функцію системи MathCad

Рисунок 1.2 – Знаходження "точного" розв'язку оптимізаційної задачі за допомогою програмного забезпечення MathCad
Метод золотого перерізу
Назва даного методу пов'язана з золотим перерізом відрізка [a,b]. Ідея методу така ж, як і в методі дихотомії, тобто відрізок [a,b] ділиться на три частини точками x1 та x2, знаходиться значення функції f(x) в цих точках і визначається, на якому відрізку знаходиться точка мінімуму. Після цього інтервал пошуку мінімального значення функції мети звужується. Але на відміну від метода дихотомії, точки x1 та x2 є точками золотого перерізу відрізка [a,b] і обчислюються за формулами
 Рисунок
1.3 – Знаходження
розв'язку оптимізаційної задачі методом
золотого перерізу за допомогою
програмного забезпечення MathCad
Рисунок
1.3 – Знаходження
розв'язку оптимізаційної задачі методом
золотого перерізу за допомогою
програмного забезпечення MathCad
Метод квадратичної інтерполяції
Ідея методу така: нехай на відрізку [a, b] з внутрішньою точкою мінімуму x*є[a,b] функція f(x) досить добре апроксимується (наближається) многочленом другої степені. Тоді за наближене значення x* доцільно взяти точку мінімуму цього многочлена. Враховуючи цю інформацію, звужуємо початковий інтервал невизначенності [a,b]. Потім до нового, вкороченого інтервалу застосовуємо ту ж процедуру, тобто будуємо новий многочлен другої степені, мінімум якого береться за наступне наближення до точки мінімуму x* функції f(x) і т.д.

Рисунок 1.4 – Знаходження розв'язку оптимізаційної задачі методом квадратичної інтерполяціїза допомогою програмного забезпечення MathCad
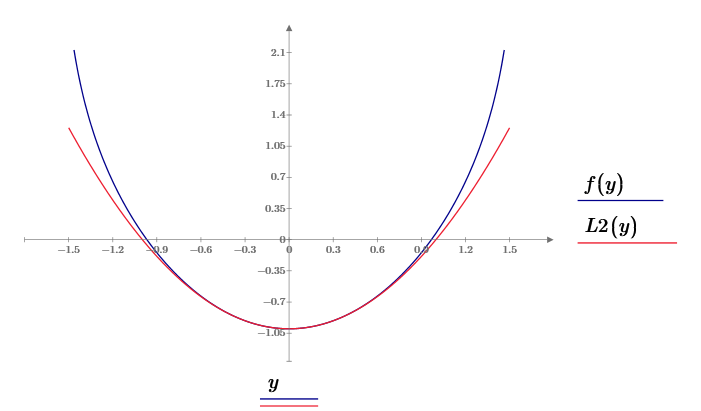
Рисунок 1.5 – Графік функції мети f(x) і полінома Лагранжа L2(x)
Програми
Метод золотого перерізу
#include <iostream>
#include <math.h>
using namespace std;
double f(double i) {
return -log(cos(i))-cos(i);
}
int main() {
system("chcp 1251");
system("cls");
double a=-0.2, b=0.2, x1, x2, f1, f2,e=0.001;
x1 = a+(b-a)*(3-sqrt(double(5)))/2;
x2 = a+(b-a)*(sqrt(double(5))-1)/2;
f1 = f(x1);
f2 = f(x2);
do {
if( f1<=f2) {
b = x2;
x2 = x1;
f2 = f1;
x1 = a+(b-a)*(3-sqrt(5))/2;
f1 = f(x1);
} else {
a = x1;
x1 = x2;
f1 = f2;
x2 = a+(b-a)*(sqrt(5)-1)/2;
f2 = f(x2);
}
} while((b-a)>e);
cout<<"\tРезультат:\n";
cout.precision(4);
cout<<"a="<<a<<"\t\tb="<<b<<endl;
cout.precision(4);
cout<<"f(x1)="<<f1<<"\tf(x2)="<<f2<<endl;
cout<<"Точність: "<<b-a<<endl;
return 0;}

Рисунок 1.6 – Результат виконання програми
Метод квадратичної інтерполяції
#include<iostream>
#include<conio.h>
#include<math.h>
using namespace std;
double f(double x) {
return -log(cos(x))-cos(x);
}
int main() {
system("chcp 1251");
system("cls");
double x1,a0,a1,a2,xx0,xx1=x1=-0.2,x2,x3=0.2,e=0.1,dx=0.01;
x2=x1+dx;
do {
xx0=(x1+x2-a1/a2)/2;
if(f(x1)>f(xx0)&&f(xx0)<f(x2)&&x1<xx0&&xx0<x2) {
x1=xx0;
x2=x2;
x3=x3;
} else if(f(x2)>f(xx0)&&f(xx0)<f(x3)&&x2<xx0&&xx0<x3) {
x1=x2;
x2=xx0;
x3=x3;
}
} while(fabs(xx0-xx1)<e);
cout<<"\tРезультат\n";
cout<<"x*="<<xx1<<"; f(x*)="<<f(xx1);
return 0;
}
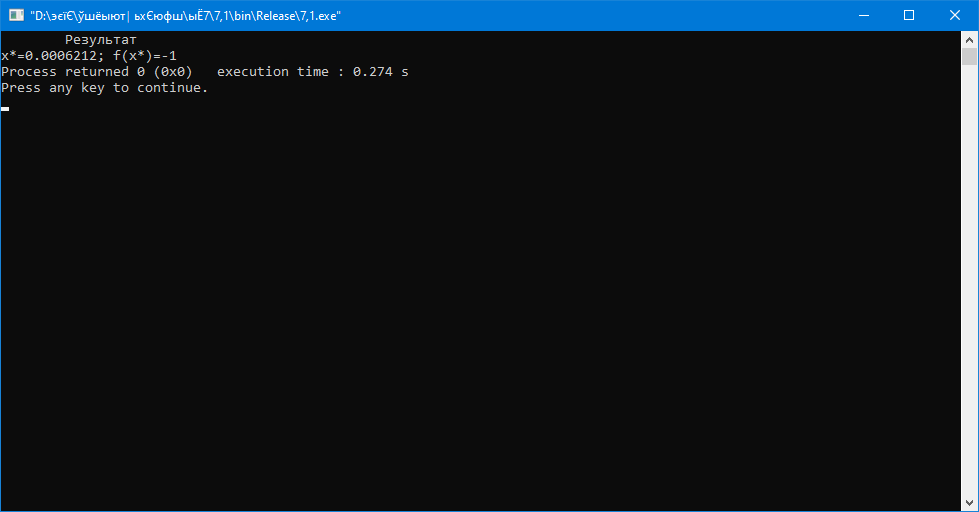
Рисунок 1.7 – Результат виконання програми
Висновок: на даній лабораторній роботі було розв'язано оптимізаційні задачі методом квадратичної інтерполяції та методу золотого перерізу.
