5

Лабораторна робота №5

виконав студент групи АК-3-2ск

Козловський Євгеній

Варіант 14

Мета роботи: Опанувати методи Ейлера, Рунге-Кутта

Знайти наближений розв'язок звичайного диференціального рівняння першого порядку

Знайти наближений (числовий) розв’язок:

1) скалярного диференціального рівняння першого порядку (варіанти рівнянь вибираються з Таблиці 7.1;

2) системи звичайних диференціальних рівнянь (варіанти систем вибираються з Таблиці 7.2;

Всі завнання виконати двома методами:

1. методом Ейлера;

2. методом Рунге-Кутта

та побудувати графіки одержаних розв’язків

Знайти наближений розв'язок звичайного диференціального рівняння першого порядку

Знайдемо спочатку "точний" розв'язок диференціального рівняння за допомогою однієї із стандартних функцій системи MathCad.

Для цього задамо величину   - кількість елементарних відрізків, на які поділяється відрізок інтегрування [x0,xk].

( чим більше  , тим вища степінь точності розв'язання диференціального рівняння)

- метод Рунге-Кутта з фіксованим кроком

Рисунок 1.1 – Обчислення "точного" розв'язку диференціального рівняння за стандартних функцій системи MathCad.

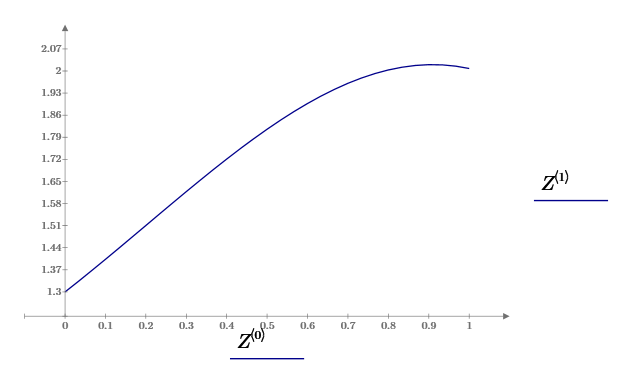
Рисунок 1.2 – Графік "точного" розв'язку   звичайного диференціального рівняння

Метод Ейлера

Обчислюємо крок інтегрування диференціального рівняння

- координати точок поділу відрізка інтегрування [x0,xk]

- метод Ейлера

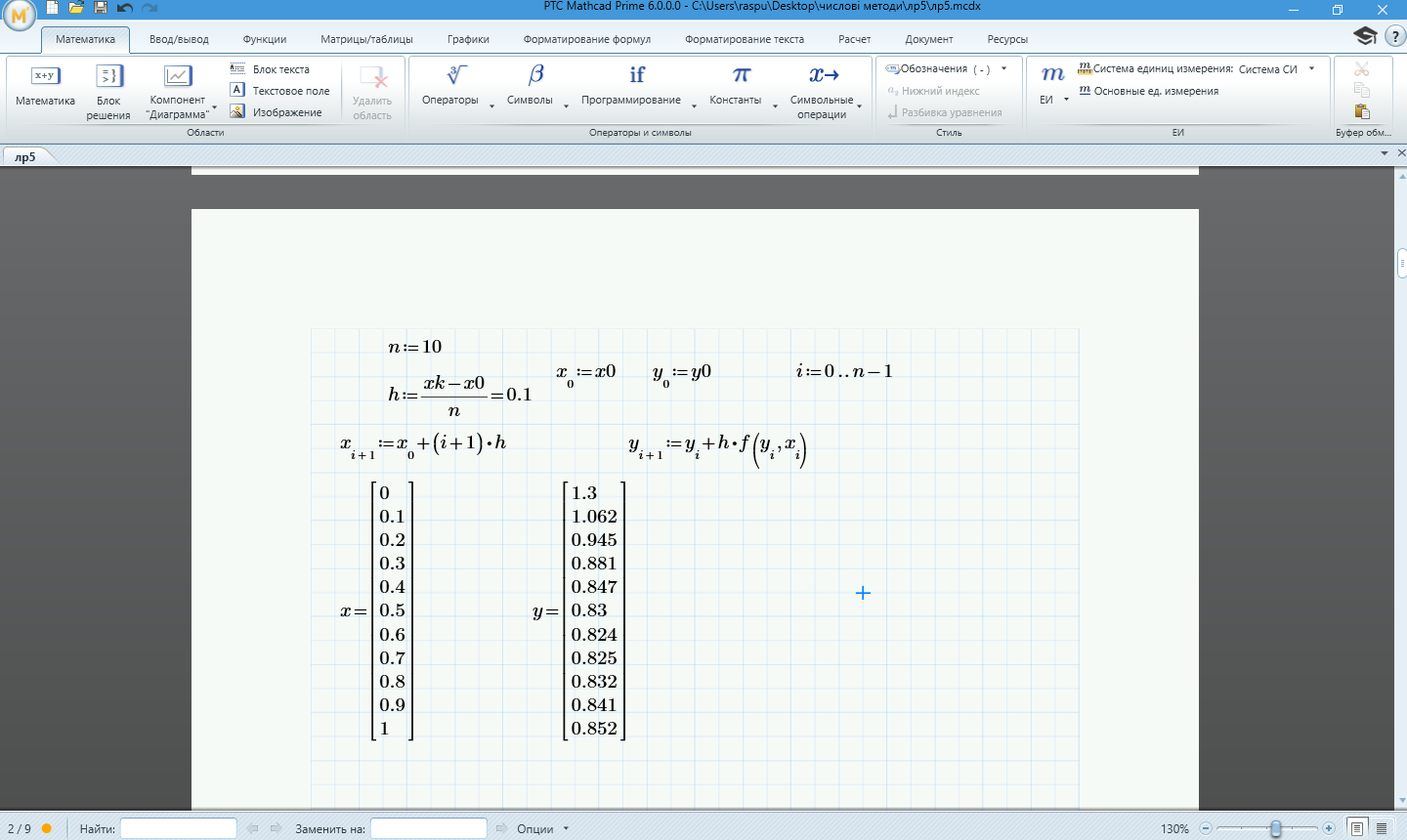
Рисунок 1.3 – Обчислення наближеного розв'язку диференціального рівняння методом Ейлера за допомогою програмного забезпечення MathCad

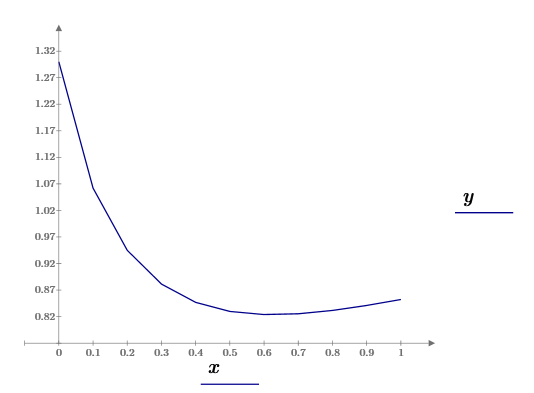
Рисунок 1.4 – Графік наближеного розв'язку диференціального рівняння методом Ейлера за допомогою програмного забезпечення MathCad

Метод Рунге-Кутта

- кількість елементарних відрізків, на які ділиться інтервал інтегрування [x0,xk]

Обчислюємо крок інтегрування диференціального рівняння

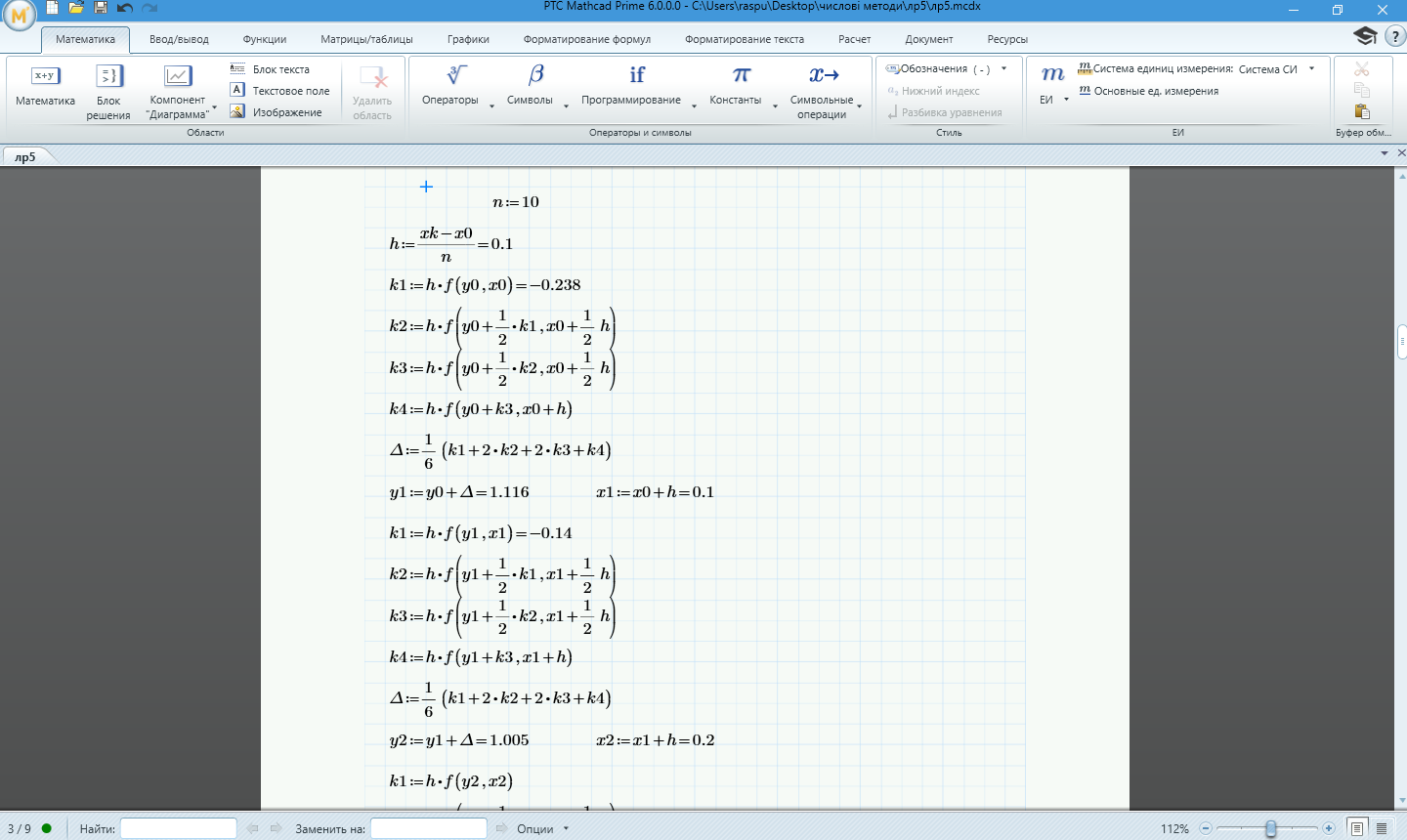Рисунок 1.5 – Обчислення наближеного розв'язку диференціального рівняння методом Рунге-Кутта за допомогою програмного забезпечення MathCad

Знайти наближений розв'язок систем звичайних диференціальних рівнянь

Спочатку знайдемо "точний" розв'язок системи

Для цього сформуємо наступні вектори

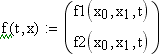- вектор-функція правих частин системи диференціальних рівнянь

- вектор початкових умов

- метод Рунге-Кутта з фіксованим кроком

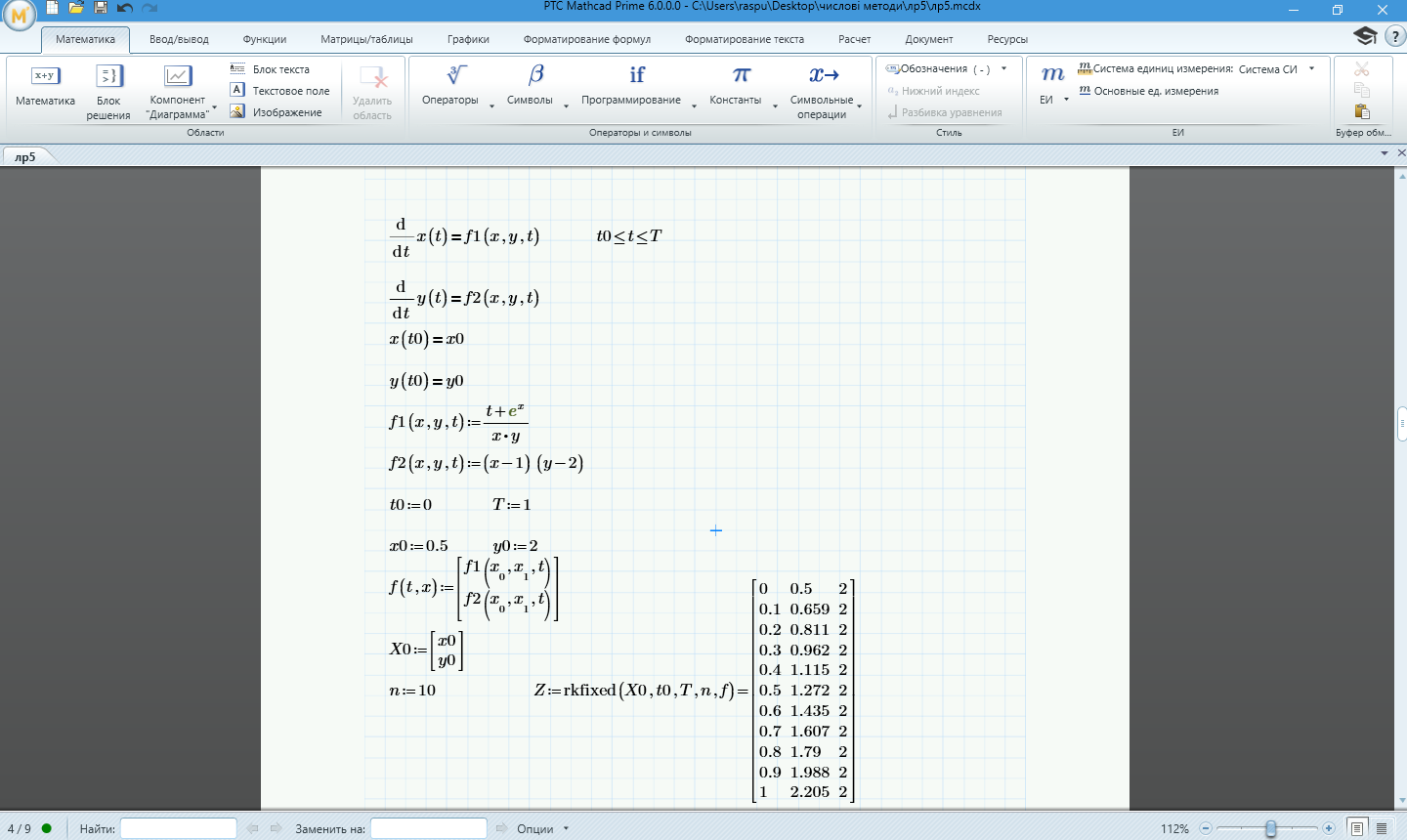
Рисунок 1.6 – Обчислення "точного" розв'язку системи диференціальних рівнянь за стандартних функцій системи MathCad

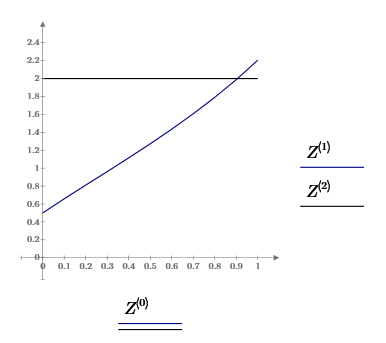
Рисунок 1.7 – Графік "точного" розв'язку системи диференціальних рівнянь за стандартних функцій системи MathCad

Метод Ейлера

Рисунок 1.8 – Обчислення наближеного розв'язку системи диференціальних рівнянь методом Ейлера за допомогою програмного забезпечення MathCad

Рисунок 1.9 – Графік наближеного розв'язку системи диференціальних рівнянь методом Ейлера за допомогою програмного забезпечення MathCad

Метод Рунге-Кутта

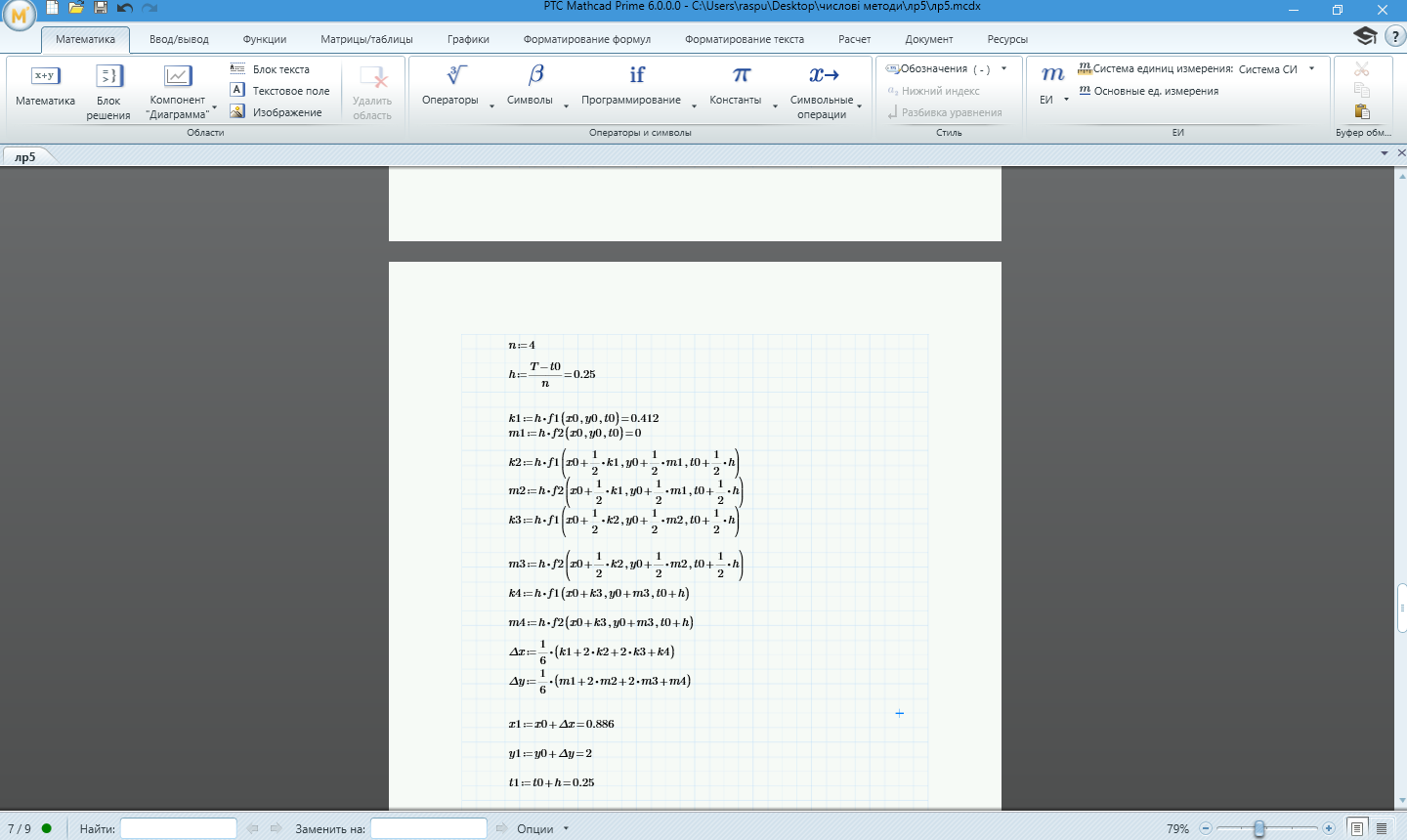
Рисунок 1.10 – Обчислення наближеного розв'язку диференціального рівняння методом Рунге-Кутта за допомогою програмного забезпечення MathCad

Програми

Метод простої ітерації

#include <math.h>

#include <iostream>

using namespace std;

double eps=2.718;

double f(double x, double y)

{

return (1+0.8*y*sin(x)-2*y*y);

}

double f1(double x,double y,double t)

{

return ((t+pow(eps,x))/(x*y));

}

double f2(double x,double y,double t)

{

return ((x-1)*(y-2));

}

int main()

{

system("chcp 1251");

system("cls");

int n=10;

int i;

int k=1;

float x=0;

float y=1.3;

cout << "Введіть n: ";

cin>>n;

float h=(k-x)/n;

cout << "\tРозрахунок методом Ейлера\n";

for(int i=0; i<n; ++i)

{

y=y+h*f(x,y);

x=x+h;

cout <<i+1<< ") Значення х: " << x;

cout.precision(4);

cout << "\tЗначення у: " <<y <<endl;

}

x=0;

y=1.3;

h=(k-x)/n;

cout << "\tРозрахунок методом Рунгe-Кутта:\n";

float k1,k2,k3,k4,dy;

for (i=1; i<n; i++)

{

k1=h*f(x, y);

k2=h*f((x+(h*0.5)),(y+(0.5*k1)));

k3=h*f((x+(h*0.5)),(y+(0.5*k2)));

k4=h*f((x+h), (y+k3));

dy=(k1+2*k2+2*k3+k4)/6;

y=y+dy;

x=x+h;

cout <<i<< ") Значення х: " << x<< "\tЗначення у: " <<y <<endl;

}

cout<<endl << " Розрахунок диференціальних рівнянь методом Ейлера:\n";

double t=0,x0=0.5,y0=2,T=1;

h=(T-t)/n;

for(int i=0; i<n; i++)

{

x=x0;

y=y0;

x0=x0+h*f1(x,y,t);

y0=y+h*f2(x,y,t);

t+=h;

cout <<i+1<< ") Значення х: " << x0 << "\tЗначення у: " <<y0 <<"\tЗначення t: "<<t<<endl;

}

cout<<endl << "Розрахунок диференціальних рівнянь методом Рунге-Кутта:\n";

double m1,m2, m3, m4, dx ;

t=0,x=0.5,y=2,T=1,dy=0;

h=(T-t)/n;

for (int i=0; i<n; i++)

{

k1=h*f1(x, y, t);

k2=h*f1((x+(0.5*k1)),(y+(0.5*m1)),(t+(0.5*h)));

m2=h*f2((x+(0.5*k1)),(y+(0.5*m1)),(t+(0.5*h)));

k3=h*f1((x+(0.5*k2)),(y+(0.5*m2)),(t+(0.5*h)));

m3=h*f2((x+(0.5*k2)),(y+(0.5*m2)),(t+(0.5*h)));

k4=h*f1((x+k3),(y+m3),(t+h));

m4=h*f2((x+k3),(y+m3),(t+h));

dx=(k1+2*k2+2*k3+k4)/6;

dy=(m1+2*m2+2*m3+m4)/6;

x=x+dx;

y=y+dy;

t+=h;

cout <<i+1<< ") Значення х: " << x << "\tЗначення у: " <<y<< "\tЗначення t: " <<t <<endl;

}

return 0;

}

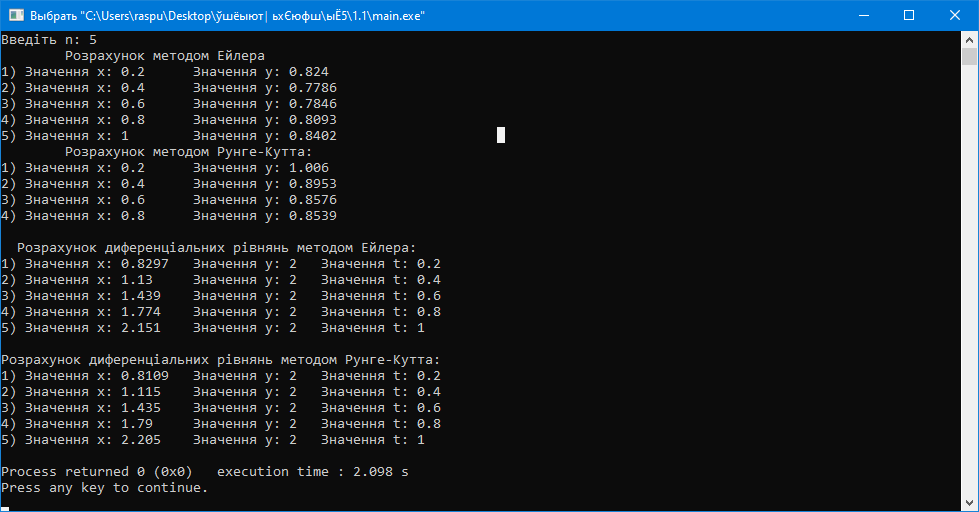
Рисунок 1.11 – Результат виконання програми

Висновок: на даній лабораторній роботі було обчислено звичайні диференціальні рівняння та їх системи за допомогою методів Ейлера, Рунге-Кутта, останній є більш точним.