
Book_2016_Liubchyk_Vyshcha_matemat_teoriia_funkts
.pdf
Подамо вираз 2t 1 аргумента t у вигляді виразів аргументів
t 2 і t 3 , відповідно: |
|
2t 1 2 t 2 2 1 2 t 2 5 , |
(3.38) |
2t 1 2 t 3 3 1 2 t 3 7 . |
(3.39) |
Враховуючи записи (3.38) і (3.39), отримаємо новий вираз для функції f t :
f t 2 t 2 t 2 5 t 2 2 t 3 t 3 7 t 3 . (3.40)
Оскільки
t p12 ; 1 1p ,
то, за теоремою про запізнення оригінала (3.27), остаточно маємо:
F p |
2 |
e 2 p 5 |
1 |
e 2 p 2 |
1 |
e 3 p 7 |
1 |
e 3 p |
|
2 5 p |
e 2 p |
2 7 p |
e 3 p . |
||
p2 |
|
p2 |
|
|
|
||||||||||
|
|
p |
|
|
|
p |
|
p2 |
|
p2 |
|||||
П р и к л а д 3.19. |
За даним |
графіком |
оригінала |
знайти зобра- |
|||||||||||
ження.
f t
1
0 a |
2a 3a 4a |
t |
Рисунок 3.5
Р о з в ’ я за н н я .
Подамо функцію, зображену на графіку (рис.3.5) аналітично:
135

при 0 t a |
f1 t 1 , |
|
|
|
|
|
|
||||||||||||
при a t 2a |
|
f2 t 0 . |
|
|
|
|
|
|
|||||||||||
При 2a t 3a функцію зображено відрізком прямої, яка прохо- |
|||||||||||||||||||
дить через точки M1 2a;0 |
і |
M2 3a;1 . Рівняння прямої, яка прохо- |
|||||||||||||||||
дить через точки M1 і M2 , має вигляд: |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
t t1 |
|
f t f t1 |
. |
(3.41) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
t2 t1 |
|
f t2 f t1 |
|
|||||
В точках M1 і M2 , враховуючи (3.41), маємо: |
|
||||||||||||||||||
|
t 2a |
|
|
f t 0 |
; |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
3a 2a |
|
1 0 |
|
|
|
|
|
|
||||||||||
|
t 2a |
f t . |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Отже, при 2a t 3a : |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
f3 t |
1 |
t 2a . |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
||
При 3a t 4a функцію зображено відрізком прямої, яка прохо- |
|||||||||||||||||||
дить через точки M2 3a;1 |
і |
M3 4a;0 . За формулою (3.41) складемо |
|||||||||||||||||
рівняння прямої M 2 M3 : |
|
|
|
|
|
|
|||||||||||||
|
t 3a |
|
|
f t 1 |
, |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
4a 3a |
|
0 1 |
|
|
|
|
|
|
||||||||||
|
t 3a |
|
f t 1 |
, |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
a |
|
1 |
|
|
|
|
|
|
||||||||||
f t 1 t 3a . a
136
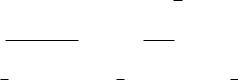
|
Таким чином, при |
3a t 4a |
функція-оригінал має |
вигляд: |
|||||||||||||||
f4 |
t 1 |
t 3a |
|
|
4a t |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
a |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
При t 4a : |
f5 t 0 . |
|
|
|
|
|
|
|
|
|||||||||
|
Остаточно отримаємо аналітичні вирази для оригінала: |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
0, |
t 0; |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
1, |
0 t a; |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
0, |
a t 2a; |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
f t |
|
1 |
|
t 2a , 2a t 3a; |
|
|||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
4a t |
, 3a t 4a; |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
a |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
0, |
t 4a. |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Запишемо оригінал |
f t |
одним аналітичним виразом за зразком |
||||||||||||||||
(3.36): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f t t t a |
|
t 2a |
t 2a |
t 2a |
t 3a |
|
||||||||||||
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
a |
|
|||||
|
|
|
|
4a t |
t 3a |
|
4a t |
t 4a . |
(3.42) |
||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
a |
|
|
|
|
|
|
|
a |
|
|
|
|
||
|
За теоремою запізнення (3.27) функція Хевісайда t |
є множ- |
|||||||||||||||||
ником, який говорить, що аргумент оригінала – це t . У відповідності з цим перетворимо оригінал (3.42):
ft t t a 1a t 2a t 2a
t 2a 4a t t 3a t 4a t 4a t t a a a
1a t 2a t 2a a2 t 3a t 3a 1a t 4a t 4a . (3.43)
137

Оскільки
t p12 ; 1 1p ,
то за теоремою запізнення остаточно отримаємо зображення для ори-
гінала (3.43):
F p |
1 |
|
1 |
e ap |
|
e 2ap |
|
|
2e 3ap |
|
e 4ap |
. |
|
|
|
|
ap2 |
|
ap2 |
|
|
||||||||
|
|
p |
p |
|
|
|
|
ap2 |
|
|||||
9°. Теорема множення (теорема про згортку ) . |
Згорт- |
|||||||||||||
кою двох оригіналів |
f1 t і |
f2 t , яка позначається f1 t f2 |
t , нази- |
|||||||||||
t |
f2 t d : |
|
|
|
|
|
|
|
||||||
вається інтеграл f1 |
|
|
|
|
|
|
|
|||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
f1 t f2 t f1 |
f2 |
t d . |
(3.44) |
|||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
Якщо виконати заміну у виразі (3.44), то не важко показати, що:
|
t |
t |
|
|
|
|
f1 |
f2 t d f1 t f2 |
d . |
(3.45) |
|
|
0 |
0 |
|
|
|
Тео рема 3.10. |
Нехай оригінали f1 t |
і f2 |
t |
мають зображен- |
|
ня F1 p і |
F2 p , |
відповідно: f1 t F1 p |
і |
f2 t F2 p . |
|
Тоді згортка (3.44) має своїм зображенням добуток відповідних зображень F1 p F2 p :
f1 t f2 t F1 p F2 p .
П р и к л а д 3.20. Знайти згортку двох оригіналів f |
t t2 |
і |
1 |
|
|
f2 t e2t та її зображення. |
|
|
138

Р о з в ’ я за н н я .
Знайти згортку двох оригіналів |
|
f t |
t2 |
і f |
2 |
t e2t |
та її зобра- |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ження. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Скористаємося |
означення |
м згортки (3.44): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
t 2 e2t |
t 2 e2 d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
udv uv vdu формула інтегрування частинами |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
u t 2 du 2 t d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
dv e2 d v e2 d |
1 |
e2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
t 2 |
t |
1 |
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
u t du d |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
e2 |
|
|
|
|
2 |
|
|
t |
e2 d |
dv e d v |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
2 |
|
2 |
|
0 |
|
|
e |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
t e2 |
0 |
|
1 e2 d t |
|
t |
1 1 e2 |
|
0 |
t |
|
|
t |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
t |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
t |
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
2 |
0 |
|
|
|
2 |
2 |
2 |
|
2 |
|
|
|
2 |
|
|
2 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
e |
2t |
|
1 |
|
|
1 |
e |
2t |
|
|
1 |
2t |
2 |
2t 1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
4 |
|
|
4 |
|
4 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
За теоремою 3.10 знайдемо зображення для згортки t2 e2t :
t2 p2!3 ;
П р и к л а д 3.21.
e2t |
1 |
t 2 e2t |
2 |
. |
|
p 2 |
p3 p 2 |
||||
|
|
|
Знайти зображення оригінала
t
t cos t e2 d .
0
|
Р о з в ’ я за н н я . |
|||||
|
|
|
|
|
||
|
Оригінал, |
|
|
з |
означення |
(3.44), є згорткою двох оригіналів |
f |
t cos t і |
f |
2 |
t e2t . |
||
1 |
|
|
|
|
|
|
139

Оскільки |
|
|
|
|
|
|
|
|
|
f |
t cos t |
p |
; |
f |
|
t e2t |
1 |
, |
|
|
|
|
|
||||||
p2 1 |
|
p 2 |
|||||||
1 |
|
|
|
2 |
|
|
|||
то за теоремою 3.10 (теорема множення ), маємо:
cos t e2t |
p |
|
|
1 |
. |
p2 1 |
|
||||
|
|
p 2 |
|||
Остаточно отримаємо:
t |
|
|
|
p |
|
|
cos t e2 d |
|
|
|
|
. |
|
|
|
|
|
|
||
|
p |
2 |
|
|
||
0 |
|
|
||||
|
|
|
1 |
p 1 |
|
140

§4. Знаход же ння оригі н ала за дан им зоб ра ження м
Розглянемо задачу, обернену до попередніх: знайти оригінал за існуючим зображенням.
В загальному випадку можна скласти таблицю зображень багатьох функцій і за нею визначати оригінал для даного зображення. В теорії інтегральних перетворень існує формула оберненого перетворення, яка за даним зображенням дозволяє знаходити оригінал:
f t |
1 |
s i |
F p e pt dp . |
|
|
|
(4.1) |
||||
2 i |
|||||
|
s i |
|
|
||
|
|
|
|
Однак, в більшості випадків, означення оригінала за даним зображенням можна провести значно простіше. Це пов’язано з тим, що більшість зображень мають вигляд раціональних дробів. Тому обернене перетворення може бути зведено до наступних теорем.
Тео рема 4.1 (1-а теорема розкладання ). Якщо зображен-
|
|
|
|
|
|
k |
an |
|
||
ня F p |
може бути подано у вигляді суми |
F p |
|
|
, де |
an |
||||
p |
n 1 |
|||||||||
|
|
|
|
|
|
n 0 |
|
|
|
|
n |
|
|
|
|
|
|||||
0, k |
– деякі сталі, то відповідний цьому зображенню оригінал має |
|||||||||
вигляд: |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
f t |
an |
t n . |
|
|
(4.2) |
||
|
|
|
|
|
|
|||||
|
|
|
n 0 n! |
|
|
|
|
|
||
Тео рема 4.1 (2-а теорема розкладання ). Якщо зображен-
ня є правильним раціональним дробом: F p R p , то, розкладаючи
Q p
її на найпростіші дроби, отримаємо суму зображень для найпростіших оригіналів.
П р и к л а д 4.1. Знайти оригінал за даним зображенням
F p |
4 p 5 |
|
|
. |
|
p 2 p2 4 p 5 |
||
141
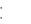
Р о з в ’ я за н н я .
Розкладемо початкову функцію F p на суму простих дробів:
|
|
|
|
|
4 p 5 |
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
Bp C |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
p 2 p2 4 p 5 |
p 2 |
p2 4 p 5 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
A p2 4 p 5 Bp C p 2 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
p 2 p2 4 p 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
4 p 5 A p2 4 p 5 Bp C p 2 , |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
p 2 8 5 A 4 8 5 17 A 13 A |
|
13 |
. |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
17 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
p2 |
|
A B 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
p0 |
5A 2C 5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
B A B |
13 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
5A 5 |
|
|
|
|
|
|
5 |
|
13 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
4 |
|
|
|
10 |
|
|
|
|
|
|
|
|||||||||||||
C |
|
|
C |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
||||||||||||||||
2 |
|
2 |
17 |
|
2 |
|
|
|
|
|
17 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Знаходячи коефіцієнти A , |
B і C , отримаємо: |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
F p |
13 |
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
13 p 10 |
. |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17 p |
|
17 |
|
|
p2 4 p 5 |
||||||||||||||||||||||||||||
Для дробу |
|
|
1 |
|
|
маємо оригінал e2t : |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
p |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
e2t . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Перетворимо другий дріб: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
13 p 10 |
|
|
13 p 2 2 10 |
13 p 2 13 2 10 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
p2 4 p |
5 |
|
|
|
|
p 2 2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p 2 2 1 |
|
||||||||||||||||||||||||||||
|
13 p 2 16 |
13 |
|
|
p 2 |
|
|
|
|
16 |
|
|
|
|
1 |
|
|
|
|
. |
|
|
|
|||||||||||||||||||||||||||||
|
p 2 2 1 |
p |
2 2 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
p 2 2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||||||||||||||||||||||||||||||
142
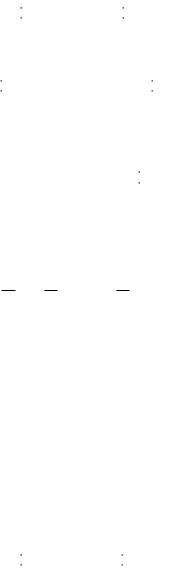
Оскільки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
cos t ; |
|
sin t , |
|
||||||||||
|
|
|
|
|
|
|
|
|
p2 1 |
p2 1 |
|
||||||||||||||
то за теоремою зсунення (3.24) маємо: |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
p 2 |
|
e 2t cos t ; |
1 |
|
e 2t |
sin t . |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
p 2 2 1 |
|
|
|
|
|
|
p 2 2 |
1 |
|
|
|
|||||||||
Використовуючи властивість лінійності, знайдемо оригінали для |
|||||||||||||||||||||||||
кожного з доданків: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
13 |
|
|
1 |
|
13 |
|
|
|
p 2 |
|
|
16 |
|
|
1 |
|
|
13 |
e2t |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
17 p 2 2 |
|
|
||||||||||||
17 p 2 |
17 p 2 2 |
1 |
1 |
17 |
|
|
|||||||||||||||||||
|
|
13 |
e 2t cos t |
16 |
e 2t sin t . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
17 |
|
|
|
|
|
17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Таким чином, оригіналом даного зображення є функція:
ft 1713 e2t 1713 e 2t cos t 1716 e 2t sin t .
Пр и к л а д 4.2. Знайти оригінал за даним зображенням
F p |
|
|
p |
|
. |
|
|
|
|
||
|
p2 |
|
2 |
||
|
|
|
|||
|
|
1 |
|
|
Р о з в ’ я за н н я .
У даному випадку подамо F p у вигляді добутку двох простих дробів:
|
|
|
p |
|
|
|
1 |
|
|
|
p |
||
|
|
|
|
|
|
|
|
|
|
|
. |
||
|
|
|
|
2 |
|
2 |
|
|
|
2 |
|||
|
|
|
|
p |
|
1 |
|
p |
1 |
||||
|
p |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Скористаємося теоремою про згортку. Оскільки
1 |
|
sin t ; |
p |
cos t , |
|
|
|
|
|
||
p2 1 |
p2 1 |
||||
143

то за формулою (3.46)
1 |
|
|
p |
sin t cos t . |
|
|
|
|
|
||
p2 1 |
p2 1 |
||||
Знайдемо згортку sin t cos t . З означення (3.44) маємо:
t
sin t cos t sin cos t d
0
|
t |
1 |
sin |
t |
|
sin |
|
|
t |
|
|
|
|
||||||||
|
2 |
|
|
|
|
|
||||
|
0 |
|
|
|
|
|
|
|
|
|
|
1 |
|
t |
sin t sin 2 t d sin t |
||||||
|
|
|
||||||||
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
0 |
|
|
|
|
|
|
|
|
d |
|
||
|
|
|
|
t |
1 |
t |
|
d |
sin 2 t d |
||
2 |
|||
0 |
0 |
||
|
|||
|
|
2 t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin t |
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|||||
|
d 2 t 2d |
|
|
|
|
t0 |
|
|
|
|
|
sin 2 t d 2 t |
||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
2 |
|||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
||||||||||||||
|
|
d |
d 2 t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
t sin t |
|
|
|
1 |
|
cos 2 t |
|
t0 |
|
t sin t |
|
1 |
|
cos t cos t |
|||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
2 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
4 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
t cos t |
|
|
1 |
cos t cos t |
t cos t |
. |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
2 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||
Остаточно отримаємо: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
t cos t |
. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
144
