3. Випадкові величини

3.1 Дискретні випадкові величини

Випадковою величиною називається величина, що у результаті експерименту приймає значення до його проведення невідоме. Випадкова величина, будучи функцією елементарних подій, позначається прописними літерами латинського алфавіту (X, Y, Z, …), а значення, що вона приймає, - малими літерами (x, y, z, …).

Дискретна випадкова величина – це величина, що у результаті проведення експериментів приймає кінцеву або рахункову безліч значень (яку можна пронумерувати).

Рядом розподілу дискретної випадкової величини називається таблиця всіх значень випадкової величини з відповідними значеннями імовірності :

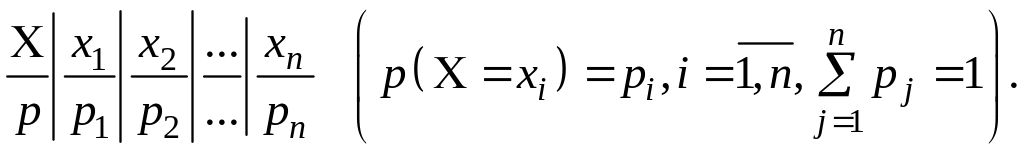
Функцією розподілу дискретної випадкової величини називається функцією (це функція стрибків), рівна імовірності того, що в результаті експерименту випадкова величина прийме значення менше :

де підсумовування ведеться за всіма значеннями для яких .

Імовірність улучення значення випадкової величини в інтервал визначається формулою

Густиною розподілу дискретної випадкової величини називається узагальнена похідна функції розподілу, обумовлена формулою

де дельта-функція.

Математичним сподіванням або середнім значенням дискретної випадкової величини називається число, що дорівнює сумі всіх значень випадкової величини, помножених на відповідні їм імовірності:

Властивості математичного сподівання:

1) лінійність, де с₁ і с₂ – константи;

2) -, якщо C₁ і C₂ – незалежні випадкові величини.

Дисперсією випадкової величини C називається число, рівне математичному сподіванню квадрата відхилення C від m_x:

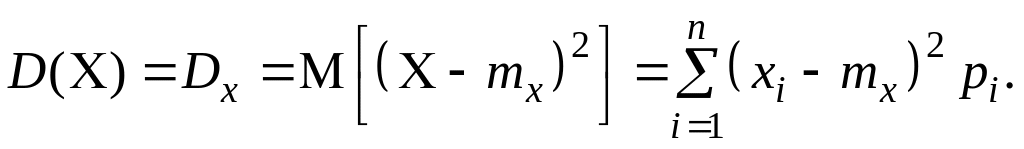
Дисперсія характеризує ступінь розкиду значень випадкової величини навколо математичного сподівання. Часто для обчислення дисперсії використовується формула

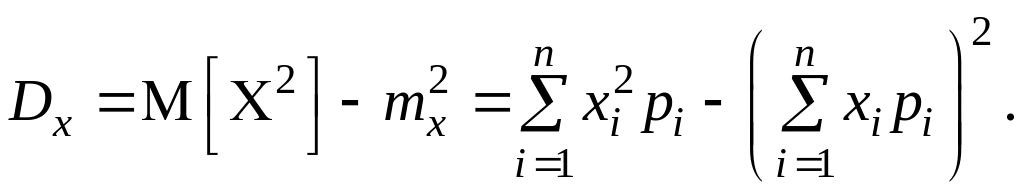
Середнім квадратичним відхиленням випадкової величини C називається число, що дорівнює кореневі квадратному з дисперсії:

3.1.1 Приклади розв’язання задач

3.1 П'ять конденсаторів випробуються при перевантажувальних режимах. Іспити незалежні й імовірність для кожного виробу їх пройти дорівнює 0,8. Іспити закінчуються після першого ж конденсатора, що не витримало іспиту. Знайти ряд розподілу числа іспитів.

Розв’язок. Позначимо через C число іспитів. Це випадкова величина, тому що до проведення дослідження невідомо, яке вона прийме значення. Нехай C = 1, тобто було проведено один іспит. Це значить, що при іспиті конденсатор вийшов з ладу й імовірність цієї події p = 1 – 0,8 = 0,2. Якщо було проведено рівно k іспитів (C = k, 1 < k < 5), то конденсатор успішно пройшов іспити, а k-й вийшов з ладу. Тому що іспити незалежні, то імовірність

Подія C = 5 означає, що чотири конденсатори витримали іспит, а результат п'ятого може бути будь який. Значить Таким чином, маємо наступну таблицю:

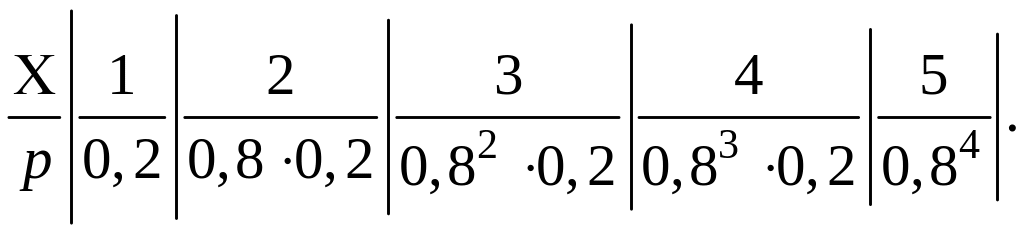
Перевіримо правильність отриманого ряду розподілу. Тому що в результаті проведення іспиту випадкова величина C обов'язково прийме одне з представлених у таблиці значень і події несумісні, то сума всіх імовірностей повинна дорівнювати одиниці. Дійсно,

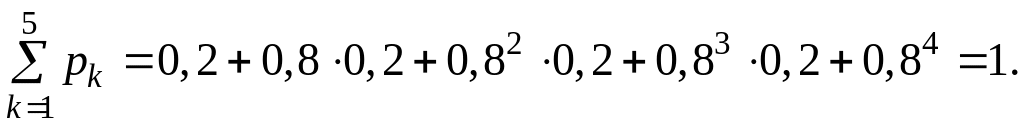
3.2. Проводиться три незалежних експерименти, у кожнім з яких подія А з'явиться з імовірністю 0,4. Випадкова величина Х - число появи події А в трьох експериментах.

1) Побудувати ряд розподілу випадкової величини Х.

2) Знайти функцію розподілу і побудувати її графік.

Розв’язок. Випадкова величина C може прийняти чотири значення: 0, 1, 2, 3. Знайдемо імовірність того, що випадкова величина C = 0. Це значить, що відбулася подія тобто в трьох експериментах не з'явилася подія А (А_i – поява події А в i-тім експерименті). Тому

Аналогічним способом знаходимо:

Ряд розподілу має вигляд:

Зробимо перевірку

2) Знайдемо функцію розподілу F(x). Якщо аргумент то випадкова величина C на інтервалі (-¥; 0) не прийме жодного значення. Значить імовірність цієї події дорівнює нулю:

У випадку випадкова величина C прийме лише одне значення C = 0, тому

Для випадкова величина C може прийняти значення 0 або 1. Отже,

Продовжуючи аналогічним образом, остаточно можна записати

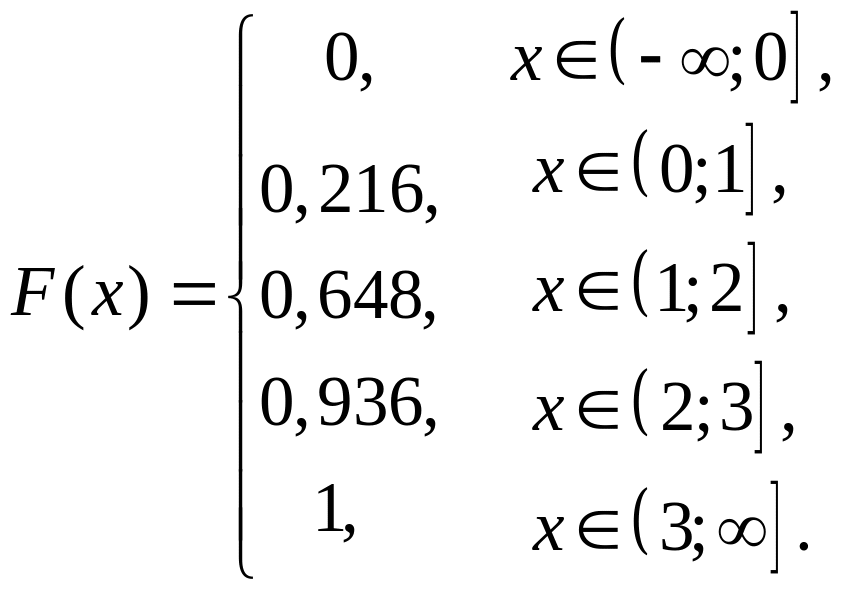
Графік функції розподілу має вигляд:

3.3 До джерела живлення на деякі проміжки часу в довільному сполученні можуть підключатися будь-які з трьох навантажень, кожне з яких розсіює потужність 15 Вт. При цьому кожна з них підключена до джерела лише на одну четверту частину всього часу його роботи і діє незалежно від інших.

1) Визначити середню потужність, споживану навантаженнями від джерела.

2) Визначити дисперсію потужності, споживаної навантаженнями від джерела, і середнє квадратичне відхилення.

3) Якщо джерело може забезпечити тільки 40 Вт, то яка імовірність його перевантаження?

Розв’язок. Позначимо через Х число навантажень, що підключаються. Випадкова величина Х може прийняти значення 0, 1, 2, 3. Тому що кожне навантаження підключається до джерела лише на одну четверту частину всього часу роботи, то імовірність її роботи дорівнює 1/4.

Для рішення поставлених задач побудуємо ряд розподілу випадкової величини C. Нехай C = 0, тобто не підключені одночасно всі три навантаження. Тому що імовірність не підключення кожного навантаження дорівнює 3/4, то імовірність, що не підключені три навантаження, дорівнює добуткові імовірності не підключення навантажень . При C = 1 можуть бути такі події. Підключено перше навантаження і не підключені друге і третє, або друге підключено, а не підключені перше і третє, або третє підключено, а не підключені перше і друге. Імовірність події C = 1 дорівнює сумі імовірності цих трьох подій:

Міркуючи подібним чином, маємо:

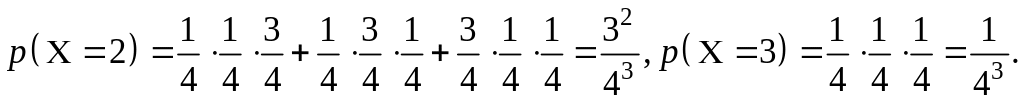
Таким чином, ряд розподілу випадкової величини C має вигляд:

Зробимо перевірку:

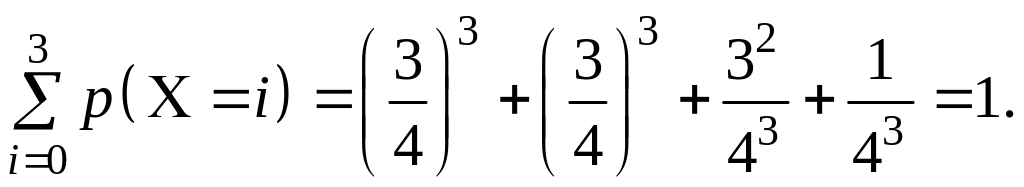
Уведемо тепер випадкову величину Y – величини потужностей навантажень, що підключаються. Події і - рівносильні, тому для випадкової величини Y маємо ряд розподілу:

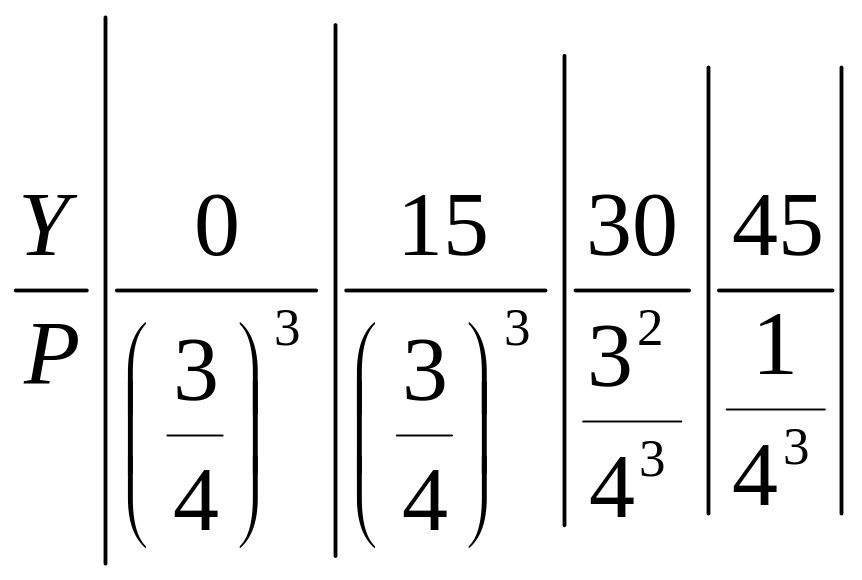
1)Середня потужність, споживана навантаженнями, дорівнює:

2)Дисперсію потужності, споживаної навантаженнями, будемо знаходити по формулі

Якщо випадкова величина Y прийме значення y₁ з імовірністю р₁, то випадкова величина Y² прийме значення з тією же імовірністю р₁. Тому ряд розподілу Y² буде відрізнятися від ряду випадкової величини Y тільки квадратами значень останньої. Значить

і

Середнє квадратичне відхилення дорівнює

3) Якщо джерело може забезпечити тільки 40 Вт, то імовірність його перевантаження є імовірність того, що випадкова величина Y прийме значення більше 40:

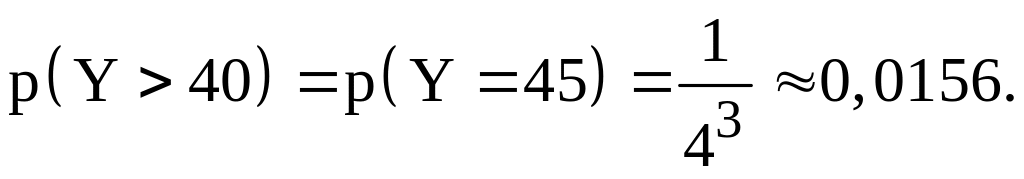
3.4. Два стрільці стріляють по одній мішені, роблячи незалежно один від одного по два постріли. Імовірність влучення в мішень для першого стрільця дорівнює 0,4, а для другого – 0,5. Нехай Х - число влучень у мішень першим стрільцем, а Y – число влучень у мішень другим стрільцем. Побудувати ряд розподілу випадкової величини Z = X – Y і знайти її математичне сподівання і дисперсію.

Розв’язок. Побудуємо ряд розподілу випадкових величин X і Y. Ці величини приймають значення 0, 1, 2, де 0, 1, 2 відповідно означають, що стрілець із двох пострілів промахнувся, влучив раз або влучив двічі в мішень. Нехай X = 0. Це значить, що перший стрілець обидва рази промахнувся. Імовірність цієї події

де A_i - подія, що складається з того, що перший стрілець i-тим пострілом влучив в мішень. Тому що , то . Подія Х = 1 складається з подій: перший стрілець першим пострілом влучив у мішень, а другим – ні, або навпаки. Тому

Нарешті

Запишемо ряд розподілу випадкової величини Х:

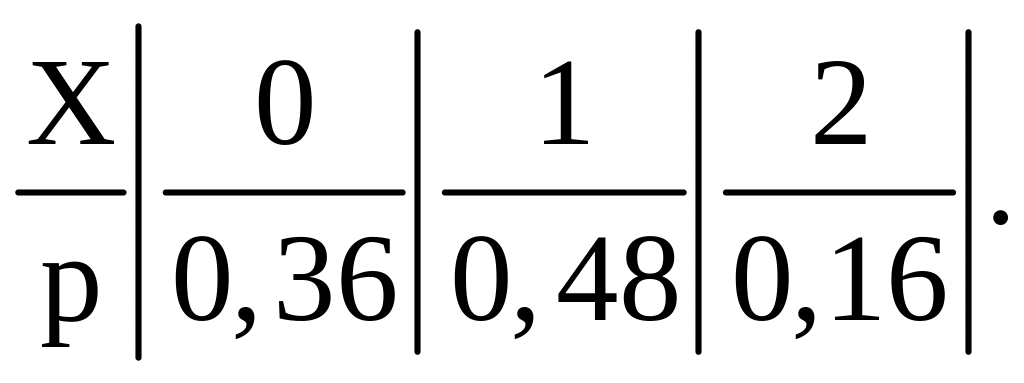
Аналогічним образом знаходимо ряд розподілу випадкової величини Y:

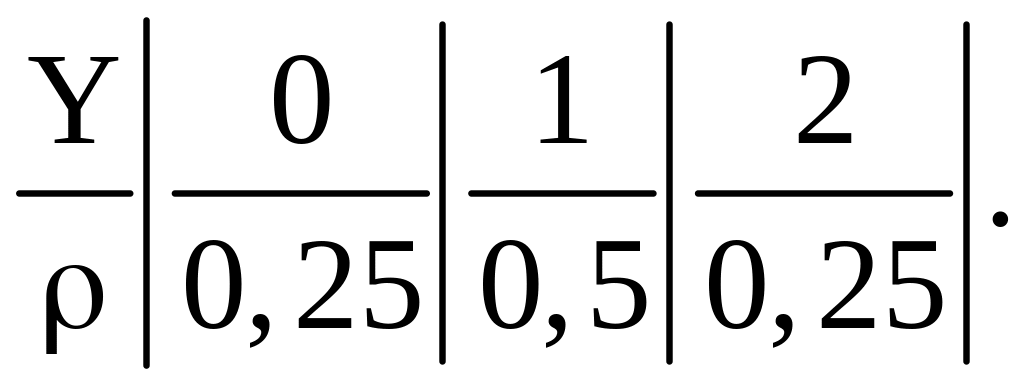
Випадкова величина Z = X - Y приймає значення –2, -1, 0, 1, 2. Значення Z = -2 вона прийме тільки тоді, коли Х = 0 і Y = 2. Тому

p (Z= -2) =p(X=0 и Y=2) =p(X=0) p(Y=2)=0,09.

Далі

p(Z=-1)=p(X=0 і Y=1 або X=1 і Y=2)=p(X=0)p(Y=1) + p(X=1)p(Y=2)=0,3,

p(Z=0)=p(X=0 і Y=0 або X=1 і Y=1, або X=2 і Y=2) =p(X=0)p(Y=0) + p(X=1)p(Y=1) +

+ p(X=2)p(Y=2)=0,37.

Аналогічним способом одержуємо

p(Z=1)=0,2, p(Z=2)=0,04.

Отже, маємо ряд розподілу Z:

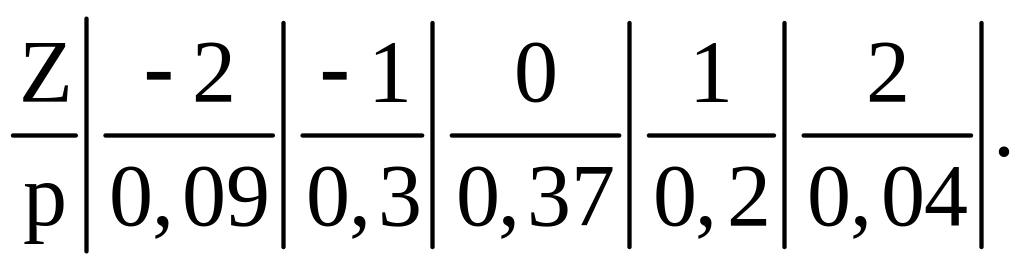
Використовуючи отриманий ряд розподілу, знайдемо числові характеристики випадкової величини Z: