
- •2.3.1 Приклади розв’язання задач ………………………………………… ……16
- •4.1.1 Приклади розв’язання задач ……………………………………… …… …57
- •1. Мета та завдання навчальної дисципліни
- •2.5 Рейтингове оцінювання успішності студентів
- •3. Начально-методичні матеріали
- •1. Загальні вказівки
- •2. Випадкові події
- •2.1 Приклади розв’язання задач
- •2. 2. Задачі
- •2.3.1 Приклади розв’язання задач
- •2.3.2 Задачі
- •3. Випадкові величини
- •3.1 Дискретні випадкові величини
- •3.1.1 Приклади розв’язання задач
- •3.1.2. Задачі
- •3.2. Безперервні випадкові величини
- •3.2.1. Приклади розв’язання задач
- •3.2.2. Задачі
- •3.3. Функція випадкової величини. Характеристичні функції
- •3.3.2 Задачі
- •4. Система випадкових величин
- •4.1.1. Приклади розв’язання задач
- •4.1.2. Задачі
- •4.2. Функціональне перетворення системи випадкових величин.
- •4.2.1 Приклади розв’язання задач
- •Розв’язок. Густина імовірності випадкової крапки (X,y,z) має вигляд
- •4.2.2 Задачі
- •5. Випадкові процеси
- •5.1. Приклади розв’язання задач
- •5.2 Задачі.
Розв’язок. Густина імовірності випадкової крапки (X,y,z) має вигляд

Три
координати прямокутної системи координат
у просторі (X,Y,Z) зв'язані зі сферичними
координатами
![]() співвідношеннями:
співвідношеннями:

Якобіан
перетворення від змінних x, y, z до змінних
![]()
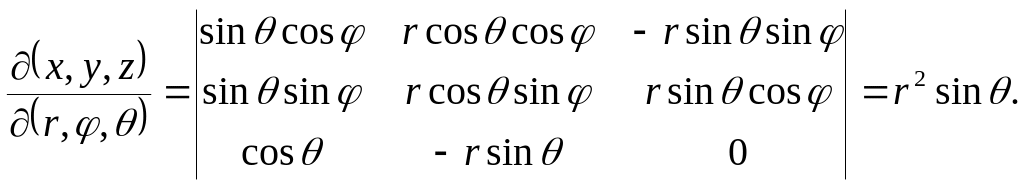
Таким
чином, густина імовірності в новій
системі
![]() матиме вигляд
матиме вигляд
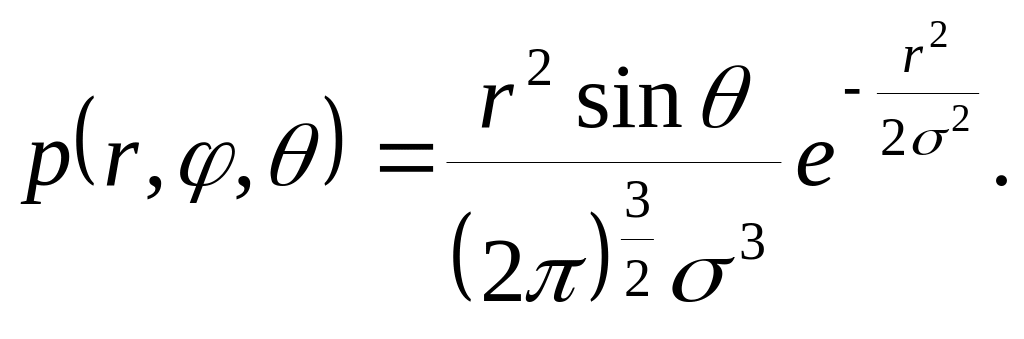
Значення випадкової величини розподілені на інтервалі , а випадкової величини θ - на інтервалі (0;π), тому шукана одновимірна густина імовірності
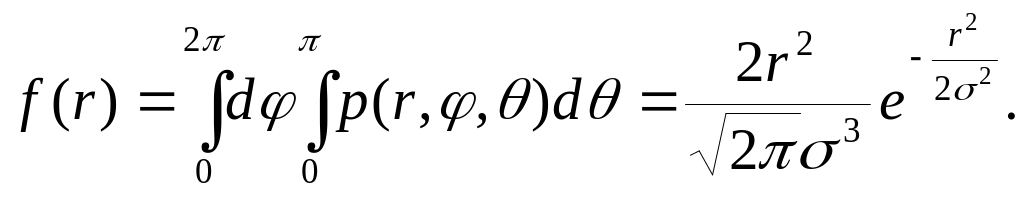
4.27. Знайти густину ймовірності двох незалежних випадкових величин (композицію законів) Z=X+Y, якщо Х – рівномірно розподілена у інтервалі [0;1], а випадкова величина Y має експоненційний розподіл
![]()
![]()
Розв’язок. Функції і не дорівнюють нулю тільки в окремих інтервалах. Графіки цих функцій мають вигляд (рис.3.13,3.14):

Рисунок 3.13 Рисунок 3.14
Тому спочатку зручно знайти функцію розподілу випадкової величини Z, а потім шляхом диференціювання цієї функції знайти густину імовірності величини Z.
За визначенням маємо
![]() ,
де Dz
– область, в середині якої x+y<z
і
жодна з функцій
,
не дорівнює нулю (рис.3.15.)
,
де Dz
– область, в середині якої x+y<z
і
жодна з функцій
,
не дорівнює нулю (рис.3.15.)
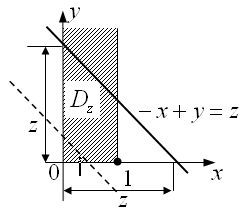
Рисунок 3.15
На
малюнку видно, що вигляд області
інтегрування буде різним залежно від
того, в якому з двох інтервалів (0;1) або
(1;![]() )
,буде знаходитись значення Z.
Проводячи розрахунки інтегралів для
цих випадків, одержуємо
)
,буде знаходитись значення Z.
Проводячи розрахунки інтегралів для
цих випадків, одержуємо
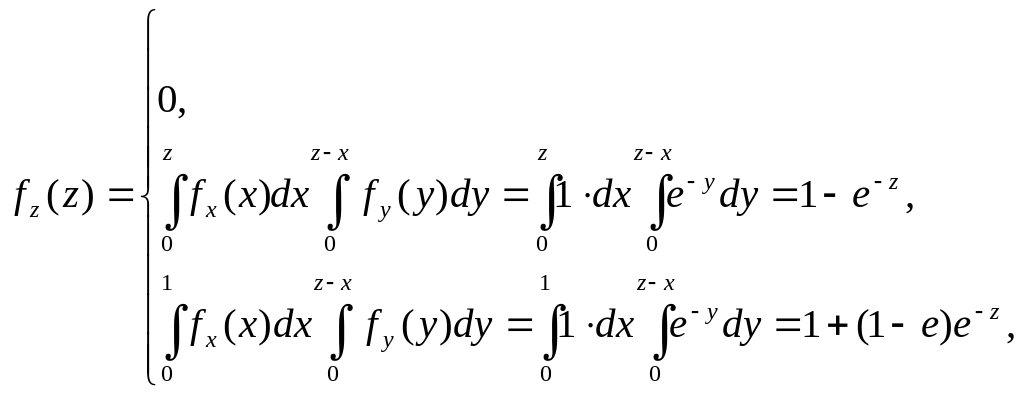
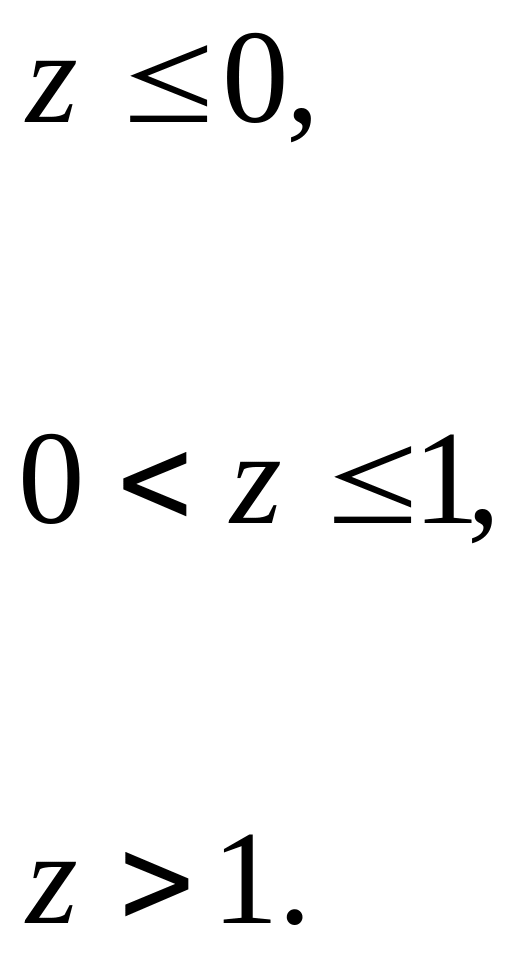
Взявши
похідну від функції
![]() ,
маємо густину імовірності випадкової
величини Z:
,
маємо густину імовірності випадкової
величини Z:
![]()
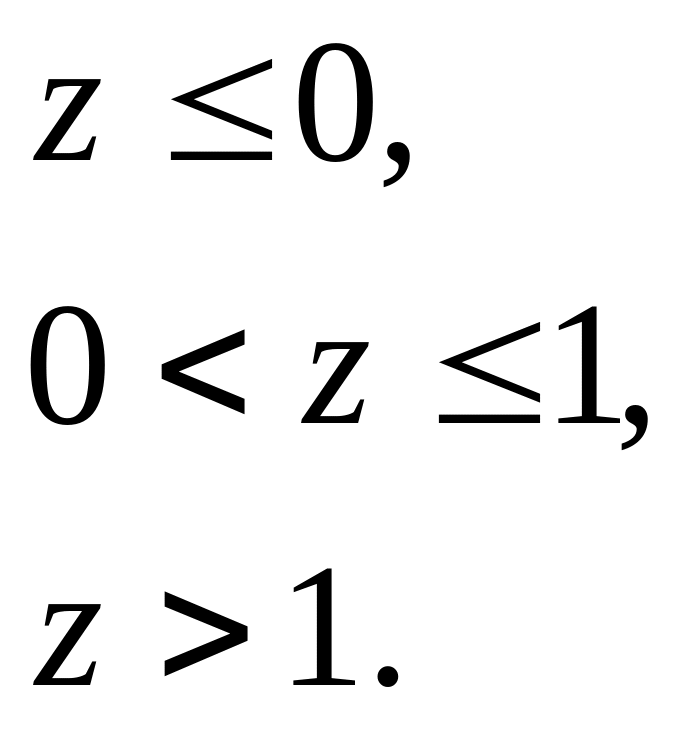
4.28. Два резистора з’єднані послідовно. Відомо, що опори резисторів є незалежними випадковими величинами X і Y, які рівномірно розподілені на інтервалі [R1,R2]. Знайти густину імовірності загального опору.
Розв’язок. Випадкова величина Z=X+Y. Через те, що густини ймовірностей і відповідно випадкових величин X та Y відрізняються від нуля тільки в окремих інтервалах, то, як і раніше, будемо знаходити функцію розподілу випадкової величини Z:
![]()
де
![]()

![]()
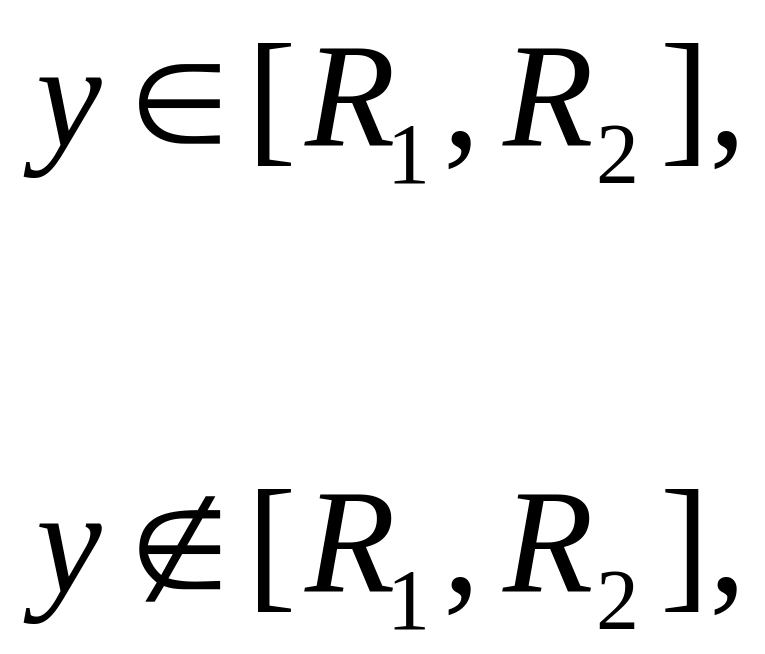
А Dz – область, яка зображена нижче (рис.3.16).
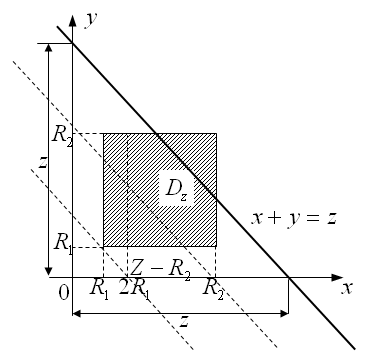
Рисунок 3.16
Розглянемо
чотири інтервали, в яких змінюється
величина Z:
![]() Тоді функція розподілу
Тоді функція розподілу


Отже, густина імовірності випадкової величини Z
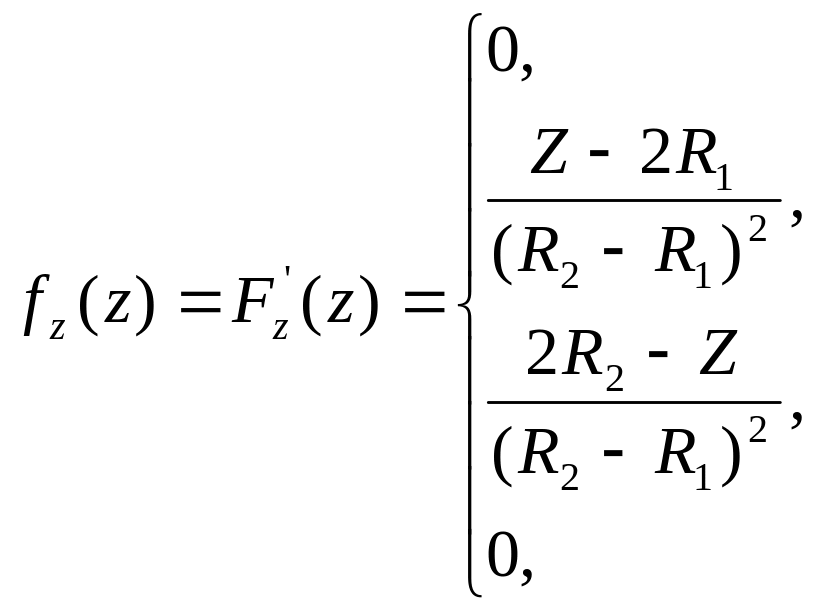

Графік густини імовірності випадкової величини Z має вигляд (рис.3.17)

Рисунок 3.17
4.29
Незалежні випадкові величини Х і У мають
нормальний закон розподілу відповідно
з параметрами
![]() ,
,
![]() і
і
![]() ,
,
![]() .
Знайти густину імовірності випадкової
величини Z=X+Y.
.
Знайти густину імовірності випадкової
величини Z=X+Y.
Розв’язок.
Густини ймовірностей
і
випадкових величин X i Y не приймають
нульові значення в жодній точці числової
осі, тому для знаходження композиції
законів застосовуємо апарат характеристичних
функцій. Спочатку знайдемо характеристичну
функцію нормованої нормально розподіленої
випадкової величини
![]() , густина імовірності якої
, густина імовірності якої
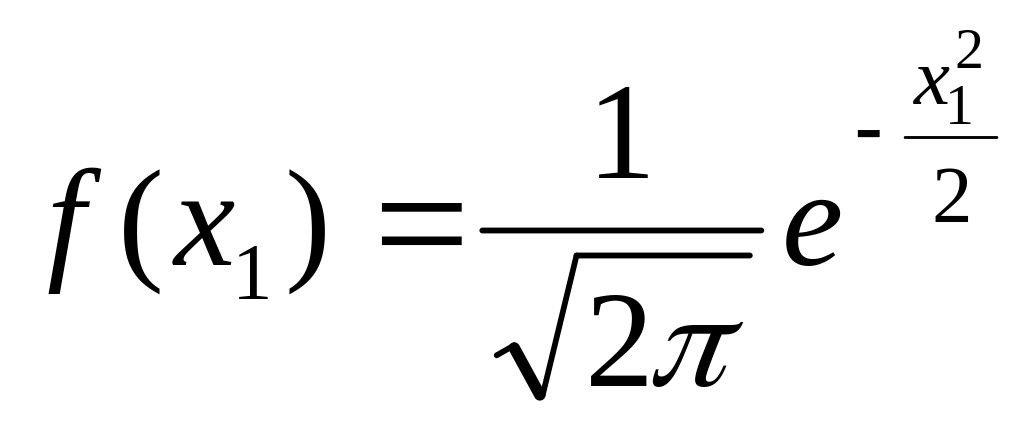 .
.
Відповідно до визначення характеристичної функції
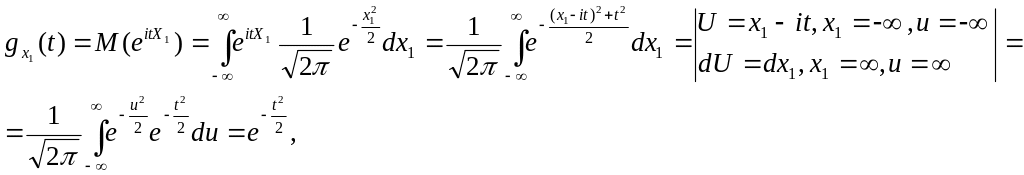
через те, що інтеграл Пуассона
![]() .
.
Зробимо лінійне перетворення
![]() .
.
Воно переводить нормовану нормальну величину у нормальну величину , параметри якої
![]()
![]() .
.
Знайдемо характеристичну функції випадкової величини :
![]()
Поміняв
![]() на
,
маємо і для випадкової величини
на
,
маємо і для випадкової величини
![]() характеристичну
функцію
характеристичну
функцію
![]()
Через те, що характеристична функція суми незалежних випадкових величин дорівнює добуткові характеристичних функцій, то
![]() ,
,
де
![]() ,
,
![]() . Звідси бачимо, що
. Звідси бачимо, що
![]() -
нормально розподілена випадкова величина
з параметрами
.
-
нормально розподілена випадкова величина
з параметрами
.
