5.1. Приклади розв’язання задач

5.1. Випадковий процес має вигляд

;

де А – випадкова величина, яка підпорядковується нормальному закону з параметрами ;

Знайти одновимірну густину імовірності , математичне сподівання , дисперсію та кореляційну функцію .

Розв’язок. Користуючись властивостями математичного сподівання та дисперсії, знаходимо:

Так як

,

То

При фіксованому (в перерізі) є нормально розподіленою випадковою величиною, характеристиками якої визначаються рівностями (3.2). Тому одновимірна густина імовірності має вид

5.2 Характеристики випадкового процесу задані наступними виразами

Знайти характеристики випадкового процесу

Розв’язок. Похідна є лінійне перетворення, тому

Для знаходження кореляційної функції визначимо центрований процес

Отже, кореляційна функція

а дисперсія

5.3. Знайти математичне сподівання і кореляційну функцію суми двох некорольованих випадкових процесів і з характеристиками:

Розв’язок. Математичне сподівання випадкового процесу :

Запишемо центрований процес y вигляді

Тоді кореляційна функція випадкового процесу

А так як процеси і -некорельовані, то

5.4. В результаті обробки осцилограми стаціонарного випадкового процесу типу нерегулярної качки з нульовим математичним сповіданіям одержано вираз для кореляційної функції

,

де D_х=50- дисперсія; - параметр затухання; - резонансна частота.

Знайти спектральну густину .

Розв’язок. Відповідно формули Вінера – Хінчіна спектральна густина

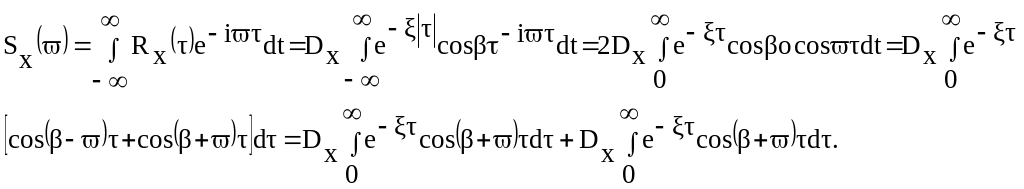Якщо кожний інтеграл два раза інтегрувати по частинам, то одержимо

.

Після підстановки числових значень параметрів маємо

5.5. Нехай випадковий процес задано аналітичним виразом вигляду

де - стаціонарний випадковий процес з кореляційною функцією

,

а - незалежна від процесу випадкова величина, рівномірно розподілена в інтервалі

Знайти кореляційну функцію випадково процесу та величину інтервалу його кореляції.

Розв’язок. За визначенням кореляційна функція випадкового процесу

Так як математичне сподівання процесу

тоді

Процес є стаціонарним з кореляційною функцією

Знайдемо

то він є і ергодичним.

За формулою

проводячи два раза інтегрування по частинам, знаходимо інтервал кореляції:

5.6. Стаціонарний процес з нульовим математичним сподіванням має спектральну густину

Знайти кореляційну функцію . Для випадку визначити найменшу величину при якому перерізи і некорельовані.

Розв’язок. За формулою Вінера – Хінчіна знаходимо

Для окремого випадку кореляційна функція набуває вигляду

Величину інтервалом можна визначити, прирівнявши до нуля одержану кореляційну функцію:

Звідси маємо, що перерізи випадкового процесу будуть некорельованими, якщо

Отже

де - верхня гранична частота спектральної густини S (ω). За заданою величиною Δt кількість некорельованих відліків N на інтервалі тривалістю T визначається, як N=T/Δt=2f₂T.

5.7 Випадковий процес X(t)=Asin(ωt+φ) є синусоїдою з випадковою фазою φ, яка рівномірно розподілена в інтервалі [-T;T]. Перевірити цей процес на ергодичність.

Розв’язок. Для перевірки на ергодичність заданого процесу X(t) слід обчислити середнє значення процесу і його кореляційну функцію Rx(t, t+τ) двома способами (шляхом усереднень за ансамблем реалізацій і за часом), а після цього отримані результати перевірити.

1) Усереднення за ансамблем (математичне сподівання):

(3.3)

З урахуванням того, що m_x(t)=0, обчислимо кореляційну функцію Rx(t, t+τ):

(3.4)

Із формул (3.3), (3.4) видно, що процес X(t) - стаціонарний.

2)Проведемо усереднення за часом. Візьмемо якусь реалізацію процесу X(t):

X (t)=Asin(ωt+φ)

і знайдемо усереднення її за часом

<X (t)>=

(3.5)

Усереднена за часом (часова) кореляційна функція

(3.6)

Із порівняння формул (3.3), (3.4) і (3.5), (3.6) видно, що знайдені значення не залежать від способу усереднення. Отже, аналізований процес можна вважати ергодичним.