4.1.1. Приклади розв’язання задач

4.1. Двовимірна густина розподілу випадкових величин X і Y дорівнює

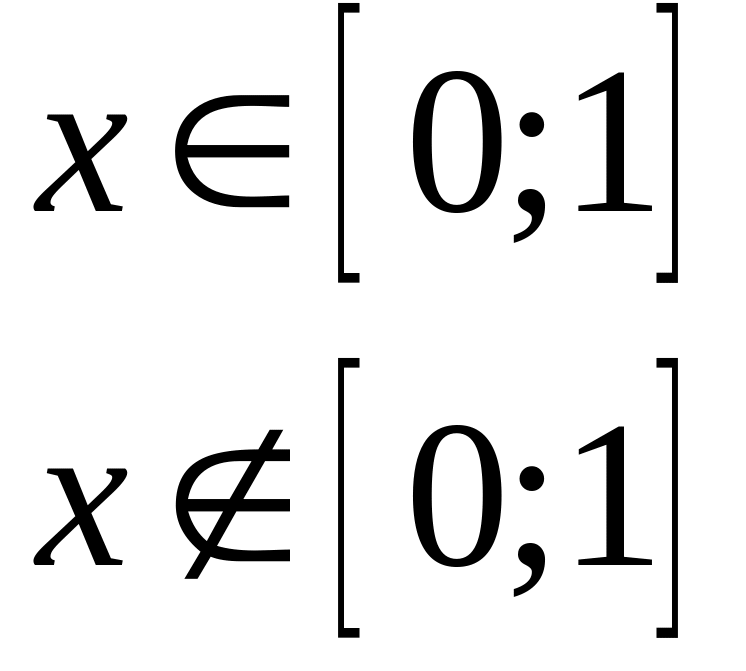
Знайти:

1) величину k;

2) імовірність події ;

3)одновимірну густину розподілу .

Розв’язок.

1) Величину k знаходимо з умови нормування густини розподілу:

2) Шукану імовірність знаходимо за формулою (3.1):

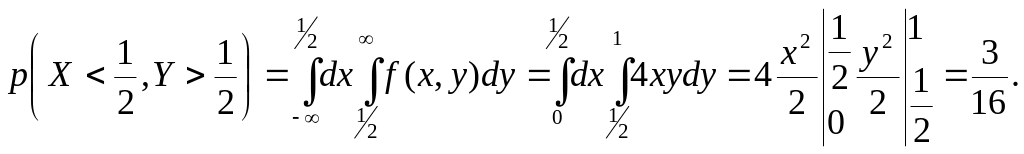
4) Одновимірна густина визначається через двовимірну густину за допомогою співвідношення

Підставимо вираз для густини в інтеграл:

Якщо то підінтегральна функція дорівнює нулю, а отже і =0. Таким чином

4.2. Система двох випадкових величин (X,Y) підпорядкована рівномірному закону розподілу в трикутнику, обмеженому прямими х=0, y=0, x+у=a (a>0). Визначити функцію розподілу системи випадкових величин (X,Y).

Розв’язок. Спочатку знайдемо густину розподілу системи Тому що за умовою система двох випадкових величин підпорядкована рівномірному закону розподілу в трикутнику, то

де С- константа, - область, обмежена трикутником. З умови нормування густини імовірності знаходимо константу C:

Отже

Функцію розподілу

будемо знаходити для координат (x,y) точок різних областей. Розглянемо області точок, які на рисунках не заштриховані.

1).Нехай або (рис.3.4) Для точок цієї області підінтегральна функція дорівнює нулю, тому

Рисунок 3.4

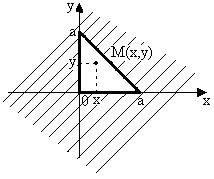
2).Для x>0, y>0, x+y (рис.3.5) маємо

=

Рисунок 3.5

3).Якщо (рис.3.6) то

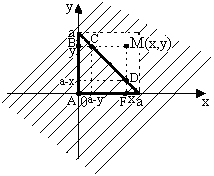
= = де - площі

відповідних фігур

4).Нехай (рис.3.7), тоді

Рисунок 3.6

=

=

=

Рисунок 3.7

5).Для (рис.3.8) маємо

=

=

Рисунок 3.8

6).Якщо (рис.3.9), то

Рисунок 3.9

4.3. Система двох випадкових величин рівномірно розподілена в трикутнику, обмеженому прямими Визначити середнє значення і дисперсію величини Х.

Розв’язок. Для знаходження характеристик випадкової величини Х (математичного сподівання і дисперсії) потрібно знати її густину імовірності яка визначається за густиною імовірності системи (X,Y) за допомогою формули

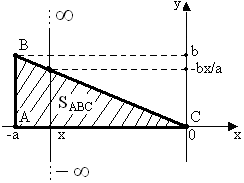
Через те що система (X,Y) підпорядкована рівномірному закону в трикутнику АВС (рис.3.10)

,

де С- константа, а - область, обмежена трикутником АВС. З умови

Рисунок 3.10

Отже

Тепер визначимо середнє значення величини Х:

Дисперсію знаходитимемо за формулою

А тому що

то

4.4. Нехай Х - дискретна випадкова величина, що набуває два значення х₁ і х₂ (х₂> х₁) з імовірностями p₁ і p_2.

Випадкова величина Y- неперервна величина; її умовним розподілом при служить нормальний закон з математичним сподіванням, рівним , і середнім квадратичним відхиленням, рівним

Знайти:

1)функцію розподілу системи (X,Y);

2)густину розподілу випадкової величини Y.

Розв’язок.

1)Функція розподілу

Нехай тоді і Якщо то і

При використовуючи формулу повної імовірності, маємо

Отже, для

Вважаючи і диференціюючи за змінною y, одержуємо

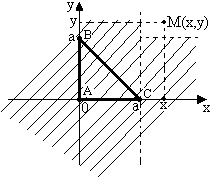
4 .5. Випадкова точка (X,Y) розподілена зі сталою густиною усередині заштрихованого квадрата R ( рис.3.11), знайти:

1) густину розподілу ;

2) густину розподілу випадкової величини Х і густину розподілу випадкової величини Y;

3)умовні густини розподілу і

Визначити:

4)залежні чи незалежні випадкові величини X, Y;

5)кореляційні вони чи ні?

Розв’язок.

1)Площа квадрата дорівнює 2, отже

Рисунок 3.11

2) Густину імовірності випадкової величини Х знаходимо, використовуючи густину імовірності системи (X,Y):

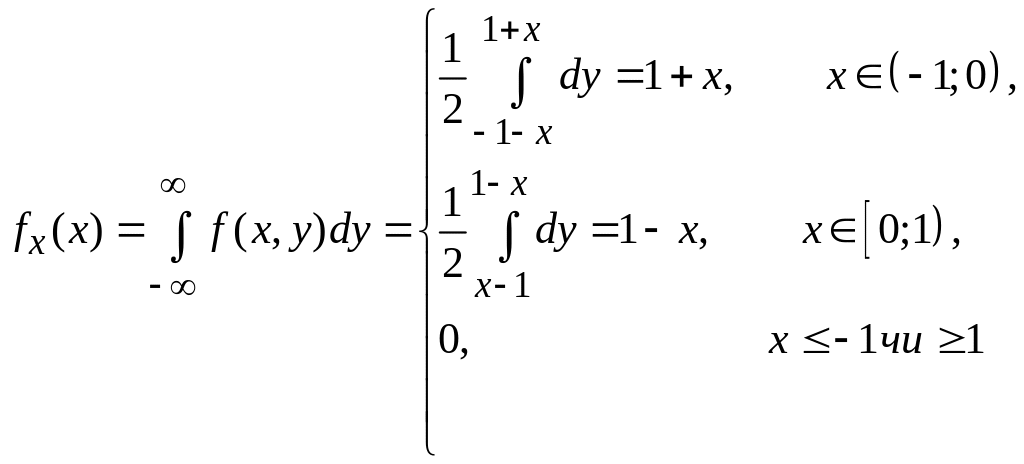
або

3)За аналогією

4)Лише при функція тому

Подібно

Тут ми скористалися тим, що нерівності

задовольняють усі точки, що лежать усередині квадрата R.

5)Випадкові величини X і Y залежні, тому що

6)Випадкові величини X і Y не кореляційні, якщо кореляційний момент

Перевіримо виконання цієї умови. З цією метою обчислимо m_x і m_y:

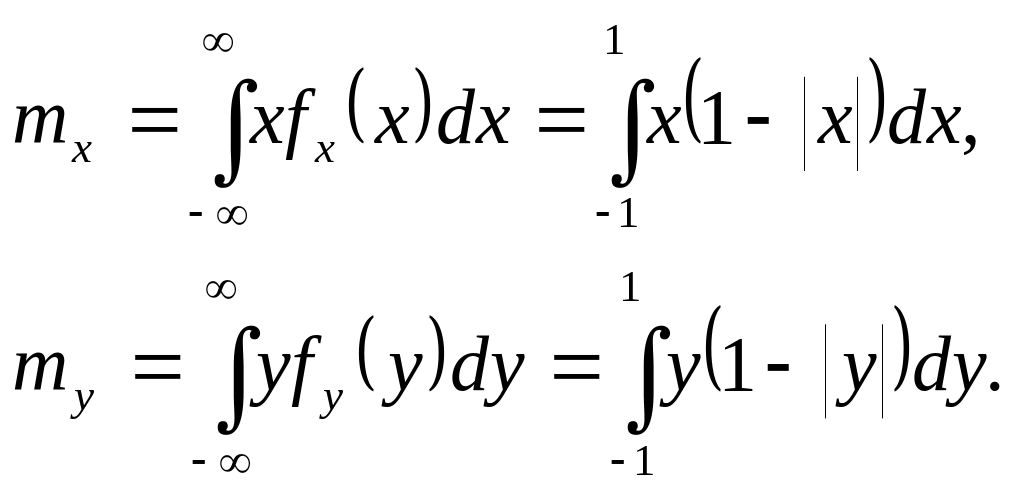
А тому що підінтегральні функції непарні, то

і

Випадкові величини X і Y залежні, але не кореляційні.

4.6. Дано математичні сподівання двох нормальних випадкових величин m_x=4, m_y=-3 і їхню кореляційну матрицю

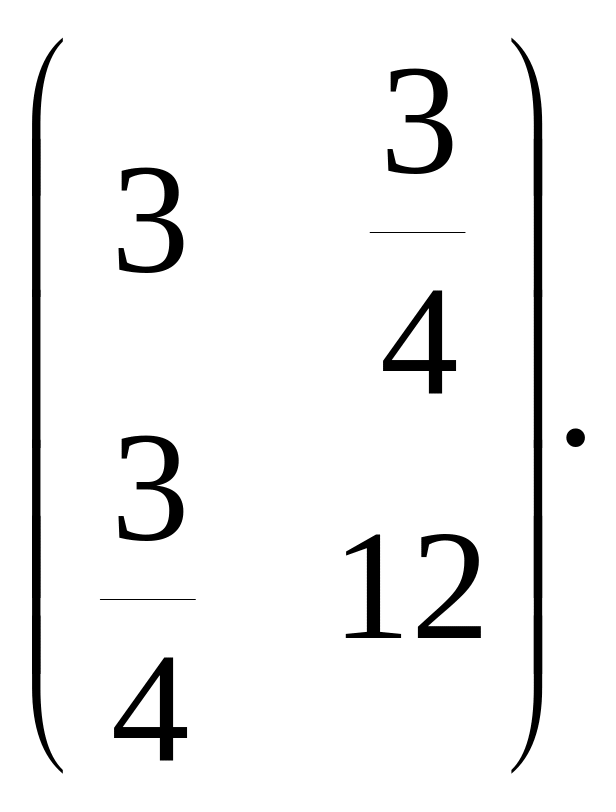
Визначити густину імовірності системи випадкових величин (X,Y).

Розв’язок. Запишемо вираз для густини імовірності системи в загальному вигляді

З кореляційної матриці виходить, що

Отже

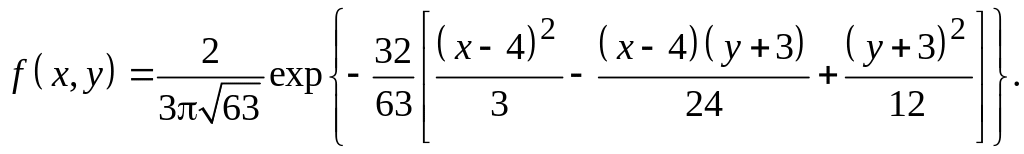
4.7. Нехай густина розподілу системи випадкових величин (X,Y) має вигляд:

Знайти:

1)функцію розподілу системи;

2)математичне сподівання і дисперсію X і Y;

3)кореляційну матрицю.

Розв’язок.

1)Функція розподілу

для різних областей площини матиме різний вигляд. Розглянемо області:

або y<0,

і

і

і

і

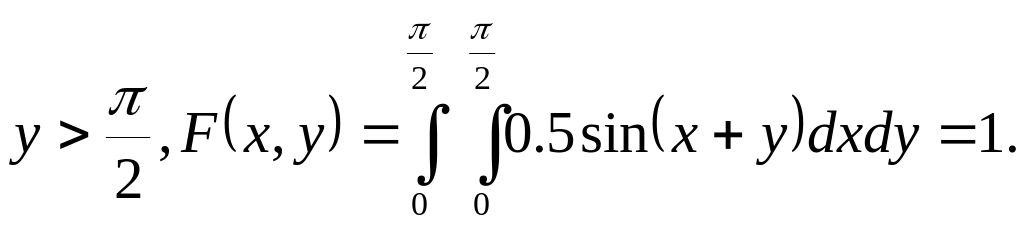
2)Математичне сподівання випадкової величини Х

Дисперсія випадкової величини Х

Із симетрії густини розподілу щодо змінних x і y виходить, що

3)Кореляційна матриця має вигляд

де і кореляційний момент

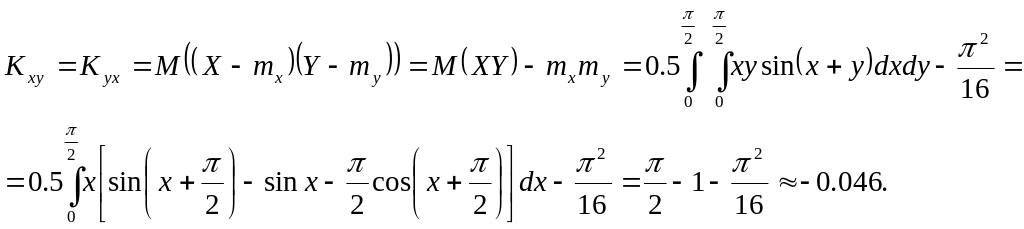
Таким чином, маємо

4.8. Випадкова точка (X,Y) розподілена за нормальним законом на площині:

З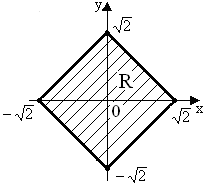 найти імовірності попадання точки (X,Y) у квадрат R ( рис.3.12), сторона якого дорівнює двом.

Розв’язок. Шукана імовірність

Задача полягає в обчисленні подвійного інтеграла. З цією метою розглянемо лінії рівня густини імовірності:

Рисунок 3.12

r

Через те що лінії рівня є колами, то розсіювання кругове. Це означає, що координати випадкової точки (X,Y) не залежать від повороту осей координат. Повернемо осі на , тоді в силу симетрії підінтегральної функції й області інтегрування щодо осей x і y:

4.9. Випадкову точку у просторі задано трьома прямокутними координатами, що складають систему нормальних випадкових величин з густиною імовірності

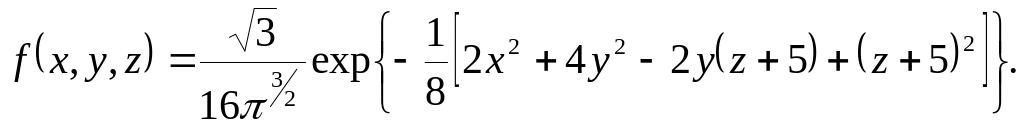
Скласти кореляційну матрицю.

Розв’язок. Задана густина системи трьох випадкових величин факторизується:

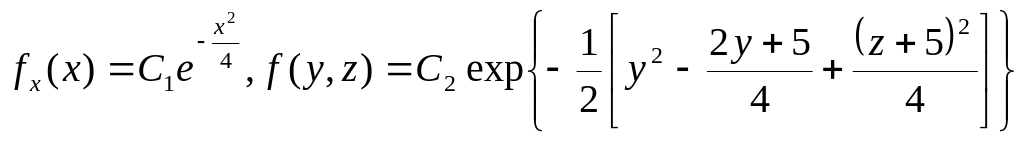
де Це значить, що випадкова величина Х не залежить від Y і від Z. Тому K_xy=0 і K_xz=0. З виразу для густини імовірності випадкової величини Х виходить, що

Густина імовірності нормально розподіленої системи двох випадкових величин (Y,Z) має вигляд

Порівнюючи з отриманою, маємо

Остаточно одержуємо

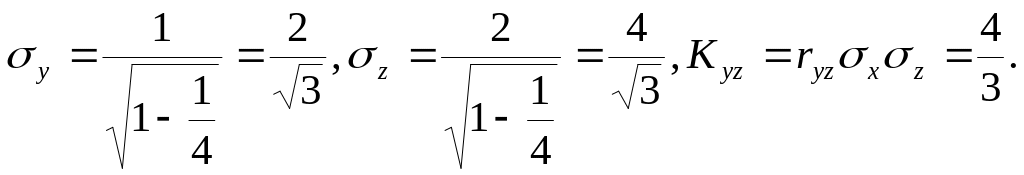
Підставимо отримані результати в кореляційну матрицю

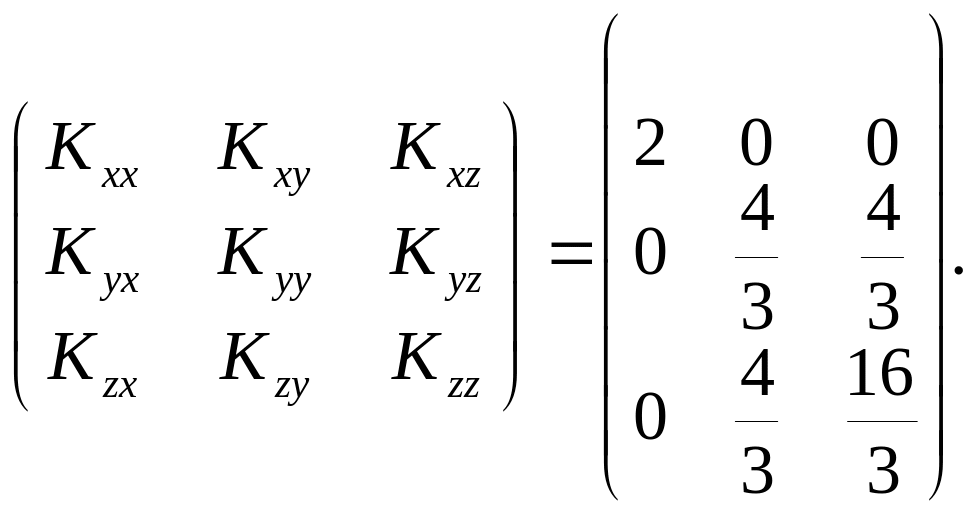
4.10. Дано кореляційну матрицю системи чотирьох нормальних випадкових величин (X₁,X₂,Х₃,Х₄):

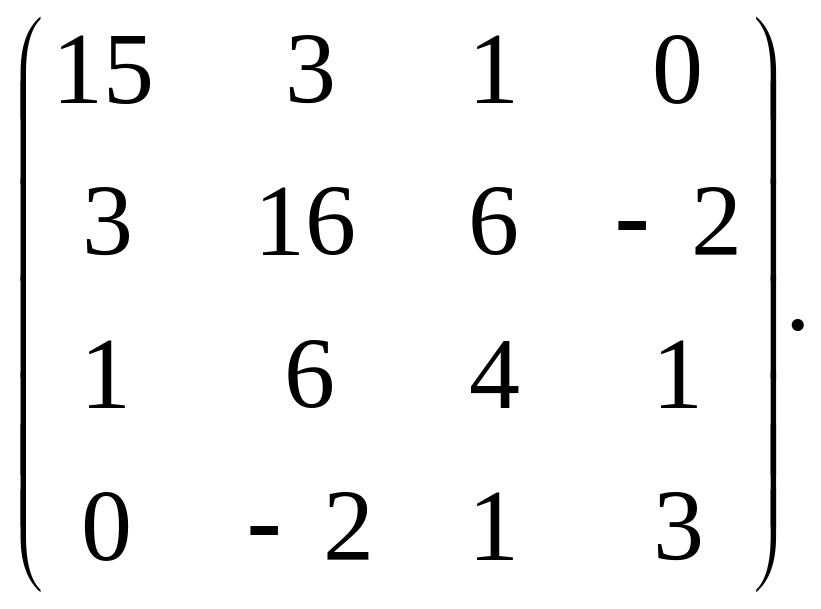
Визначити густину імовірності якщо

Розв’язок. Густина імовірності має вигляд

де - детермінант кореляційної матриці; - елементи оберненої кореляційної матриці; A_ij- алгебричне доповнення елемента K_ij. Обчислюємо алгебричні доповнення:

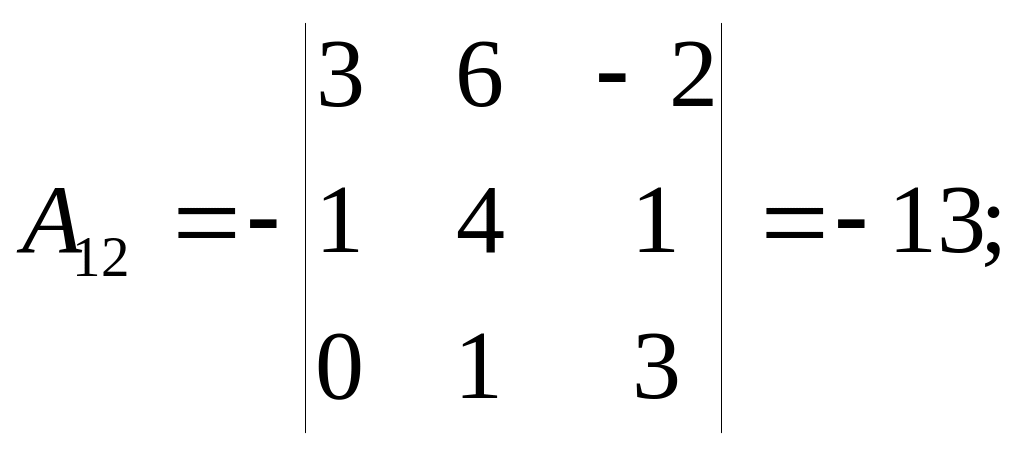
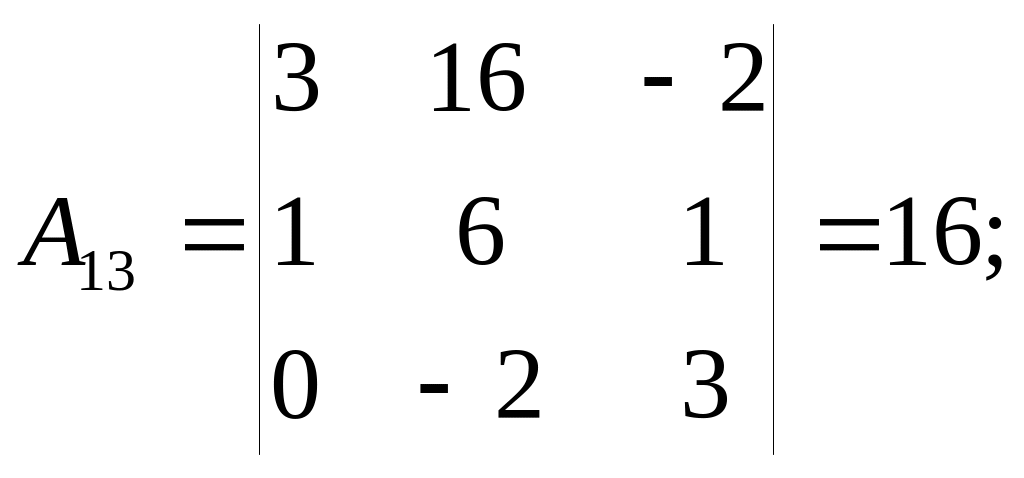
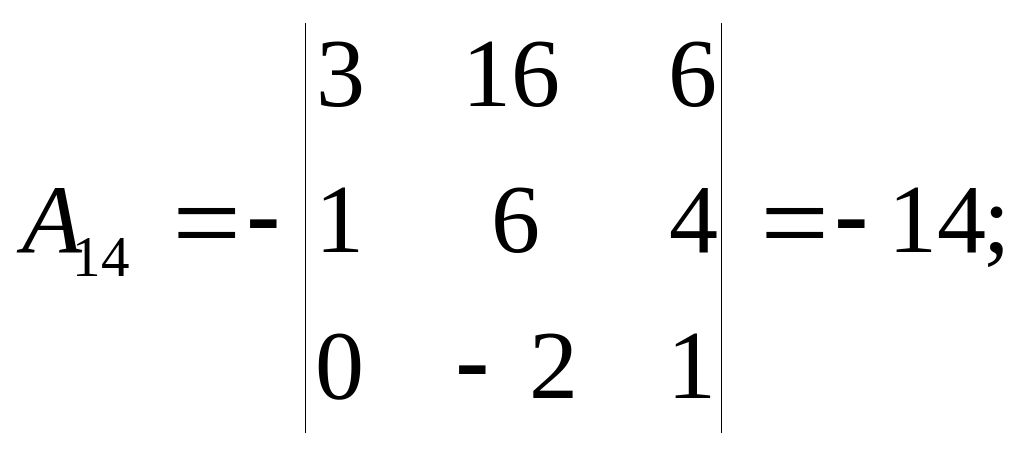
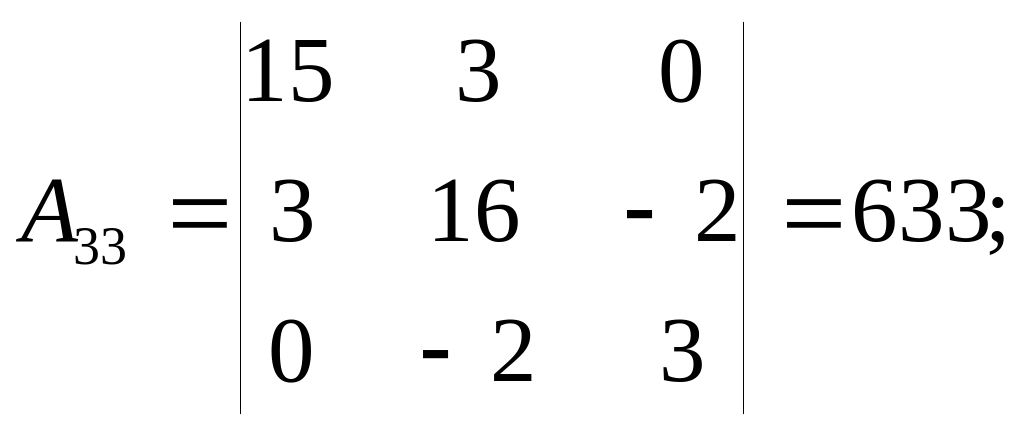
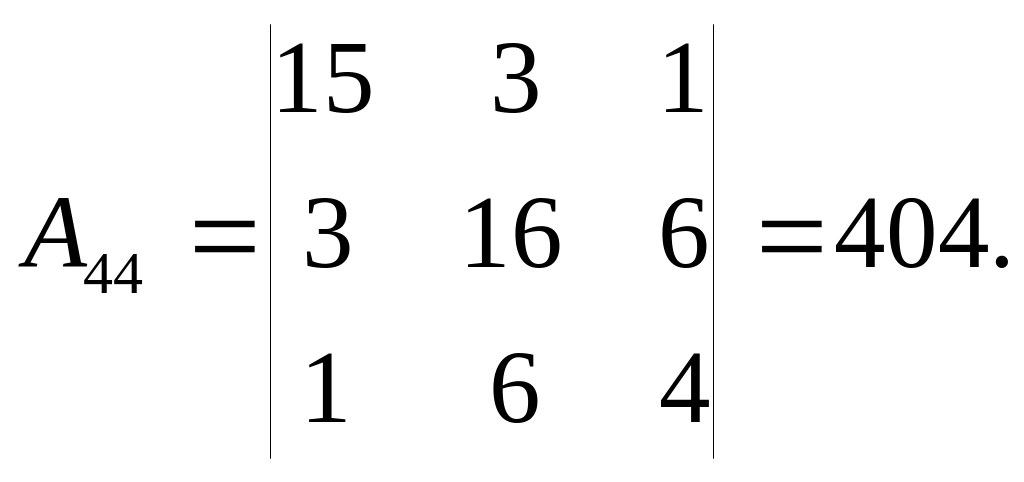
Розкладаючи детермінант по елементах першого рядка, маємо

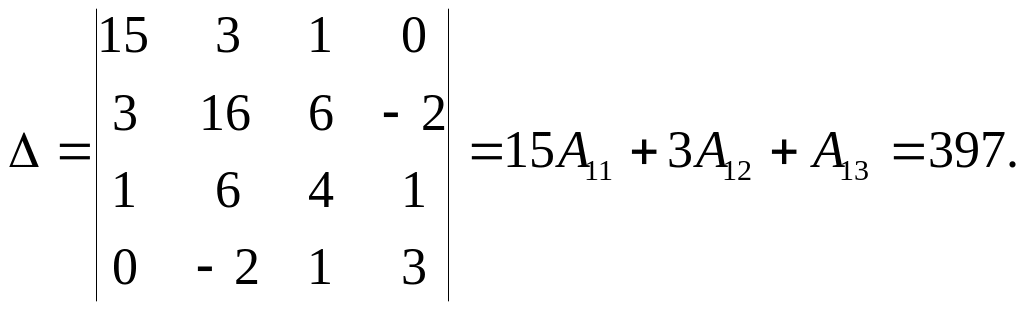
Якщо

то густина імовірності