3.2.2. Задачі

3.19. Випадкова величина Х має густину імовірності (закон Коші)

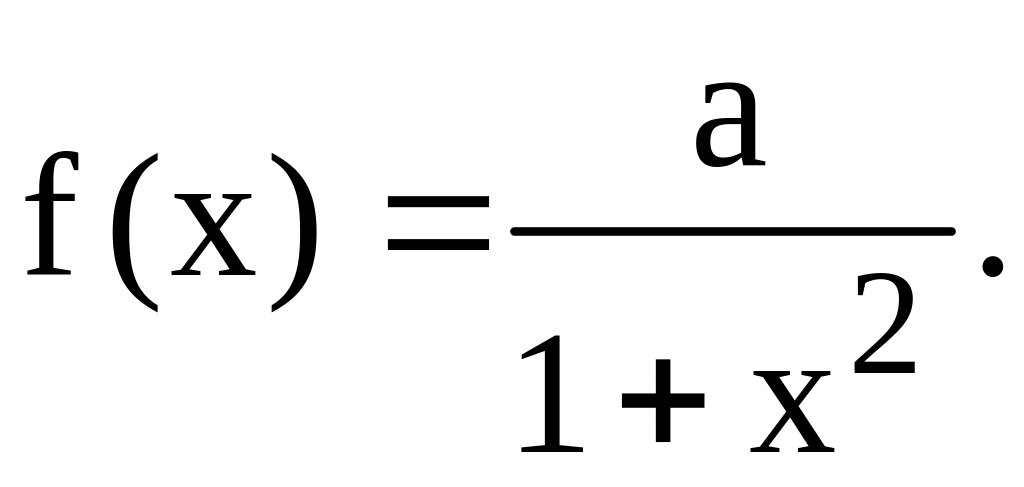
Знайти:

1)коефіцієнт а і функцію розподілу F(x);

2)імовірність нерівності ;

3)математичне сподівання.

3.20. Графік густини імовірності випадкової величини Х зображений нижче (закон Сімпсона). Знайти:

1)густину імовірності цієї випадкової величини;

2)математичне сподівання і дисперсію.

3.21. Функція розподілу імовірності випадкової величини Х має вигляд:

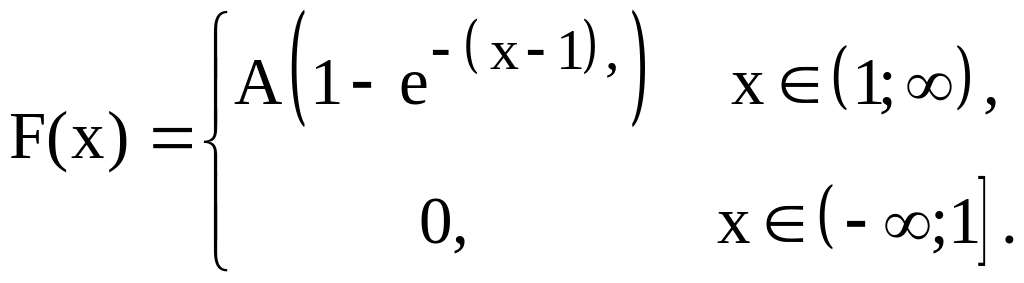
Знайти:

1) F(2);

2) імовірність того, що

3) імовірність того, що .

3.22. Густина імовірності випадкової величини Х задана виразом (закон Релея)

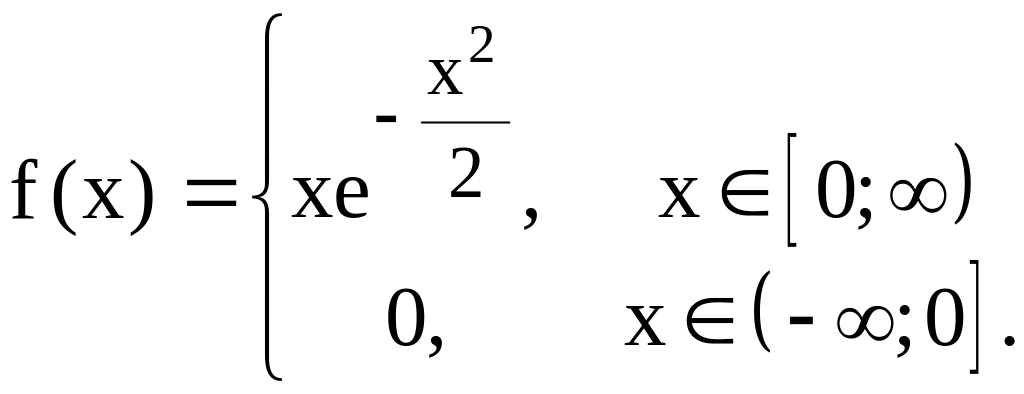
Такому законові розподілу підкоряється амплітуда коливань шумової напруги.

Знайти:

1) найімовірніше значення Х (для якого густина імовірності максимальна);

2) імовірність того, що випадкова величина Х прийме значення, що лежить у границях між (N+5)/(N+10) і (N+5)/(N+1).

3.23. Відхилення величини опору резистора від номінального значення підкоряється нормальному законові розподілу із середнім значенням 10 кОм, рівним номінальному. Середнє квадратичне відхилення дорівнює 200 Ом. Знайти імовірність того, що навмання узятий опір резистора буде відрізнятися від номіналу більш, ніж на (N+1)/100 %.

3.24. Якою середньою квадратичною нормально розподіленою помилкою (максимально припустимою) повинний володіти радіовисотомір, щоб з імовірністю (N+90)/100 помилка при вимірі висоти не перевищувала по абсолютній величині 50 м.

3.25. Випадкова величина Х задовольняє нерівності . Відомо, що кожне зі значень –2 і 2 вона приймає з імовірністю (N+1)/10. Крім того, в інтервалі (-2; 2) випадкова величина має рівномірний розподіл. Знайти функцію розподілу випадкової величини Х.

3.26. Математичне сподівання і дисперсія випадкової напруги з нормальним розподілом рівні 10 В и 25 В² відповідно. Знайти імовірність того, що обмірювана напруга:

1) знаходиться в інтервалі від (N+1)/10 до математичного чекання;

2) у два рази буде більше математичного чекання.

3.3. Функція випадкової величини. Характеристичні функції

Якщо кожному значенню випадкової величини Х ставиться у відповідність значення випадкової величини Y, то Y називається функцією випадкового аргументу Х і записується .

Якщо Х дискретна випадкова величина з рядом розподілу

			…
			…

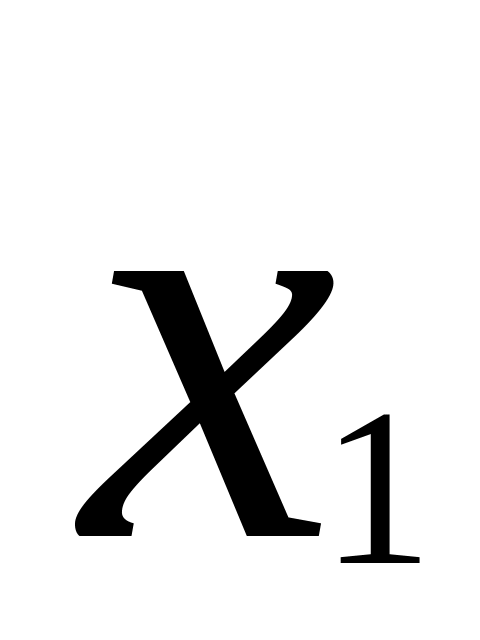
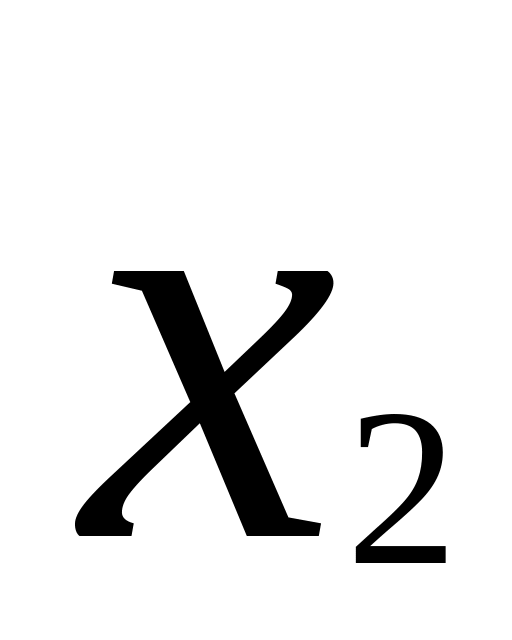
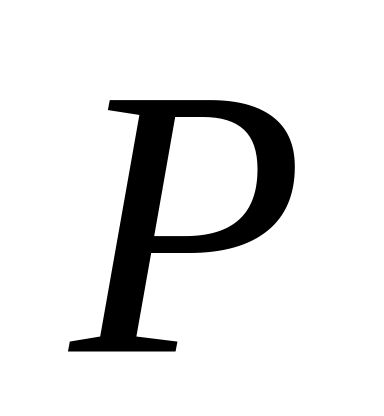
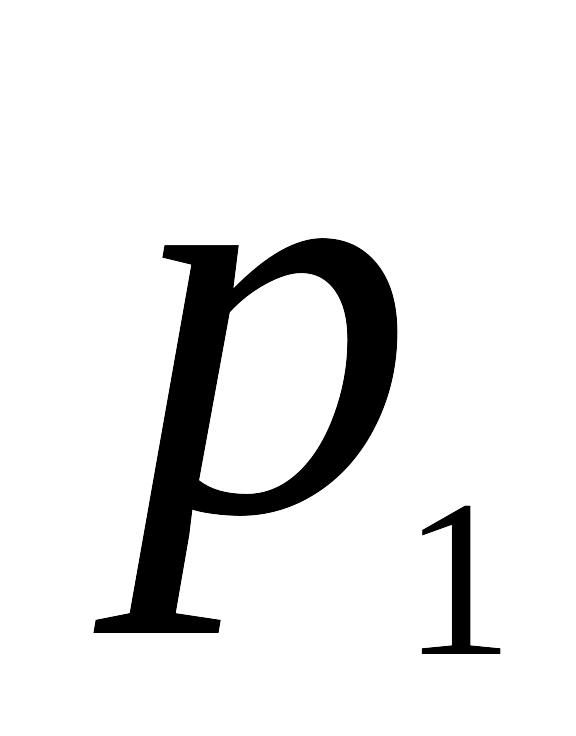
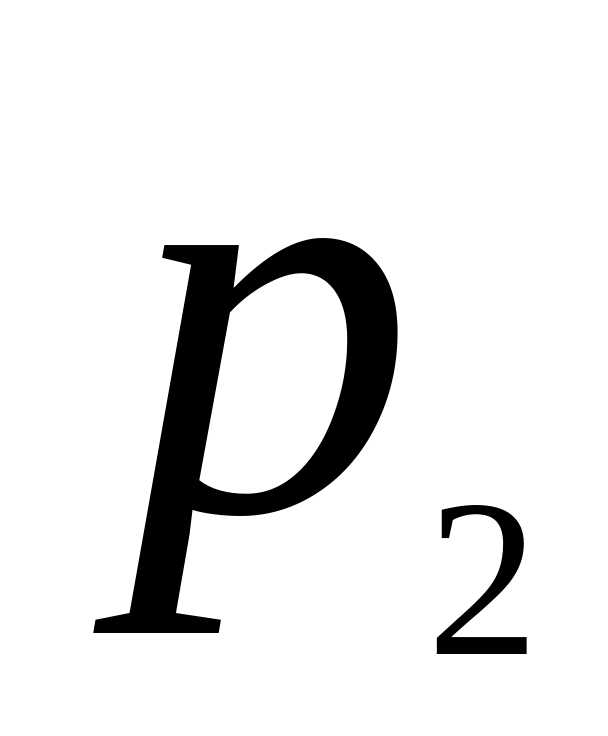
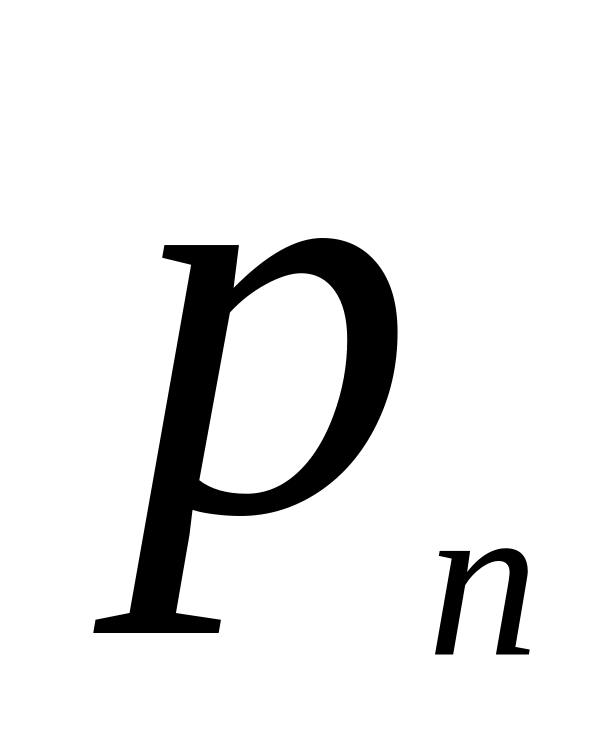
і функція монотонна, то випадкова величина Y також дискретна, що приймає значення , із рядом розподілу

X			…
Р			…

Для немонотонної функції в ряд розподілу однакові значення потрібно віднести до одного стовпця, а відповідні імовірності скласти.

Якщо Х – безперервна випадкова величина із заданою густиною розподілу , і якщо - диференційована монотонна функція, обернена функція якої , то густина розподілу випадкової величини визначається формулою

.

Для немонотонної функції одному значенню відповідають кілька значень аргументу:

,

де - число відрізків, на яких функція є монотонною, а значить на цих відрізках існує обернена функція. Густина розподілу випадкової величини в цьому випадку має вигляд

.

Характеристичною функцією випадкової величини називається математичне сподівання комплексної випадкової величини exp{itX} :

,

де - уявна одиниця.

Для дискретної випадкової величини

,

де .

Для безперервної випадкової величини зі густиною розподілу характеристична функція

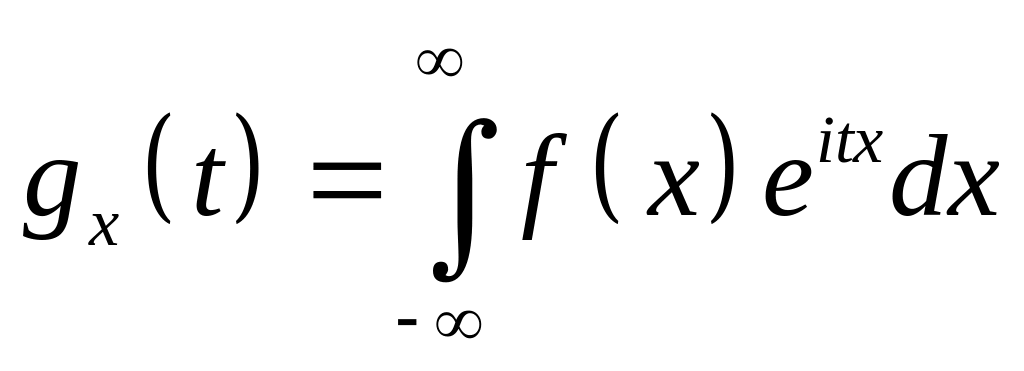
є перетворенням Фур'є густини розподілу. За допомогою оберненого перетворення Фур'є можна знайти густину розподілу

.

Відзначимо, що і для кожного .

Якщо випадкові величини і зв'язані між собою співвідношенням , де - невипадковий множник, то їхні характеристичні функції зв'язані співвідношенням

.

Якщо випадкова величина являє собою суму незалежних випадкових величин

,

То

,

тобто характеристична функція суми незалежних випадкових величин дорівнює добутку характеристичних функцій доданків.

3.3.1 Приклади розв'язання задач

27. Дискретна випадкова величина Х має ряд розподілу

X	3	6	10
P	0,2	0,1	0,7

Знайти ряд розподілу випадкової величини .

Розв’язок. Випадкова величина приймає значення:

.

Бачимо, що різним значенням Х відповідають різні значення Y. Це пов'язано з тим, що функція монотонна.

Коли випадкова величина Х приймає значення 3, випадкова величина Y приймає значення 10. Вірно і зворотне твердження. Це говорить про рівнозначність цих подій. Отже,

.

Аналогічно отримаємо імовірності інших можливих значень величини Y:

,

.

Таким чином ряд розподілу Y має вигляд:

Y	10	19	31
P	0,1	0,2	07

3.28 Дискретна випадкова величина Х має ряд розподілу

X	-1	0	1	2
P	0,2	0,1	0,3	0,4

Знайти ряд розподілу випадкової величини .

Розв’язок. Знайдемо можливі значення Y:

Отже, різним значенням і відповідає одне значення . Це пояснюється тим, що ці значення Х належать інтервалові, на якому функція немонотонна.

Знайдемо імовірності можливих значень величини Y. Випадкова величина Y приймає значення 1, коли випадкова величина Х приймає значення -1 або 1. Останні дві події несумісні і їхні імовірності відповідно рівні 0,2 і 0,3. Тому

.

Іншим значенням Y відповідає одне значення Х:

.

Тепер можна записати ряд розподілу випадкової величини Y:

Y	-1	1	0,7
P	0,1	0,5	0,4

3.29 Випадкова величина Х рівномірно розподілена в інтервалі . Знайти густину розподілу випадкової величини .

Розв’язок. Функція в інтервалі монотонна, тому густину розподілу величини Y знаходимо по формулі

.

Коли величина Х приймає значення в інтервалі , випадкова величина Y змінюється в межах (-1;1). Поза цим інтервалом густина розподілу в силу неможливості випадкової величини Y прийняти там яке-небудь значення. Тому що , то

. ( )

Для одержання шуканої величини скористаємося густиною розподілу величини Х:

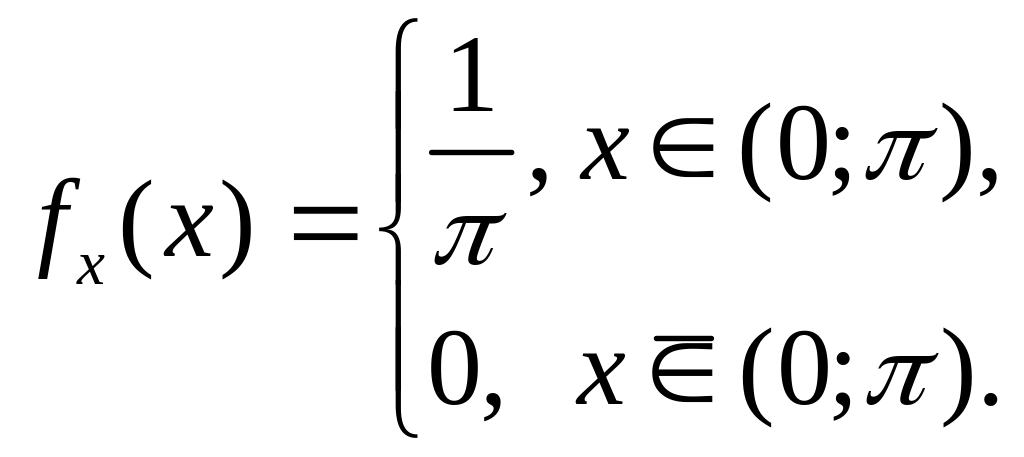
і співвідношенням ( ):

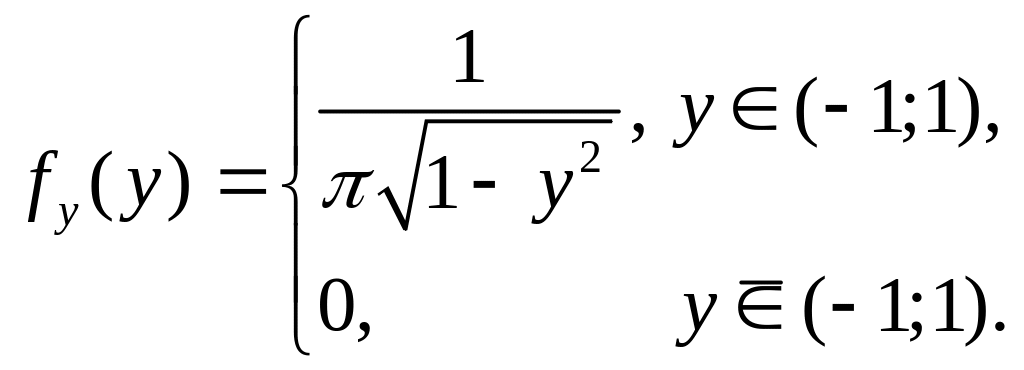
3.30 Знайти густину розподілу випадкової величини Y – опору паралельного з'єднання двох резисторів, один із яких має фіксований опір R, у той час як опір другого резистора Х – випадкова величина, рівномірно розподілена в інтервалі , де - постійне число.

Розв’язок. Насамперед знайдемо функціональну залежність між випадковими величинами Y і Х. Оскільки резистори з'єднані паралельно, то

.

Звідси отримаємо, що . Функція монотонна, тому що

.

Тому будемо користуватися формулою:

, ( )

де випадкова величина Y приймає значення в інтервалі . Для того, щоб скористатися цією формулою знайдемо обернену функцію до функції , а також її похідну:

і густину розподілу випадкової величини Х:

.

Підставивши отримані величини у формулу ( ), одержуємо шукану густину:

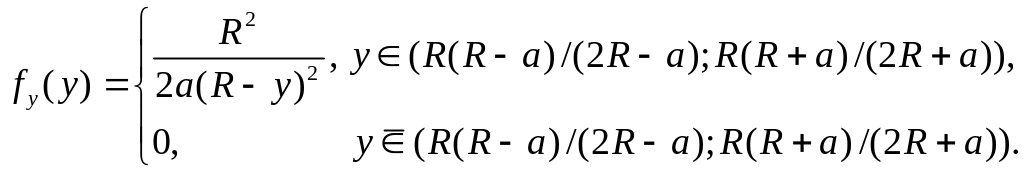
3.31 У системах зв'язку загасання сигналу при проходженні його по тракті виражається як

,

де і - потужність вихідного і вхідного сигналів. З експериментів відомо, що загасання часто поводиться як нормальна випадкова величина. Знайти густину розподілу випадкової величини , вважаючи, що являє собою нормальну випадкову величину з математичним сподіванням і дисперсією .

Розв’язок. Випадкова величина зв'язана з випадковою величиною функціональною залежністю

.

Функція - монотонна позитивна функція для всіх дійсних значень змінної величини , тому зворотна функція однозначна і, вирішуючи задачу за правилом для монотонної функції, одержуємо

Така густина розподілу величини називається логнормальною.

3.32 Випадкова напруга Х прикладена до резистора опором R. Знайти густину розподілу потужності Y, яка розсіюється на цьому опорі, якщо відомо, що нормована випадкова величина Х підлегла нормальному законові розподілу. (Нормованою випадковою величиною називають величину, у якої математичне сподівання дорівнює нулю, а дисперсія - одиниці).

Розв’язок. Залежність між величинами Y і Х немонотонна, тому що потужність . Одному значенню відповідає два значення x: , , причому . Тому скористаємося для визначення шуканої густини формулою:

,

де

і Після простих перетворень маємо:

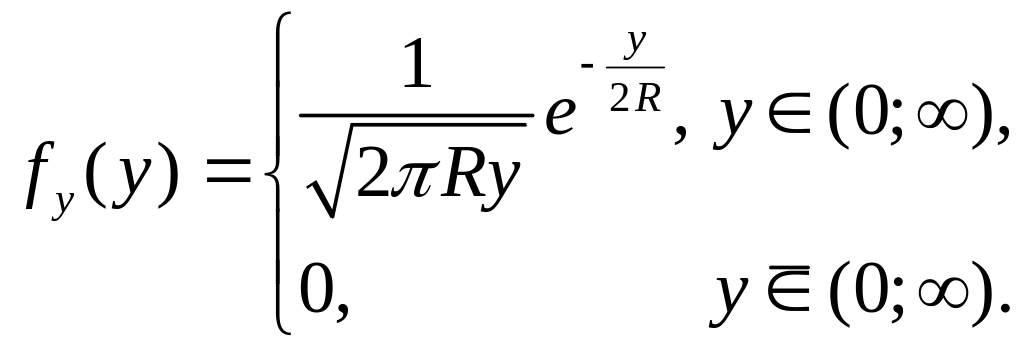
3.33 Якому функціональному перетворенню потрібно піддати випадкову величину Х, рівномірно розподілену в інтервалі (0;1), щоб одержати випадкову величину Y, розподілену по показовому законі

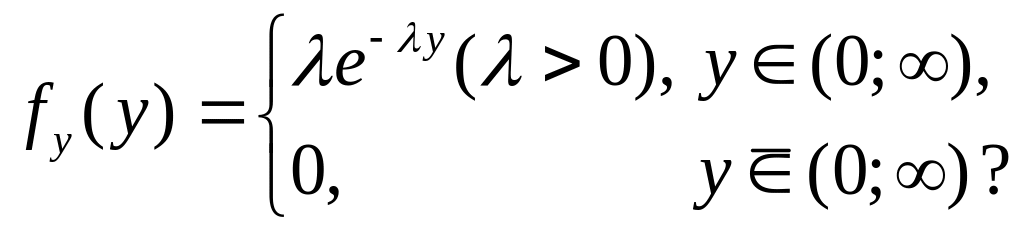
Розв’язок. Будемо знаходити шукану залежність між величинами Y і Х у вигляді монотонної зростаючої функції , для якої за умовою задачі

.

Проінтегруємо ліву і праву частину співвідношення

від 0 до y, вважаючи . Тоді

.

Відкіля отримуємо потрібну залежність

.

3.34 Є випадкова величина Х, що підкоряється законові Релея:

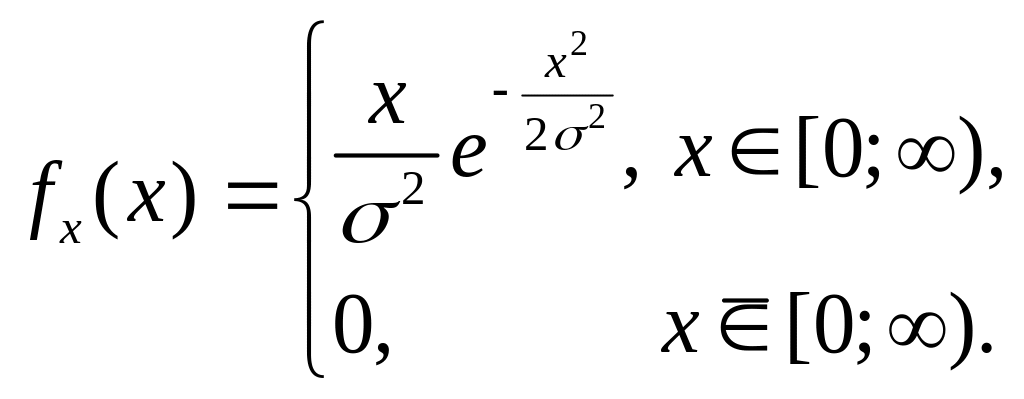
Випадкова величина Y визначається через Х співвідношенням

Це значить, що Y=X при і при . Знайти густину розподілу випадково величини Y.

Розв’язок. Випадкова величина Y є величиною змішаного типу – безперервною при y<1 і дискретною, приймаючи одне значення, що дорівнює одиниці, для . При y=1 її функція розподілу має скачок , який дорівнює імовірності того, що випадкова величина Х прийме значення більше одиниці:

.

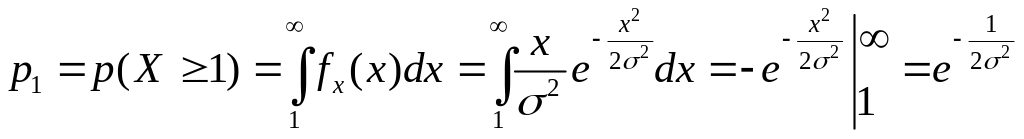При густина розподілу випадкової величини Y буде збігатися з густиною розподілу випадкової величини Х. Тому шукана густина має вигляд

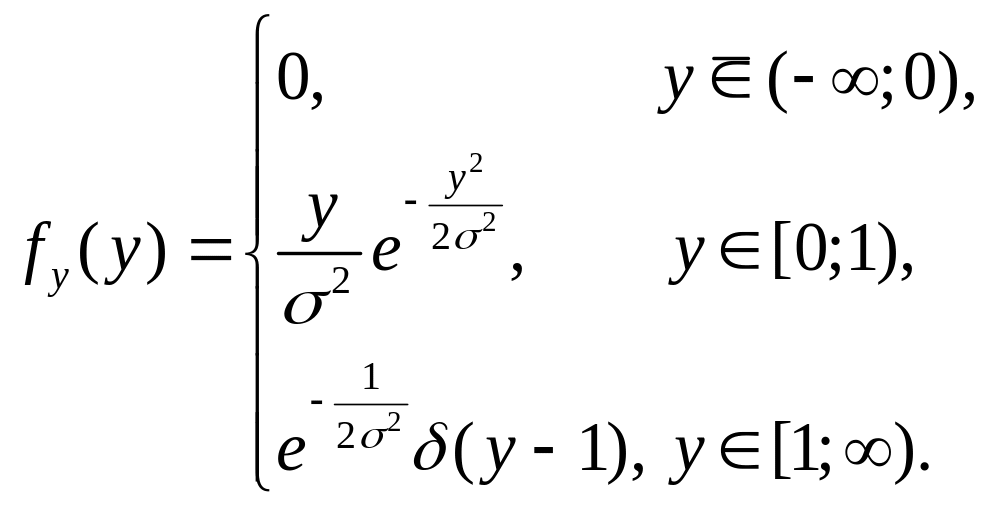
3.35 У партії, що складається з мікросхем, виробів мають дефект. Для перевірки якості зроблена вибірка мікросхем . Визначити характеристичну функцію числа дефектних мікросхем, що утримуються у вибірці.

Розв’язок. Випадкова величина - число дефектних мікросхем, що містяться у вибірці, - може приймати значення від до . Позначимо

.

Тому як

,

то характеристична функція

.

3.36 Знайти характеристичну функцію випадкової величини, підлеглої законові Пуассона

.

Розв’язок. Характеристична функція

.

Відомо що

,

де в нашому випадку , тоді

.

3.37 Знайти характеристичну функцію випадкової величини , густина імовірності якої

,

і по ній знайти і .

Розв’язок. Запишемо формулу характеристичної функції для безперервної випадкової величини :

.

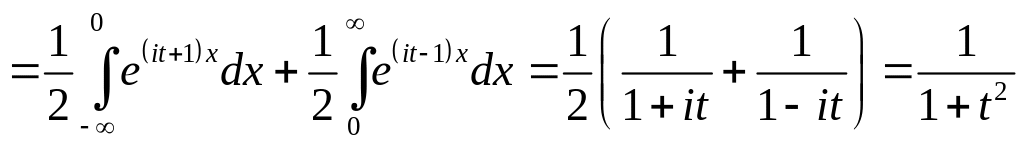Обчислимо першу і другу похідні характеристичної функції в нулі випадкової величини з довільною густиною імовірності :

,

.

Значить

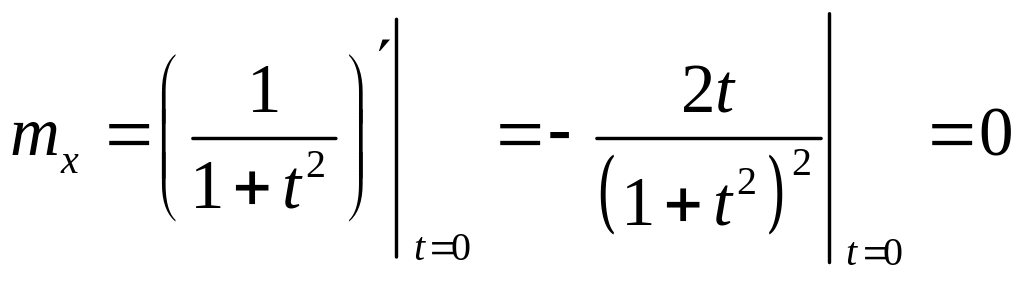
(це безпосередньо випливає з парності функції густини імовірності) і

.