4. Система випадкових величин

4.1 Закони розподілу і числові характеристики системи випадкових величин

Системою двох випадкових величин (Х,Y) називається сукупність випадкових величин Х і Y, що спільно розглядаються . Систему двох випадкових величин можна розглядати як випадкову точку з координатами (Х,Y) прямокутної декартової системи координат.

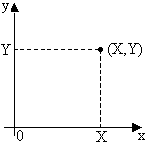
Функцією розподілу F(x,y) системи двох випадкових величин (X,Y) називається імовірність того, що в результаті проведення досліду випадкова величина Х набуває значення, менше ніж х, а випадкова величина Y – менше ніж y:

.

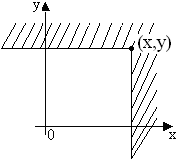
Тобто, функція розподілу - це імовірність того, що внаслідок проведеного експерименту випадкова точка потрапляє в не штриховану область.

Властивості функції розподілу:

1) ;

2) ;

;

3)

де , - відповідно функції розподілу випадкових величин Х і Y;

4) - неспадаюча функція однієї змінної при фіксованій другій;

5) імовірність улучення випадкової точки (X,Y) у прямокутник R з координатами вершин (x₁,y₁), (x₁,y₂), (x₂,y₁), (x₂,y₂) прямокутної системи координат ХOY виражається через функцію розподілу формулою

.

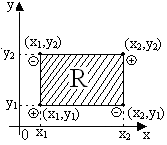
Рисунок 3.3

.

Густиною розподілу системи двох випадкових величин (X,Y) називається функція , рівна другій змішаній похідній від функції розподілу :

.

Поверхня, що зображує функцію , називається поверхнею розподілу.

Властивості густини розподілу:

1) ;

2) ;

3) ;

4) ,

де , - густини розподілу випадкових величин X і Y;

5) 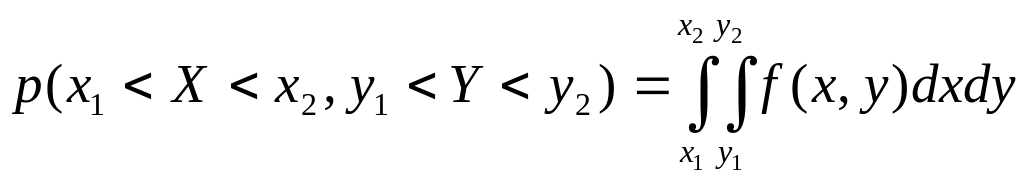. (3.1)

Основними числовими характеристиками системи двох випадкових величин (Х,Y) є математичні сподівання

,

,

дисперсії

,

і кореляційний момент.

Кореляційним моментом К_xy випадкових величин Х і Y називається математичне сподівання добутку центрованих випадкових величин і :

.

Коефіцієнтом кореляції випадкових величин Х і Y називається безмірна величина

,

де , - середньоквадратичні відхилення величин X і Y.

Коефіцієнт кореляції характеризує ступінь тісноти лінійної залежності між випадковими величинами.

Випадкові величини Х і Y називаються некорельованими, якщо їхній кореляційний момент (або, що рівнозначно, коефіцієнт кореляції ) дорівнює нулю.

З незалежності випадкових величин виходить їхня некорельованість; навпаки, з некорельованості випадкових величин не виходить їхня незалежність.

Якщо випадкові величини Х і Y зв'язані лінійною залежністю

,

то їхній коефіцієнт кореляції , де знак + або – береться відповідно зі знаком коефіцієнта a.

Для будь-яких випадкових величин

.

Математичним сподіванням функції g(X,Y) випадкових величин Х і Y називається величина

.

Система двох випадкових величин (X,Y) називається нормально розподіленою (нормально розподіленою на площині), якщо густина розподілу

,

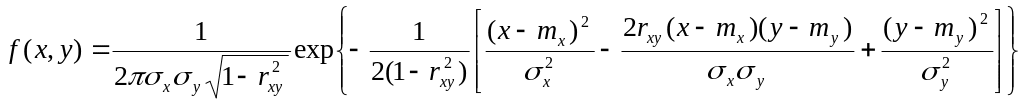де m_x, m_y - математичні сподівання випадкових величин Х і Y;

- їх середньоквадратичні відхилення;

- їхній коефіцієнт кореляції.

Системою n випадкових величин (Х₁,Х₂,…,Х_n) називається сукупність n випадкових величин Х₁,Х₂,…,Х_n, що спільно розглядаються.

Функцією розподілу системи n випадкових величин (Х₁,Х₂,…,Х_n) називається імовірність спільного виконання n нерівностей вигляду

:

.

Властивості функції розподілу :

1) ;

2) ;

3) - функція розподілу випадкової величини Х₁;

4) - функція розподілу системи двох випадкових величин (Х₁,Х₂);

5) - функція розподілу системи n-1 випадкових величин (Х₁,Х₂,…,Х_n-1);

6) ;

7) - неспадаюча функція однієї змінної при фіксованих інших.

Густиною розподілу системи n випадкових величин називається змішана похідна n-го порядку функції розподілу:

.

Властивості густини розподілу:

1) ;

2) ;

3) ;

4) ,

де - густина розподілу системи випадкових величин Х₁,Х₂,…,Хm.

Основними числовими характеристиками системи n випадкових величин (Х₁,Х₂,…,Х_n) є математичні сподівання

,

дисперсії

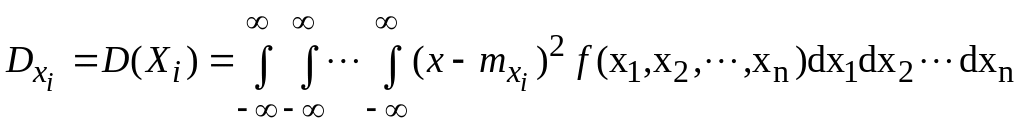
і кореляційна матриця К.

Кореляційною матрицею К системи n випадкових величин (Х₁,Х₂,…,Х_n) називається таблиця, складена з кореляційних моментів усіх цих величин, узятих попарно

,

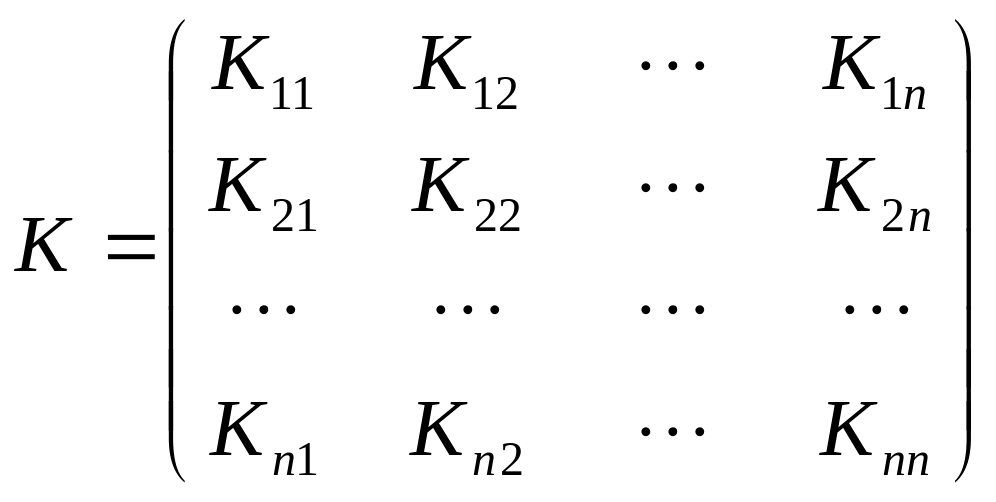де - кореляційний момент випадкових величин X_i і X_j.

Кореляційна матриця симетрична . По головній діагоналі кореляційної матриці розміщені дисперсії випадкових величин Х₁,Х₂,…,Х_n:

.

Нормованою кореляційною матрицею R системи n випадкових величин називається таблиця, складена з коефіцієнтів кореляції всіх цих величин, узятих попарно

,

де - коефіцієнт кореляції випадкових величин Х_i і Х_j.

Густина імовірності для системи n нормально розподілених випадкових величин (Х₁,Х₂,…,Х_n) має вигляд

,

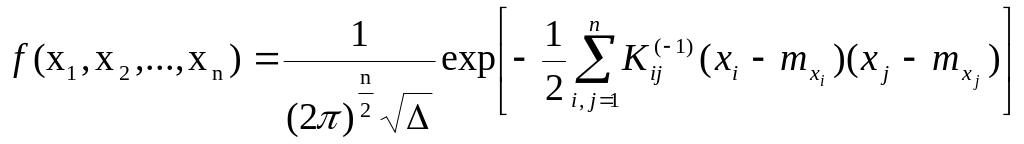де

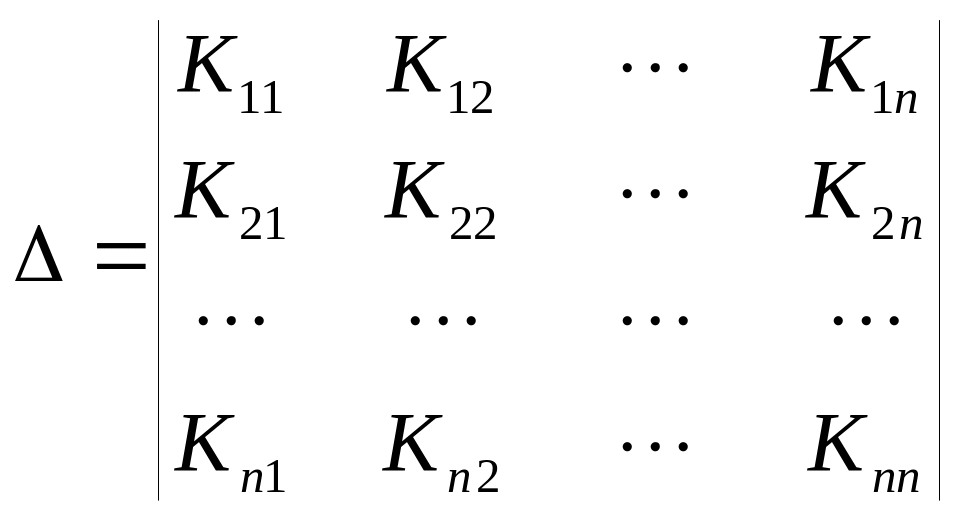
- детермінант, складений з елементів кореляційної матриці; - елементи оберненої кореляційної матриці:

;

A_ij – алгебричне доповнення елемента К_ij.

В окремому випадку для системи трьох незалежних нормально розподілених випадкових величин (X,Y,Z) маємо і

.

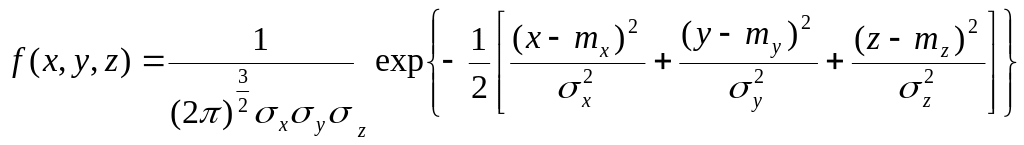Умовною функцією розподілу випадкової величини Х за умови, що подія М відбулася , називається функція, рівна відношенню імовірності появи спільної події X<x і М до імовірності появи події М:

.

Умовні функції розподілу для окремих випадків події М:

1) = - подія, яка полягає в тому, що в результаті проведення досліду випадкова величина Y прийме значення менше, ніж y, тоді

;

2)

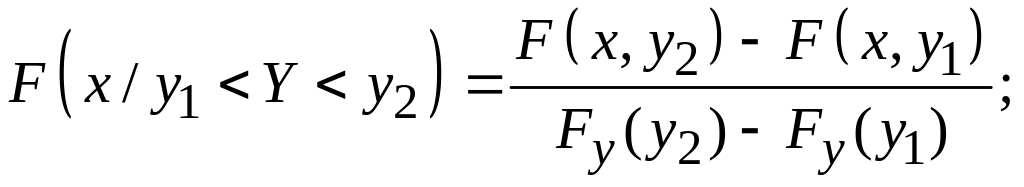
3) .

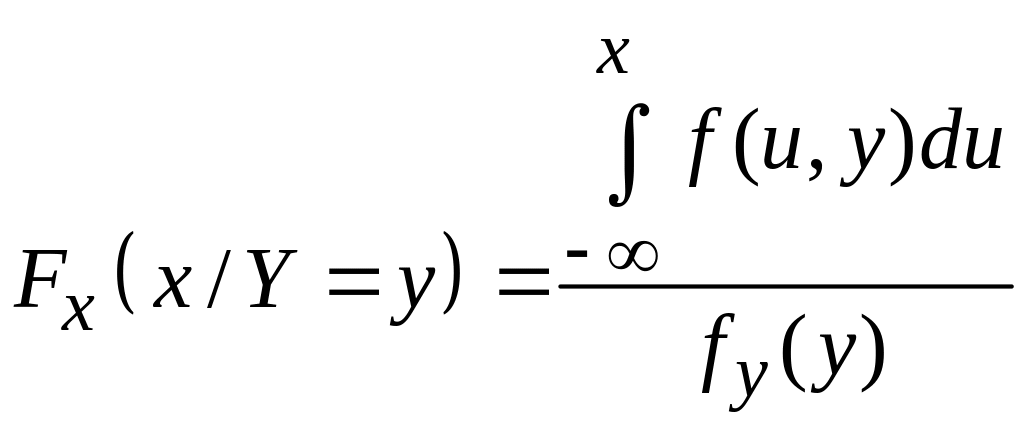Умовною густиною розподілу випадкової величини Х за умови, що подія М відбулася , називається похідна від умовної функції розподілу

.

Позначимо , , тоді

,

.

Звідси виходить аналог формули Байєса

.

Випадкові величини Х і Y незалежні, якщо густини розподілу системи (X,Y) факторизуються:

.

Умовною густиною розподілу системи випадкових величин за умови, що випадкові величини X_m+1=x_m+1, X_m+2=x_m+2,…,X_n=x_n, називається густиною розподілу ,яка дорівнює відношенню густини розподілу системи (Х₁,Х₂,…,Х_n) до густини розподілу системи (Х_m+1,Х_m+2,…,Х_n):

.

Випадкові величини незалежні, якщо густина розподілу системи факторизується:

,

де - густина розподілу випадкової величини Х_i.