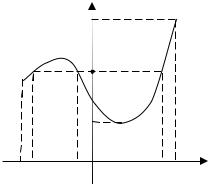
у

По

теореме

о

промежуточных

y f x

М

значениях

f x

принимает

все

промежуточные значения между m

и M ,

в

том

числе и значение

m

1

b

f x dx.

Таким

образом,

b a a

a c1

c2 О

c3 b x

существует по крайней мере одна

точка c a, b ,

такая, что

Р с. 3.2

С

1

b

и

f c

f x dx.

b a a

Что и требовалось доказать.

3.2. Формула Ньютона – Лейбница

Рассмотрим

функцию

y f x .

Значение

определённого

b

интеграла от этой

функции

f x dx

зависит от пределов a

и b.

a

бА

b

f x dx

будет

Если зафиксировать значение

a,

то

величина

a

зависеть только от числа b. Зафиксируем нижний предел

интегрирования a, а верхний будем считать переменным.

Чтобы

подчеркнуть

переменность

верхнегоДпредела интегрирования,

её с верхним пределом, заменим переменную x

внутри интеграла на

переменную t.

И

x

Таким образом, получим функцию

x f t dt. Она

a

пределом). Пусть интегрируемая на отрезке a, b функция

y f x

x

С

a

Доказательство. По определению производной,

x lim

x x x

.

x

x 0

интеграла

Расп шем функц ю

x x

x

x x

x x

x x

f t dt f t dt f t dt x f t dt .

a

a

x

x

бА

6

определенного

Здесь мы

воспользовались

свойством

. Пр мен м теорему о среднем значении и получим

x x

x x x

f t dt f c x,

x

где c – между x

и

x x. Следовательно,

f c

x

x ,

f

x lim

x 0

x

так как c x, когда x 0. Что и требовалось доказать.

Замечание.

Из

Д

из

теоремы следует,

что

x

–

одна

x f

x .

первообразных функции f x на отрезке a, b , так как

Значит, если

функция

F x

–

другая

первообразная,

то

x F x C.

И

Теорема (Ньютона – Лейбница). Пусть функция

y f x

непрерывна x a, b

и F x – одна из её первообразных. Тогда

b

b

f (x)dx F(x)

F(b) F(a).

a

a

Формула называется формулой Ньютона–Лейбница.

x

Доказательство.

Рассмотрим

функцию

x f t dt.

По

a

теореме о производной определённого интеграла с переменным

верхним пределом,

она является первообразной для

f x

на a, b .

f x , то x F x C x a, b .

При

x a

получим выражение

Ф(a) F(a) C,

из которого

C Ф(a)- F(a),

a

выразим

постоянную

но

т.к. Ф(a) f (t)dt 0,то

C -F(a).

a

b F b C F b F a ,

При

x b

находим

откуда

b

f t dt F b F a .

и

a

СПереобознач в

переменную

интегрирования,

получим

требуемую формулу

b

бА

f

x dx

F b F a .

a

1

dx

3

dx

Пр мер 1. Выч слить интегралы

x2

и

x2

.

1

4

Решение. Если использовать для вычисления первого интеграла

1

dx

1

формулу Ньютона– Лей ница, то получается, что

1

1

2 0.

x2

x

1

1

Но подынтегральная

функция

y

0,

поэтому

полученный

2

x

результат противоречит свойству 4 определённого интеграла.

Причина этого в том, что функция

y

1 имеет в точке x 0 1,1

x2

И

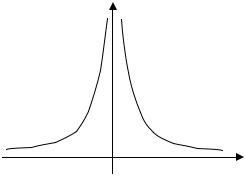
разрыв второго рода (рис. 3.3), т. е. не является на отрезке

у

Д1,1 интегрируемой, а значит,

формулу

Ньютона–Лейбница

1

применить

здесь

нельзя.

Но

y

x 4, 3

она

непрерывна, поэтому

2

x

для

вычисления

второго

интеграла

формулу Ньютона-Лейбница применить

можно:

О

х

3

1

3

1

1

1

dx

.

4

x2

x

3

4

12

4

2

f x dx

Пример

2. Вычислить

от

функции,

заданной на

отрезке 2, 2

2

двумя аналитическими выражениями:

x 2,

2 x 0 ;

у

f x

2

С

x 2

,

0 x 2

4

(рис. 3.4).

2

Решение.

Для

вычисления

такого

интеграла

надо

и

воспользоваться

свойством

6

определенного интеграла:

-2

О

2

х

бА

Р с. 3.4

2

0

2

(x 2)

2

0

3

2

14

f (x)dx (x 2)dx

(x 2)2dx

.

2

2

0

2

2

3

3

4

3

0

x

Пример 3. Вычислить 1 4x

dx.

2

3

1

Д

Решение. Используя свойства 1 и 7, представим определенный

интеграл в виде суммы трех более простых интегралов, к каждому из

которых применим формулу Ньютона – Лейбница

4

3

x

4

4

3 4

1

1 4x

2

dx dx 4 xdx

x2 dx

1

4

1

1

21

x2

3

x

2

2

4

(x

4

)

(x 2x

x

3

)

2

2

3

1

) 3И30 7 20.

2

1

(4 1) 2(42

12) (

43

13