3.ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ

Пусть дана функция

f x ,

непрерывная

на отрезке

a;b , где

С

a b и f x

0 x a, b .

у

и

В

y f x

бА

А

x0 a x

О

xi 1 xi

x

b x

х

1

i

n

Д

Рис.3.1

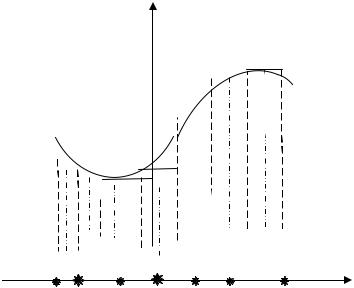
Назовём фигуру, ограниченную кривой

f x ,

прямыми

x a;

x b и отрезком оси Ox, криволинейной трапецией (рис. 3.1).

Выполним следующие действия:

И

1) разобьём отрезок a;b произвольным образом на n

частичных

отрезков длиною

xi

i 0,1,2,...,n ,

так

что

a x0 x1 x2 ... xn 1 xn

b;

отрезке xi 1;xi

2) выберем в каждом частичном

по

одной

зависят от числа разбиений n

и от выбора точек деления xi

и точек

ci xi 1;xi .

При

этом оказывается,

что

все

эти

различные

интегральные

суммы

при

неограниченном

возрастании

n

и при

стремлен

к нулю на большей из длин частичных отрезков имеют

общий предел.

С

при любой последовательности разбиений

Определен е.

отрезка, a;b

так х, что max xi 0

n , при любом выборе

точек ci xi 1;xi

нтегральная сумма n

n

ci xi

f

стремится к

Если

A:lim

i 1

f c

x A,

lim

одному

тому же конечному числу

0

n

0

n 1

i

i

то число A называется определенным интегралом от функции

f x на

b

отрезке a;bби о означается f x dx.

a

b

n

Итак, по определению,

f (x)dx lim

f (ci ) xi .

a

0

i 1

Числа

a

и

Аb называются пределами

интегрирования:

a нижним,

b верхним.

Отрезок

a;b

называется

отрезком

интегрирования.

Функция

f x

называется

подынтегральной

функцией, а переменная x переменной интегрирования.

Геометрический

смысл

определенного интеграла на отрезке:

Д

определенный интеграл от неотрицательной на отрезке a,b

функции

численно равен площади криволинейной трапеции, ограниченной

графиком функции и отрезком a,b оси абсцисс.

Замечание. Очевидно,

b

b

И

что f x dx f

t dt

, т. е. переменную

a

a

a

Таким образом, всякая кусочно-непрерывная на заданном

С

отрезке функция интегрируема на этом отрезке.

Свойства определенного интеграла

1. Интеграл от алгебраической суммы функций равен

При

алгебра ческой сумме

нтегралов от всех слагаемых:

b

b

b

f x g x dx f x dx g x dx.

a

a

a

a

2.

бАa

перестановке пределов интегрирования меняется знак

интеграла:

b

a

f x dx f x dx.

a

b

3.Интеграл с одинаковыми пределами равен нулю:

b

f x dx 0.

b

b

b

4. Если f x g x при всех x a;b , то f x dx g x dx.

5.Если m f x M при всех x

из промежутка a;b , то

b

m b a f x dx M b a .

a

И

6. Отрезок интегрирования Дможно разбивать на части:

b

c

b

f x dx f x dx f x dx, с a,b .

a

a

c

Данное свойство называется свойством аддитивности.

7. Постоянный множитель можно выносить за знак интеграла:

b

b

kf x dx k f x dx (k постоянная).

a

a

8.

Теорема (о

среднем значении). Пусть функция y f x

непрерывна x a,b .

Тогда существует точка c a,b

такая, что

f x 0

x a, b ).

Значен е f c

называется

средним

значением

функции

на

отрезке:

наи

1

С fcp

b

f x dx.

a

b a

Доказательство.

Так

как

функция

y f x

непрерывна

на

отрезке, то, по второй теореме

Вейерштрасса, f x

достигает

на

отрезке a, b своего

ольшего M и наименьшего m значения:

m f x M всюду на отрезке (рис. 3.2).

Проинтегрируем это неравенство на отрезке a, b :

b

b

b

m dx f x dx M dx.

a

a

a

Д

ПолучимбА

b

1

b

m b a f x dx M b a m

f x M .

b a

a

И

a

b

1

b

m b a f x dx M b a

m

f x M , так как

a

b a a