3.3. Методы вычисления определенного интеграла

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1889.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

2.09 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1610 11 12 13 14 15 16 > Следующая >>>

4						x			4						4	x									x			4
4						x			4						4	x									x			4
(1 e4 )dx dx 4 e4d																		x	(x 4e4 )										4 4e 4 4e.
(1 e4 )dx dx 4 e4d																			(x 4e4 )										4 4e 4 4e.
0									0						0	4												0
																1								1				0
																1										2x ln2)dx.
Пример 5. Вычислить (3x2
Пример 5. Вычислить (3x2
																0							x2 1
Решение. Разложим определенный интеграл на сумму трёх
табличных интегралов и получим следующее:
1				2	1							x								1		2				1			dx				1		x
(3x										2				ln2)dx 3 x										dx						ln2 2						dx
(3x							x2			2				ln2)dx 3 x										dx						ln2 2						dx
0							x2	1												0						0 x2 1							0
(x			3		arctgx								x		1														1			0					.
			3										x		1														1			0
											2			)	1 arctg1 arctg0 2																2
											2			)	1 arctg1 arctg0 2																2
С															0																			4
С															0																			4

Пр мер 6. Выч																4
Пр мер 6. Выч																	sin4xdx.
																0
Решен е. Прео разуем выражение под знаком дифференциала и
слить																											и		формулой								Ньютона –
воспользуемся								та л цей									интегралов										и		формулой								Ньютона –
Лейбн ца:

	4							1 4												1						4			1							1
	sin4xdx										sin4xd					4x					cos4x										(cos cos0)							.
	sin4xdx										sin4xd					4x					cos4x										(cos cos0)							.
0								4			0									4						0			4							4
0								4			0									4						0			4							4
					3.3. Методы вычисления определенного интеграла
ПриёмыбвычисленияАопределенных интегралов практически
ничем		не				отличаются									от		всех			тех приемов											и	методов, которые

применяются при нахождении неопределенных интегралов.

Точно так же применяются методы подстановки (замены

переменной), метод интегрирования		по	частям, те же приемы
нахождения	Д
нахождения	первообразных	для	тригонометрических,
			И

иррациональных и трансцендентных функций. Особенностью является только то, что при применении этих приемов надо распространять преобразование не только на подынтегральную функцию, но и на пределы интегрирования. Заменяя переменную интегрирования, надо не забыть изменить соответственно пределы интегрирования.

3.3.1 .Замена переменной в определенном интеграле

Теорема (о замене переменной в определенном интеграле). Пусть функция y f x непрерывна x a,b и x x t . При этом

1) x a,

x b;

2) x t , x t

непрерывны t , .

Тогда формула замены переменной в определенном интеграле

имеет в д f (x)dx

f (x(t))x (t)dt.

F x

Доказательство.

–

первообразная

для

функции

f (x), то, по формуле Ньютона –

∫f (x)

dx F b F a .

Если

первообразная

для

функции

Функц я

F x

t ,

очевидно,

f x t x t , поэтому

Лейбница

F x

F a .

f x t x

t dt

F x

Таким образом, левая и правая части формулы равны, что и

требовалось доказать.

ln2

Пример 1.

Вычислить

1 ex

dx.

Решение. Сделаем замену переменной по формуле t

1 ex

. Тогда

1 x ln t

t2 1

Кроме того,

если

x 0,

то

;

если

x ln2,

то t

Следовательно,

ln2																	3					2t dt													3 t2 1 1																				3											3		dt
							x										3					2t dt													3 t2 1 1																				3											3		dt
		1 e							dx												t							2																			dt 2													dt
		1 e							dx												t							2																			dt 2													dt
																						t2 1																t2		1																												t2 1
																			2			t2 1													2			t2		1																		2									2	t2 1
0																			2																2																							2									2

																	1							t 1								3																																	3 1						2 1
																																3
2			3								2									ln														2									3								2		ln																				.
2			3								2									ln														2									3								2		ln																				.
																	2							t 1																																									3 1						2 1

																																2


Замечан е. Следует обратить внимание на то, что при
выполнен							замены																переменной																			в определенном																										интеграле надо
изменяется
пересч тать пределы																								нтегрирования, т. е. найти отрезок, на котором
Сновая переменная, но при этом к старой переменной
возвращаться не надо.
			бА
																				3.3.2. Интегрирование по частям
Формула															нтегр рования																									по									частям														для						определённого
интеграла					меет в												д												b																							b
																													u dv u v\|ba v du.
																													a	1																						a
																														1
Пример 2. Вычислить xarctgxdx.
																														0								Д
Решение. Положим u arctgx;																																													dv xdx. Следовательно,
																																												1																									x2
													du arctgx dx																																					dx,v												xdx								.
													du arctgx dx																																			2		dx,v												xdx								.
																																								1 x																												2
Тогда по формуле интегрирования по частям имеем
1																					x		2										1					1	x		2								1
xarctgx dx																					x				arctgx								1						x										1					dx
																																	\|
																					2												\|							2
0																					2												0					0		2						1 x2
	1	arctg1										02						arctg0												11							x2							dx								1										11 x2 1 1										dx

	2											2																		2						1 x2																										2					x2 1
	2											2																		2			0			1 x2																2 4										2		0			x2 1
			1				1			x		2			1												1																				1		1											1
																															dx																		1																	Иdx
												2														2					dx																		1																	Иdx
												2			1										x	2	1													8 20																1 x								2
	8 20 x														1										x		1													8 20																1 x
				1		x		\|1						1		arctg x\|1																					1								0														1		.
						x		\|1								arctg x\|1																													0																.
	8		2					0				2															0				8					2					8											4					2
																															4
Пример 3. Вычислить x																																					x2			9dx.
																														0

Решение.														Сделаем												замену												t x2 9, тогда																				dt d x2 9 ;
dt 2xdx;						dx								dt	.		Новые													пределы											интегрирования																		находим из
dt 2xdx;						dx								2x	.		Новые													пределы											интегрирования																		находим из
														2x																																										02
соотношения											t x2 9.											Поэтому если																				x 0,								то t						02		9 9, если
С1																	3																																				1
С1																	3
x 4, то t2					42								9 25и получаем																																												1
												4																25									dt				125												1 25


												x			x2 9dx x t																																t dt									t2dt
												x			x2 9dx x t																					2x											t dt									t2dt
							1					0							3									9								2x					2 9												2 9
							1		1										3																		3				3
	1 t					2			1			\|25				1		t	2		\|25										1														1									3					3
						2													2																																			3					3
																																25					2 92															25 9
																																25					2 92															25 9
2												9			2							9								3															3
								1
				2				1									2
				2													2			53
																	1						33										1	125 27												98					.
																							33											125 27																	.
					бА
																	3															3													3
и2sin xdx
Пр мер 4.														Выч слить																									2 .
																														1 cosx
																									2
Решение. Введём новую переменную,																																													полагая 1 cosx t,																	тогда
																																											dt
dt 1 cosx dx;																	dt sin xdx;																					dx											.				Новые								пределы
dt 1 cosx dx;																	dt sin xdx;																					dx					sin x						.				Новые								пределы
интегрирования находим из соотношения																																													t 1 cosx.													Подставим в
него x			,							получим t												1 cos													1 0 1,														если						x ,					то верхний
него x			,							получим t												1 cos													1 0 1,														если						x ,					то верхний
		2																		1												2
предел интегрирования t2 1 cos 1 ( 1) 2.
В результате преобразований получаем																																													И
																									7			dt																	И
			2sin xdx														2 2sinx																				2 dt				2													t 2 1				2			t 1	2
																											sinx Д
																																	2						2 2 t					2				dt 2										\|1		2		\|1
		1 cosx															1							t													1 t				1													2 1							1
2										1														1
										1														1
2												1			2														1.
2										2		1			2														1.
										2														2
Пример 5. Вычислить																																	dx							.


																									0				3 (8 x)2
Решение.														Сделаем													замену												переменной:																	8 x t ,						тогда
					dx dx.												Отсюда следует, что dx dt. Новые пределы
dt 8 x					dx dx.												Отсюда следует, что dx dt. Новые пределы

интегрирования находим из соотношения t 8 x. Подставляя в него значение x 0, получим t1 8 0 8; если же x 7, то t2 8 7 1.

Таким образом, в результате подстановки получим простой табличный интеграл

												8
												8
	dx			dt			2		t		1
7		1			8		2				3			8
			(			) t	3dt						33 t


0 3 (8 x)2		8		3 t2	1					1				1
0 3 (8 x)2		8		3 t2	1					1				1
								3				1
								3				1

слить				x 2
3(3	8 3	1) 3(2 1) 3.
СПр мер 6. Выч			e
СПр мер 6. Выч			xln xdx.
		1

Решен е.					Пр меним								формулу							интегрирования								по частям.
			бА																										x2
																								1					x2
Полож м			u ln x;				dv xdx, тогдаdu ln x dx																		dx;v			xdx		.
Следовательно,
e							2				e		x	2			1			e	2		2			1	e
xln x dx x								ln x\|e				2						dx		2		lne		ln1			xdx
1						2			1		1	2					x			2			2		2		1
1	e	2	1 1		x	2	e	1	e	2		1			e	2			1 e2			1	.
							\|
							\|					4							4		4
2			2	2			1	2				4							4		4

Пример 7. Вычислить 2x 5 cos2x dx.

Решение. Данный интеграл вычислим с помощью формулы интегрирования по частям.

								u 2x 5					du 2dx						И
2x 5 cos2x dx																			И
2x 5 cos2x dx															sin2x
0								dv cos2Дx dx v
															2
	2x 5											cos2x				1	cos2 cos0 0.

			sin2x			sin2x dx 0
		2	sin2x			sin2x dx 0									2
					0	0							2	0
					0	0							2	0
				Задачи для самостоятельного решения
Вычислить определенные интегралы:
3		dx				2	2		1		1		dx		2				dx
1.				. 2.		(x				)dx. 3.						. 4.				.
1.		3x 2		. 2.		(x			x4	)dx. 3.			(2x 1)3			. 4.		x2 5x 4		.
1		3x 2				1			x4		0		(2x 1)3		1			x2 5x 4

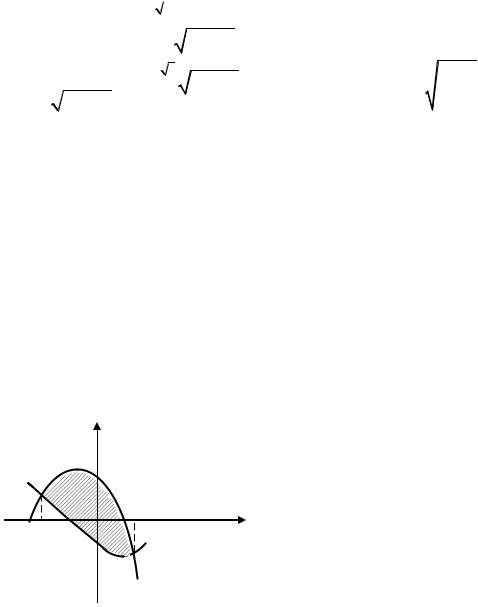
5. (x 3)dx. 6.															xdx
																			. 7.												ln(x 1)dx.
																			. 7.				sin xcos2 xdx. 8)								ln(x 1)dx.
2										3												2									1
		x2 4
0		x2 4								0				4 x2								0									0
			xdx																							dx
5																						3								0.5			x
											2
											2							2
9)						. 10.									2 x				dx. 11.									,		12.					dx.
																									x x2							1 x
			4x 5
1			4x 5							1												1								0
																				Ответы
1.	ln13			. 2.	21			. 3.				2	. 4.			1	ln			5	. 5.			3			ln2		. 6. 1.		7.		1	. 8. 2ln2 1.
1.				. 2.				. 3.				2	. 4.			1	ln			5	. 5.			3			ln2		. 6. 1.		7.		1	. 8. 2ln2 1.
и																			4			8			2						3
3					8					9			3						4			8			2						3
С17 2													3									2
9.			. 10.		4				. 11. ln								.		12.			4			.
6					4								2									4
3.4. Пр ложен я определенного интеграла (видео 1, видео 2)
				3.4.1. Выч сление площади плоской фигуры
				y																					Если y1 x y2 x											x a, b , то,
				y																				исходя						из			геометрического
																								исходя						из			геометрического
						y y2				x														смысла определённого интеграла,
																								площадь						области,						ограниченной
							b													Д																	функций
а			0																	x
			бА(рис.3.5), можно вычислить по
y y1 x																								формуле
																														b
				Рис. 3.5																							S y2 x y1 x dx.
				Рис. 3.5																										a

Пример 1. Вычислить площадь области, ограниченной линиями y 4 x2 и y 3x.

Решение. Построим графики этих функций (рис. 3.6) и найдем
точки их пересечения:	И
4 x2 3x x2 3x 4 0 x 1, x 4.
	1	2

	y			Искомую площадь фигуры найдём
	4			по формуле, приведённой выше:
y 3x	4	4 x2
y 3x		4 x2
С				4																3			2	4
				4																3			2	4

		4	x	S 4 x2 3x dx 4x x 3x
-1		4	x	S 4 x2 3x dx 4x x 3x
				1															3			2		1
				1																				1
Если				16	64			24 4			1			3			125				.
				16				24 4													.
				3						3			2					6
				3						3			2					6
Р с. 3.6
	бА
	функц я задана параметрически:
	x x(t);		x t	a; y t b; y t 0 t t ,t															2	,
													1						2
	y y(t),
то площадь криволинейной трапеции, ограниченной ее графиком и
отрезком [a,b] оси Ox, вычисляется так:
			b		t2
		S y x dx y t x t dt .
			a		t1
Пример 2. Вычислить площадь фигуры, ограниченной линиями
			y sin x; y 2 sin x;							x					5	;			x 0.
			y sin x; y 2 sin x;							x						;			x 0.
													4
				Решение. Искомая площадь S равна
									И
			сумме площадей S1									и			S2			двух				фигур,
			перваяДиз которых ограничена линиями
			y sin x; y 2sin x;								x 0;							x ,				вторая
			ограничена линиями											y sinx;y 2sin x;
			x ; x			5	(рис. 3.7).
			x ; x				(рис. 3.7).
				4
				Вычислим отдельно площади фигур
			S1	и S2:

Рис. 3.7


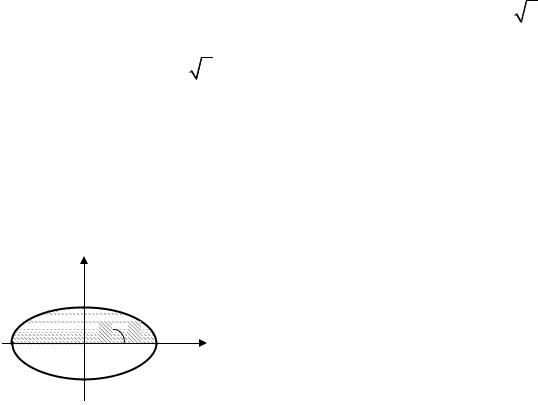
S1	2sin x sin x dx sin xdx cosx \| cos cos0
0	0	0
1 1 1 1 2.

фигуры,

лежащей

четвёртой

четверти,

Площадь

sin x 2sin x dx sin xdx cosx | cos

cos 1

Тогда S S

2,293.

Пр мер 3. Выч

площадь эллипса

1 (рис . 3.8).

бА

слить

Решение.

Запишем

уравнение

эллипса в параметрическом виде

x acost;

y bsint.

Значению

x a

соответствует

-a

t1 ; если x a, то t2

Рис.3.8

Следовательно,

y x

Д1 cos2t ab

dx b sint a sint dt

2 a

Поэтому площадь эллипса находится по формуле S ab.

3.4.2. Вычисление объёма телаИвращения

Покажем, что если S x

– площадь сечения пространственного

тела плоскостью x const, то его объем будет равен V S x dx,

где

x a – абсцисса крайней левой точки,		а x b – абсцисса крайней
правой точки тела.
Разобьем	тело плоскостями	x xi, i 0,1,...,n	на	n
произвольных	достаточно тонких слоев. На рис. 3.9		показан	i-й
			n

слой, объем которого обозначим Vi . Тогда объём всего тела V Vi .

i 1

и
С… xi 1	…	x
бА
Рис. 3.9

Так как слои достаточно тонкие, то можно считать, что их объем приблизительно равен о ъему цилиндра с высотой h xi xi 1 xi и


площадью основания S	x	,	где x x ,			x	– произвольная точка,
	i			i	i 1	i
n			Д
i 1,..., n. Значит, V S xi			Д
i 1,..., n. Значит, V S xi			xi .

i 1

Полученная сумма является n-й интегральной суммой для функции S x на отрезке a, b , поэтому ее предел при n , d 0,

если он существует и не зависит от способа составления суммы, равен определенному интегралу, т. е. И

V S x dx.

Рассмотрим тело, образованное вращением вокруг оси Ox криволинейной трапеции, ограниченной графиком функции y y(x), осью Ox и прямыми, уравнения которых x a и x b(рис. 3.10).

	Любое сечение плоскостью	x const
у	образованного таким образом тела
у	вращения – круг радиусом	r y x ,

				площадь которого
					S x r2 y2 x .
а	О	х	b	х Тогда , применяя общую формулу для
С				вычисления объёма, получим
						b
					Vx y2 x dx.
						a
Р с. 3.10
Индекс	x	в	формуле	указывает	на то,	что	тело получено
и
вращен ем кр вол нейной трапеции вокруг оси OX .
Пр мер 4.			Выч слить	о ъём тела, полученного вращением
			x t sint;
одной арки циклоиды				вокруг оси OX (рис. 3.11).
			y 1 cost
Решение. Одной арке циклоиды соответствует изменение
переменной	x		и параметра t на		промежутке		0, 2 , поэтому
dx 1 cos t	dt,; y 1 cos t и
бА
у					2
					Vx y2 x dx
					0
					2
				Д
					1 cost 2 1 cost dt.
					0
О				х	При	вычислении		этого
О			2		При	вычислении		этого
					интеграла		воспользуемся
	Рис.3.11				формуламиИ:
	Рис.3.11

1 cost 3 dt 1 3cost 3cos2 t cos3 t dt

1 cos2t

1 3

dt 5

3.4.3. Выч слен е площади поверхности тела вращения

поверхности

малых

частей

точками

Пусть

кр вая

y y x ,

x a,b

вращается

вокруг

оси

OX .

Выведем формулу для вычисления площади получающейся таким

образом

вращения (рис.3.12).

Будем сч тать, что функция

y y x

дифференцируема на

бА

отрезке a,b . Разо ьем отрезок a, b

на n

произвольных достаточно

x xi,

i 0,1,...,n

впишем

кривую

ломаную

со

Mi 1

y y x

звеньями

Mi 1

Mi,

i 1,...,n.

Каждое

звено

этой

ломаной

О … xi 1

…

описывает

при

вращении

поверхность

усеченного конуса

площадь

которой

вычисляется

по

известной

Рис.

формуле S (r1 r2) l.

Рис. 3.12

3.12

Поэтому

Si y xi 1 y xi i ,

где

–

длина отрезка

Mi 1Mi (образующая конуса).

По теореме Пифагора,

x x

y y

x yИx 1 ,

i 1

а по теореме Лагранжа,

yi 1

y ci ,

где

xi 1,xi

xi 1

Следовательно,

1 y 2 ci xi

Si y xi 1 y xi 1 y 2 ci xi .

Тогда площадь поверхности вращения

S Si y xi 1 y xi

1 y 2 ci xi .

i 1

Если существует не зависящий от способа составления

полученной суммы её предел при n , d 0

– наибольший из

диаметров разб ен я),

то в результате предельного перехода в этом

слить

равенстве получ

м, что

S 2 y x

1 y x dx.

бА

Эта формула остается неизменной при любом способе задания

функц y y x .

Пр мер 5. Выч

площадь поверхности тора, полученного

вращен ем окружности

x2 y b 2

a2,

вокруг оси

(рис. 3.13).

Решение.

Площадь

поверхности

тора

равна

сумме

площадей

поверхностей,

полученных

при

вращении

верхней

половины

окружности

ее

y b a

нижней половины y b

-a

a2 x2

Чтобы

воспользоваться

формулой, найдем производные

Рис. 3.13

y x

a2 x2

2 a2 x2

1 y

1 a2 x2 a2 x2

a2 x2

b a2 x2

S Sв Sн 2 2

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1610 11 12 13 14 15 16 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.20212.07 Mб51884.pdf
#
07.01.20212.08 Mб141885.pdf
#
07.01.20212.08 Mб31886.pdf
#
07.01.20212.08 Mб151887.pdf
#
07.01.20212.09 Mб131888.pdf
#
07.01.20212.09 Mб311889.pdf
#
07.01.2021336.18 Кб17189.pdf
#
07.01.20212.09 Mб201890.pdf
#
07.01.20212.1 Mб471891.pdf
#
07.01.20212.1 Mб211892.pdf
#
07.01.20212.11 Mб131893.pdf