
- •ВВЕДЕНИЕ
- •Раздел 1. МАТЕМАТИЧЕСКИЙ АНАЛИЗ
- •1. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- •1.1. Определение и основные понятия
- •1.3. Элементы скалярного поля
- •1.4. Локальный экстремум функции двух переменных
- •1.5. Метод наименьших квадратов
- •2. НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
- •2.1. Первообразная функция и неопределенный интеграл
- •2.2. Замена переменной в неопределенном интеграле
- •2.3. Интегрирование по частям
- •2.4. Интегрирование рациональных дробей
- •2.4.3. Интегрирование неправильных рациональных дробей
- •3. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
- •3.1. Определенный интеграл, его свойства
- •3.2. Формула Ньютона – Лейбница
- •3.3. Методы вычисления определенного интеграла
- •3.3.1 .Замена переменной в определенном интеграле
- •3.4.4. Длина дуги плоской кривой
- •3.5. Несобственные интегралы
- •4. КОМПЛЕКСНЫЕ ЧИСЛА
- •Комплексные числа и действия над ними
- •5.1. Основные понятия
- •5.2. Дифференциальные уравнения первого порядка
- •6. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА

10. Найти производную функции u ln(ex ey) в направлении биссектрисы первого координатного угла.
11. Найти градиент и его модуль функции u x2 2x
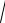 y y3z в
y y3z в
точке M(1;1;3).
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
2 |
|
|
|
5 |
|
|
|
|
|
||||||||||||||
12. Найти модуль градиента функции u |
y2 |
z2 . |
|
|
|
|
||||||||||||||||||||||||||||||||||||||
и |
|
|
|
Ответы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
12 |
|
|
|
|
|
||||||||||||||||
1. x2 |
2y |
3 |
парабола. |
2. 3. |
3. |
|
gradz(M) |
|
|
. 4. |
|
0. 5. |
. |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
5 4 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||||
6. |
|
2 |
|
. |
7. |
|
. |
8. ( 3;1) и |
|
(1; 1). |
9. 2 |
|
|
|
. 10. |
|
2 |
|||||||||||||||||||||||||||
|
|
|
3 |
|
||||||||||||||||||||||||||||||||||||||||
2 |
бА |
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
11. gradu(M) (4; 8; 1); |
gradu(M) |
3; 12. |
gradu |
1. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
1.4. Локальный экстремум функции двух переменных |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
Говорят, что функция z f (x, y) |
имеет максимум (минимум) в |
|||||||||||||||||||||||||||||||||||||||||||
точке M0(x0,y0), если |
f (x0, y0 ) f (x, y) (или |
f (x0, y0 ) f (x, y)) для |
||||||||||||||||||||||||||||||||||||||||||
всех точек (x, y), достаточно |
лизких к точке(x0, y0) |
и отличных от |
||||||||||||||||||||||||||||||||||||||||||
неё. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Максимум и минимум функции называются локальными |
||||||||||||||||||||||||||||||||||||||||||||
экстремумами функции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Теорема. (Необходимые условия существования экстремума |
||||||||||||||||||||||||||||||||||||||||||||
функции двух переменных). Если функция z f (x, y) |
имеет в точке |
|||||||||||||||||||||||||||||||||||||||||||
M0(x0,y0) локальный экстремумДи частные производные первого |
||||||||||||||||||||||||||||||||||||||||||||
порядка, |
то |
все |
эти |
частные |
производные |
|
равны |
|
нулю |
при |
||||||||||||||||||||||||||||||||||
x x0;y y0, т. е. |
f |
|
|
|
0; |
f |
|
|
|
0. |
|
|
|
Иf |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
x |
M0 |
y |
M0 |
|
f |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Точки, в которых одновременно |
|
|
0 |
и |
|
|
|
0, |
|
называются |
||||||||||||||||||||||||||||||||||
|
x |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
||||
стационарными.
Данная теорема не является достаточной для исследования вопроса о существовании локального экстремума функции в стационарных точках.
20

Теорема. (Достаточные условия существования экстремума функции двух переменных).
Пусть в некоторой области, содержащей точку M0(x0,y0),
функция |
z f (x, y) |
имеет непрерывные частные производные до |
||||||||||||||||||||||||||||||||||||||
третьего порядка включительно; пусть, кроме того, в этой точке |
||||||||||||||||||||||||||||||||||||||||
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
f (x0, y0) |
0 |
и |
|
f (x0, y0) |
0. Тогда при значениях x x0, y y0 |
|
|
||||||||||||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1) функц |
я |
|
|
меет экстремум в стационарной точке, |
если число |
|||||||||||||||||||||||||||||||||
|
|
A B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B C |
|
|
|
|
|
|
|
|
||||||
|
причём |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
B C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x ,y |
|
) z |
|
|
приA 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
0 |
|
|
0 |
|
|
|
|
max |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
f (x0,y0) zmin приA 0; |
|
|
|
|
|
|
|
A B |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
2) функц я не |
меет экстремума, если число |
0; |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
3) если ч сло |
A B |
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
B C |
0, то экстремум функции может быть, а |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
б |
||||||||||||||||||||||||||||||||||||||
может |
и |
не ыть (в этом случае требуется дополнительное |
||||||||||||||||||||||||||||||||||||||
исследование), |
|
где |
о означили через A, |
|
B |
и |
|
C соответственно |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 f |
|
|
2 |
|
f |
|
2 f |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
значения частных производных второго порядка |
|
|
|
|
|
, |
|
|
|
|
|
|
и |
|
|
|
|
|||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
x y |
|
y |
|
||||||||
в стационарной точке M0(x0,y0). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
Пример 1. Найти экстремум функции z x3 |
8y3 |
6xy 5. |
|
|
||||||||||||||||||||||||||||||||||
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||||||||||||||||||||||||
|
|
|
Находим частные производные первого порядка zx , |
|||||||||||||||||||||||||||||||||||||
|
zy и точки, в которых они равныДнулю или не существуют и которые |
|||||||||||||||||||||||||||||||||||||||
лежат |
|
внутри |
|
|
|
области |
определения |
функции: |
|
|
|
zx |
3x2 |
6y; |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
zy 24y2 6x. |
Решая систему уравнений |
|
x |
|
|
|
найдём две точки |
||||||||||||||||||||||||||||||||
|
|
|
0, |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
zy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M1(0;0) |
|
|
|
M2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
и |
1; |
|
. |
Обе |
точки |
являются стационарными. |
Далее |
||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
исследуем |
эти |
|
|
точки по |
знаку |
определителя |
|
|
|
|
|
A B |
|
. Найдём |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
B C |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
частные производные второго порядка и обозначим: zxx A 6x;
21

|
|
|
|
|
|
Далее |
вычисляем |
|
их |
значения в |
||||||
zxy B 6; |
zyy C 48y. |
|
||||||||||||||
стационарных точках. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Для |
точки |
|
M1 |
получим |
A 0; |
|
B 6; |
|
C 0 |
и |
||||||
(M1) AC B2 36 0. |
Следовательно, |
|
в |
|
точке |
M1 |
нет |
|||||||||
экстремума. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для точки M2 |
имеем A 6; |
B 6; C 24 |
и (M2) 108 0. |
|||||||||||||
огласно достаточному условию существования экстремума, M2 |
есть |
|||||||||||||||
точка м н мума. zmin |
z(M2) 4. |
|
|
3 |
|
|
|
|
|
|
||||||
точки2 |
|
|
на |
|
|
|
|
функцию |
||||||||
Пр мер |
2. |
|
Исследовать |
экстремум |
|
|||||||||||
3 |
2 |
|
5 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
Сz x y 3x 4 y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решен е. |
Найдём о ласть определения данной функции. Это |
|||||||||||||||
все |
бА |
|
|
|
|
|||||||||||
M(x, y), |
|
координаты |
которых удовлетворяют системе |
|||||||||||||
неравенств x ; 0 y . |
Найдём частные |
производные |
||||||||||||||
первого |
порядка |
z |
3 |
; |
z |
2y 2 |
|
y . |
|
Решая |
систему |
|||||
|
3x |
y |
|
|
||||||||||||
|
z |
|
x |
|
|
|
|
|
|
|
|
|
|
|
||
|
0, |
|
|
|
|
|
M1(1;0) и M2 1;0 , которые |
|||||||||
уравнений x |
найдём две точки |
|||||||||||||||
|
zy |
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
лежат не внутри о ласти определения функции, а на её границе y 0. |
||||||||||||||||
Поэтому |
точки M1 |
|
и M2 не |
являются стационарными |
и данная |
|||||||||||
функция не имеет экстремума. |
Д |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
1.5. Метод наименьших квадратов |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
И |
||||||||
Метод наименьших квадратов является непосредственным результатом применения исследования на экстремум функции двух переменных и заключается в следующем. На плоскости Oxy имеется система точек (xi , yi ), где i 1,...,n. Требуется подобрать некоторую функцию y f (x), которая «сглаживала» бы все точки этой системы, т.е. величина квадрата отклонения ординаты функции f в точке xi от ординаты yi данной точки была бы минимальной:
n
2( f ) (yi f (xi ))2 0.
i 1
Полученная формула y f (x) называется эмпирической.
22

При обработке опытных данных наиболее распространённым является приближение эмпирической формулой в виде линейной функции одной переменной. В этом случае эмпирическая формула имеет вид f (x) ax b.
Коэффициенты a и b «сглаживающей» прямой находятся из системы двух линейных уравнений с двумя неизвестными :
|
|
|
|
n |
|
|
n |
|
n |
|
|
|
|
; |
|
|
|
|
a x2 |
b x x y |
|
||||||||||
|
|
|
|
i 1 |
i |
|
i |
|
|
|
i |
i |
|
|
|
|
|
|
|
|
i 1 |
|
i 1 |
|
|
|
|||||
|
|
|
|
n |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
a x b n y . |
|
|
|
|||||||||
и |
i |
|
|
|
|
i |
|
|
|
|
|
||||
|
|
|
|
i 1 |
|
|
i 1 |
|
|
|
|
|
|
||
СПр мер. Имеются данные наблюдений |
|
|
|
|
|
|
|||||||||
|
x |
|
17.0 |
17.3 |
|
18.3 |
18.5 |
|
18.8 |
|
19.2 |
|
|||
|
бАi |
|
|
|
|||||||||||
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
i |
534 |
537 |
|
550 |
552 |
|
555 |
|
560 |
|
|||
Предполагая, что между переменными x и y существует |
|||||||||||||||
линейная зависимость, найти |
эмпирическую |
формулу y ax b |
|||||||||||||
методом наименьших квадратов.
Решение. Для вычисления необходимых сумм заполним вспомогательную та лицу
|
|
|
|
|
|
|
|
|
|||
|
i |
x |
y |
|
|
Д |
|||||
|
|
i |
|
i |
|
|
x |
|
i |
i |
|
|
1 |
17.0 |
534 |
|
|
289 |
9078 |
|
|
||
|
2 |
17.3 |
537 |
|
|
299.29 |
9290.1 |
И |
|||
|
3 |
18.3 |
550 |
|
|
334.89 |
10065 |
||||
|
4 |
18.5 |
552 |
|
|
342.25 |
10212 |
||||
|
|
|
|
||||||||
|
5 |
18.8 |
555 |
|
|
353.44 |
10434 |
|
|||
|
6 |
19.2 |
560 |
|
|
368.64 |
10752 |
|
|||
|
|
109.1 |
3288 |
|
|
1987.51 |
59831.1 |
|
|||
Составим систему уравнений для нахождения неизвестных |
|||||||||||
коэффициентов a и b эмпирической функции |
|
|
|||||||||
|
|
1987,51a 109,1b 59831,1; |
|||||||||
|
|
109,1a |
|
|
6b 3288. |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
Решая эту систему любым способом, находим a и b: a 11,946; b 330,78.
Искомая эмпирическая формула будет y 11,946x 330,78.
23

Задачи для самостоятельного решения
Исследовать на локальный максимум и минимум функции:
|
1. |
z x2 y2 xy 9x 6y 20. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
2. |
z 3x 6y x2 xy y2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
3. |
z x |
|
|
x2 y 6x 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
4. |
z x3 y2(6 x y). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
5. |
z x2 |
xy y2 |
|
1 |
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Найти |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
3 |
|
|
3 |
3xy. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
С6. z x y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
7. |
z (x2 y) ey . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
8. |
|
|
бА |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
стац онарные точки функции |
z x3 y2 4xy 3x2. |
|
|
||||||||||||||||||||||||||||||
|
9. |
В результате эксперимента для пяти значений аргумента x |
||||||||||||||||||||||||||||||||||||
получены пять значен й величины y: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
xi |
|
|
|
|
-2 |
|
|
0 |
|
1 |
|
|
2 |
|
|
4 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
yi |
|
|
0.5 |
|
|
1 |
|
1.5 |
|
|
2 |
|
|
3 |
|
|
|
|
|
|
|
||||||||||
|
Методом наименьших квадратов найти эмпирическую формулу |
|||||||||||||||||||||||||||||||||||||
y ax b. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1. zmin z( 4;1) 1. 2. zmin z(0;3) 9. 3. zmax z(4;4) 15. |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
9 |
|
|
|||||||
|
4. |
|
|
|
|
z |
max |
z(3;2) 108. Д5. z z( |
|
|
; |
|
|
|
) |
|
|
|
|
. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
min |
3 3 |
3 3 |
|
|
|
3 9 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||
6. zmin z(1;1) 1. 7. |
zmin |
z(0; 2) |
. |
8. Стационарная точка |
||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
И |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
M0 |
|
, |
|
. 9. |
y 0.425x 1.175. |
|
|
|||||||||||||||||||||||||||||||
3 |
3 |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
24

|
|
Вопросы и задания для самопроверки [1,2,3] |
|
|||||
1. |
формулируйте понятие функции нескольких переменных. |
|||||||
2. |
Какие способы задания функции двух переменных вы знаете? |
|||||||
3. |
|
формулируйте определение предела функции двух |
||||||
С |
|
|
|
|
|
|
||
переменных. |
|
|
|
|
|
|
||
4. |
Какая |
функция |
|
нескольких |
переменных называется |
|||
непрерывной? |
|
|
|
|
|
|
||
5. |
Как определяются частные и полное приращения функции |
|||||||
нормали |
|
|
|
|
||||
двух переменных в точке? |
|
|
|
|
|
|||
6. |
Дайте определения частных производных первого порядка. |
|||||||
7.Как |
зап сываются |
уравнения касательной плоскости и |
||||||
|
к поверхности? |
|
|
|
|
|
||
8. |
бА |
|
|
|||||
Как определяются частные производные высших порядков? |
||||||||
9. |
Сформул руйте понятие полного дифференциала функции |
|||||||
нескольк х |
переменных |
|
и укажите |
его |
применение |
для |
||
прибл женных выч слений. |
|
|
|
|
|
|||
10. Дайте определение скалярного поля, линий уровня, |
||||||||
поверхностей уровня. |
|
|
|
|
|
|||
11. Что называется производной по направлению? |
|
|||||||
12. Определите, что такое градиент и укажите его свойства. |
|
|||||||
13. Какая |
точка называется локальным |
максимумом |
или |
|||||
минимумом функции двух переменных?
14.Сформулируйте необходимые и достаточные условия существования локальных экстремумов функции в точке.
15. В чём состоит суть метода наименьших квадратов?
|
|
|
|
И |
||||
|
|
Контрольная работа по разделу «Функции нескольких |
||||||
|
|
|
переменныхД» |
|||||
|
|
|
Вариант 1 |
|
|
|
|
|
1. |
Найти область определения функции z |
x2 4 |
y2 |
4. |
||||
2. |
Найти частные производные первого |
порядка |
функции |
|||||
z |
5x2 2y |
. |
|
|
|
|
|
|
3x y2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
3. |
Найти градиент функции z 3x2 y 3xy2 y3 в точке M(1;2). |
|||||||
25
|
4. |
|
|
Составить уравнение касательной плоскости к поверхности |
|||||||||||||||||||||||||
z y3 |
|
x2 y в точке A(3;4). |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
5. |
|
|
Найти |
|
частные |
производные |
второго |
порядка |
функции |
|||||||||||||||||||
z xy |
2 |
x |
3 |
|
1 |
|
y |
4 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. |
|
Исследовать на экстремум функцию z x2 |
2xy 4x y2. |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 2 |
|
|
|
|
|
|
|
|
|
|
|
Найти |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
y sin x . |
|
||||||||||||||||||||||||
|
1. |
|
Найти область определения функции z |
|
|||||||||||||||||||||||||
|
2. |
|
|
|
|
|
|
|
|
|
|
|
|
частные |
производные |
первого |
порядка |
функции |
|||||||||||
z |
2x |
|
x |
2 |
y |
3 |
ln y. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
y |
|
|
|
|
|
|
бА |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
3. |
|
|
|
|
|
|
|
|
|
град ент функции z 2 |
x2 |
3y в точкеM( 1;1). |
||||||||||||||||
|
4. |
|
|
Состав ть уравнение касательной плоскости к поверхности |
|||||||||||||||||||||||||
z x2 |
|
y2x в точке M(2; 1). |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. |
|
|
Найти |
|
частные |
производные |
второго |
порядка |
функции |
|||||||||||||||||||
|
|
|
|
|
|
Д |
|||||||||||||||||||||||
z |
|
xy 1 |
x3y. |
|
|
||||||||||||||||||||||||
|
6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
Исследовать на экстремум функцию z x2 |
xy y2 x y 1. |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
z x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Найти градиент функции z 2x2 xy3 в точке M(1;2). |
|
|||||||||||||||||||||||||||
|
3. |
|
|
||||||||||||||||||||||||||
|
4. |
|
|
Составить уравнение касательной плоскостиИк поверхности |
|||||||||||||||||||||||||
z xy2 2 |
|
|
|
x |
в точке M(1; 1). |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
5. |
|
|
Найти |
|
частные |
производные |
второго |
порядка |
функции |
|||||||||||||||||||
z (
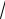 x y)2.
x y)2.
6. Исследовать на экстремум функцию z x2 y2 12x 16y.
26
|
Вариант 4 |
|
|
|
|
1. |
Найти область определения данной функции z x |
|
|
. |
|
|
y 1 |
||||
2. |
Найти частные производные функции z x3y 2y3. |
|
|
|
|
С |
в точке M |
2; 1 . |
|||
3. |
Найти градиент функции z x2 xy 2y2 |
||||
4. |
оставить уравнения касательной плоскости к поверхности |
||||
z x2 |
2xy2 5y в точке 1; 1 . |
|
|
|
|
5. |
Найти частные производные второго |
порядка |
|
функции |
|
z(x2 y2)x y3.
6.Исследовать на экстремум функцию z x2 y2 xy 4x 5y.
и |
|
|
|
|
|
||
|
y |
||||||
|
область |
|
|||||
|
|
Вариант 5 |
|
|
|
|
|
1. |
Найти |
определения функции z |
|
1 y x2 . |
|||
2. |
Найти частные производные функции z |
x |
2x2 y. |
||||
|
|||||||
3. |
Найти градиент функции z y2 в точке |
1; 1 . |
|||||
|
|
x3 |
|
|
|
|
|
4. |
|
Д |
|||||
Составить уравнения касательной плоскости к поверхности |
|||||||
z x3y xy2 |
в точкеАK 1; 2 . |
||||||
5. |
Найти частные производные второго порядка функции |
||||||
z (x2 y2)x.
1.Найти область определения функции zИarcsin y .
x2
2.Найти частные производные функции z (x2 2y)y 5x.
3.Найти градиент функции z arcctg(x2 y)в точке B 1; 1 .
4.Составить уравнения касательной плоскости к поверхности
z 2x2 y xy2 в точке C 1; 1 .
27

5. Найти частные производные второго порядка функции
zyln x ln y.
6.Исследовать на экстремум функцию z 3x 6y x2 xy y2.
|
|
|
|
|
Вариант 7 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1. |
Найти область определения функции z |
9 x2 |
y2 |
. |
||||||||||||||
Найти |
|
|
|
|
|
y |
||||||||||||
2. |
Найти частные производные функции z 2 x |
|
|
x ln y. |
||||||||||||||
|
|
|||||||||||||||||
С |
|
x |
|
|
|
|
|
2 |
||||||||||
3. |
|
|
град ент функции z |
|
в точке C 5; 1 . |
|||||||||||||
|
|
y2 |
||||||||||||||||
4. |
|
бА |
|
к поверхности |
||||||||||||||
|
Состав ть уравнения касательной плоскости |
|
||||||||||||||||
z 2x |
2 |
4xy |
2 |
в точке D 2; 1 . |
|
|
|
|
|
|
|
|
|
|
|
|||
5. |
|
Найти |
частные производные |
второго |
|
порядка функции |
||||||||||||
z ln(3x y). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
6. |
Исследовать на экстремум функцию z y2 x2 |
xy 2x 6y. |
||||||||||||||||
|
|
|
|
|
Дx |
|||||||||||||
|
|
|
|
|
Вариант 8 |
|
|
|
|
|
|
|
|
|||||
1. |
Найти область определения функции z |
|
|
x y |
|
. |
|
|||||||||||
x |
2 y2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2. |
Найти частные производные функции z |
2 |
y |
|
2xy2. |
|||||||||||||
|
|
|
||||||||||||||||
|
||||||||||||||||||
3.Найти градиент функции z ln(2x 3y) в точке D 1; 1 .
4.Составить уравнения касательной плоскости к поверхности
z x2 y 2x2 3xy 2 |
в точке N 1; |
1 . |
И |
||
|
|||||
5. |
Найти частные производные второго порядка функции |
||||
z |
y2 |
x3y. |
|
|
|
x |
|
|
|
||
|
|
|
|
|
|
6. Исследовать на экстремум функцию z 2xy 3x2 2y2 10.
28

|
|
|
Вариант 9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1. |
Найти область определения функции z |
|
|
2x y2 . |
|
|||||||||||||||
2. |
Найти частные производные функции z |
|
2x |
y |
2 |
|
x. |
|
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
С |
|
|
2x 3y |
|
|
|
|
|
y |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3. |
Найти градиент функции z |
в точке F 1; 1 . |
||||||||||||||||||
|
||||||||||||||||||||
|
|
|
|
|
x2 y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
4. |
остав ть уравнения касательной плоскости к поверхности |
|||||||||||||||||||
Найти |
Вариант 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
z x2 y 2y2 5x в точке 1; 2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5. |
|
частные |
производные |
второго |
|
порядка |
функции |
|||||||||||||
z ey |
cos x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. |
Исследовать на экстремум функцию z 4(x y) x2 |
y2 . |
||||||||||||||||||
|
область |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
x2 |
y2 |
|
|
|
||||||||||
1. |
Найти |
А |
5 . |
|
||||||||||||||||
определения функции z |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
x2 |
|
y |
|
|
||||||||
2. |
Найти частные производные функции z |
|
|
|
|
|
|
. |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
y |
|
x |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3. |
Найти градиент функции z x ey |
5xy 2y в точке A 1; 0 . |
||||||||||||||||||
4. |
Составить уравнения касательной плоскости к поверхности |
|||||||||||||||||||
z 3xy y3 8x в точке D(1; 2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
5. |
Найти |
частные |
производные |
второго порядка функции |
||||||||||||||||
|
|
|
|
|
|
|
И |
|||||||||||||
z ex |
cos y sin x ey. |
|
Д2 2 |
|||||||||||||||||
6. Исследовать на экстремум функцию z x |
xy |
y |
|
|
x y 1. |
|||||||||||||||
29
