
- •ВВЕДЕНИЕ
- •Раздел 1. МАТЕМАТИЧЕСКИЙ АНАЛИЗ
- •1. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- •1.1. Определение и основные понятия
- •1.3. Элементы скалярного поля
- •1.4. Локальный экстремум функции двух переменных
- •1.5. Метод наименьших квадратов
- •2. НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
- •2.1. Первообразная функция и неопределенный интеграл
- •2.2. Замена переменной в неопределенном интеграле
- •2.3. Интегрирование по частям
- •2.4. Интегрирование рациональных дробей
- •2.4.3. Интегрирование неправильных рациональных дробей
- •3. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
- •3.1. Определенный интеграл, его свойства
- •3.2. Формула Ньютона – Лейбница
- •3.3. Методы вычисления определенного интеграла
- •3.3.1 .Замена переменной в определенном интеграле
- •3.4.4. Длина дуги плоской кривой
- •3.5. Несобственные интегралы
- •4. КОМПЛЕКСНЫЕ ЧИСЛА
- •Комплексные числа и действия над ними
- •5.1. Основные понятия
- •5.2. Дифференциальные уравнения первого порядка
- •6. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
Раздел 1. МАТЕМАТИЧЕСКИЙ АНАЛИЗ
1. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Математический анализ представляет собой основу всей |
||||||||||
С |
|
|
|
|
|
|
|
|
||
высшей математики. Его содержание составляют дифференциальное |
||||||||||
и интегральное исчисления функции одной и нескольких переменных. |
||||||||||
|
1.1. Определение и основные понятия |
|
|
|||||||
ями |
явлений |
приходится |
встречаться |
с |
||||||
При |
зучен |
многих |
||||||||
функц |
двух |
олее независимых переменных. |
Например, |
при |
||||||
вычислен |
площади прямоугольника каждой паре его длины |
x |
и |
|||||||
|
бА |
, значит, S |
есть |
|||||||
ширины y соответствует определённое число S x y |
||||||||||
функц я двух переменных. Введём понятие функции нескольких |
||||||||||
переменных. |
|
|
|
|
|
|
|
|
||
Если каждой паре (x, y) |
значений двух независимых друг от |
|||||||||
друга переменных величин x и y из некоторой области их изменения |
||||||||||
D по какому-ли о |
правилу ставится |
в соответствие одно вполне |
||||||||
определённое значение величины z, то переменная z называется |
||||||||||
функцией двух переменных x и y, определённая в области D. |
|
|
||||||||
Символически |
функция |
Д |
так: |
|||||||
двух переменных обозначается |
||||||||||
z f (x, y), z F(x, y) и т.д. |
|
|
|
|
|
|
|
|||
Функция двух переменных может быть задана, например, с |
||||||||||
помощью таблицы или аналитически – с помощью формулы. |
|
|
||||||||
Пример 1. Вычислить частное значение функции |
|
|
||||||||
|
|
|
|
|
|
|
И |
|||
f (x,y) |
x2 y2 при x 5; |
y |
3. |
|
||||||
|
|
|
|
|
||||||
Решение. Подставляя |
значения аргументов x 5 и y 3 |
в |
||||||||
|
|
|
|
|
|
|
|
|||
функцию, получим f (5; 3) |
|
52 ( 3)2 |
4. |
|
|
|
|
|||
Совокупность пар (x, y) значений x и y, при которых определяется функция z f (x, y), называется областью определения этой функции.
Область определения функции двух переменных наглядно иллюстрируется геометрически. Если каждую пару значений переменных x и y изображать точкой M(x, y) в плоскости Oxy, то область определения функции изобразится в виде некоторой
4

совокупности точек на плоскости. В частности, областью определения может быть и вся координатная плоскость.
Определение функции двух переменных легко обобщить на
случай трёх или более переменных. |
|
|
|
|
|
|
|
||||||
Пример |
2. |
|
Найти |
|
область |
определения |
функции |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С |
|
|
|
|
|
|
|
|
|
|
|||
f (x,y) 4 x2 |
y2 . |
|
|
|
|
|
|
|
|
|
|
||
Решение. Для того чтобы функция существовала, нужно, чтобы |
|||||||||||||
под корнем стояло неотрицательное |
число, |
т. |
е. |
x |
и y |
должны |
|||||||
удовлетворять неравенству |
4 x2 y2 |
0, |
или |
x2 |
y2 |
22 |
. Делаем |
||||||
определения |
|
|
|
|
|
|
|
|
|||||
вывод, что все точки |
M(x, y), координаты которых удовлетворяют |
||||||||||||
указанному неравенству, лежат в круге с радиусом 2 с центром в |
|||||||||||||
начале коорд нат на границе этого круга. |
|
|
|
|
|
|
|||||||
|
бА |
|
|
|
|||||||||
Так же, как |
для функции двух переменных, можно говорить об |
||||||||||||
области |
|
я функции трёх, четырёх и более переменных. |
|||||||||||
Областью |
|
|
|
|
функции |
трёх |
переменных |
является |
|||||
некоторая совокупность точек пространства, однако область |
|||||||||||||
определен я |
функц |
четырёх и |
более |
переменных |
уже не |
||||||||
допускает простого геометрического истолкования.
Графиком функции двух переменных является поверхность,
проектирующаяся на |
|
плоскости |
Oxy |
в область |
определения этой |
|
функции. |
|
|
Д |
|||
|
|
|
||||
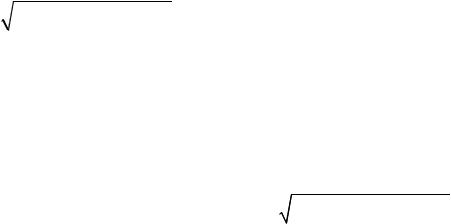
Пример 3. Построить график функции z x2 y2. |
||||||
Решение. |
В |
|
сечениях |
поверхности |
вертикальными |
|
координатными плоскостями получаются параболы z x2 и z y2 , а |
||||||
плоскостью, |
параллельной плоскости Oxy |
– окружность |
||||
x2 y2 C(рис.1.1). |
Следовательно, |
И |
||||
графиком |
функции является |
|||||
параболоид вращения. |
|
|
|
|
||
|
|
|
|
z |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
Р |
|
|
|
|
|
y |
О |
x |
|
|
|
|
|
|
|
|
Рис. 1.1
5
Функцию трёх или более переменных изобразить с помощью графика в пространстве невозможно.
В отличие от функции одной действительной переменной
функция z f (x, y) |
имеет три вида приращений. |
|
|
|
|
|
|||||||||||||||
|
Если |
y |
сохраняет |
постоянное |
значение, |
а |
x |
получает |
|||||||||||||
приращение |
|
x, |
|
|
то |
|
z |
|
|
получает |
|
приращение |
|||||||||
xz f (x x,y) f (x, y), |
называемое частным приращением z |
по |
|||||||||||||||||||
x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
Аналог чно, |
если |
|
x |
сохраняет постоянное значение, а |
||||||||||||||||
приращен |
, то z |
|
получает |
приращение |
|||||||||||||||||
получает |
пр ращен е |
y |
|
||||||||||||||||||
Сz f (x,y) f (x, y y), |
называемое частным приращением z |
по |
|||||||||||||||||||
|
y |
бА |
|
|
|
|
|||||||||||||||
y. |
|
|
|
|
|||||||||||||||||
|
Наконец, соо щ в аргументу x |
приращение |
x, а аргументу y |
||||||||||||||||||
|
|
е y, получим |
для |
функции |
|
z ещё |
одно |
приращение |
|||||||||||||
z f (x x, y y) f (x, y), |
|
которое |
|
называется |
полным |
||||||||||||||||
приращен ем функц |
z. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Окрестностью радиуса r точки M0(x0,y0) называется |
||||||||||||||||||||
совокупность |
всех |
точек |
(x, y), |
удовлетворяющих |
неравенству |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
(x x )2 (y y )2 |
r. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть |
дана |
функция |
z f (x, y), |
определённая |
в |
некоторой |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|
||||||||
области G плоскости Oxy. Рассмотрим некоторую точку |
M0(x0,y0), |
||||||||||||||||||||
лежащую в области G или на её границе. |
|
|
|
|
|
|
|
|
|||||||||||||
|
Число A называется пределом функции |
|
z f (x, y) |
при |
|||||||||||||||||
стремлении точки M(x, y) к точке M0(x0,y0), если для каждого числа |
|||||||||||||||||||||
0 найдётся |
такое |
|
число |
r 0 , |
что |
|
для всех точек M(x, y), |
||||||||||||||
удовлетворяющих неравенству |
(x x )2 (y y )2 |
r, |
имеет место |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
неравенство |
|
|
f (x,y) A |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Если число A является пределом |
функции |
z f (x, y) |
при |
|||||||||||||||||
стремлении |
точки |
M(x, y) |
к |
точке |
M |
(x ,y ), |
то |
записывают |
|||||||||||||
lim f (x, y) A. |
|
|
|
|
|
|
|
|
|
|
0 И0 0 |
||||||||||
x x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть точка M0(x0,y0) принадлежит области определения |
||||||||||||||||||||
функции z f (x, y). Функция |
|
z f (x, y) |
называется непрерывной в |
||||||||||||||||||
6

точке M0(x0,y0), если имеет место равенство |
lim f (x,y) f (x0,y0), |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
x x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y y0 |
|
|
|
|
|
|
причём точка M(x, y) стремится к точке M0(x0,y0) произвольным |
||||||||||||||||
образом, оставаясь в области определения функции. |
|
|
|
|
|
|
||||||||||
Если в некоторой точке N0(x0,y0) не |
выполняются |
условия |
||||||||||||||
непрерывности, то точка N0(x0,y0) называется точкой разрыва |
||||||||||||||||
функции z f (x, y). |
|
|
sin(xy) |
|
|
|
|
|
|
|
|
|||||
Пр мер 4. Найти предел lim |
. |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
вшись |
|
y |
|
|
|
|
|
|
|
|
|
|||||
СРешен е. Убед |
|
x 3 |
|
|
|
|
|
|
|
|
|
|
||||
|
y 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
, что функция не определена в предельной |
||||||||||||||||
точкеN0(3;0), делаем прео разования: |
|
|
|
|
|
|
|
|||||||||
|
бА |
|
sin x |
|
|
|
||||||||||
lim |
sin(xy) |
lim x lim |
sin(xy) |
3 1 3, так как lim |
1. |
|
||||||||||
x 3 |
y |
x 3 |
x 3 |
xy |
|
|
|
|
|
|
x 0 |
x |
|
|
||
y 0 |
|
y 0 |
y 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Пр мер 5. Указать точки разрыва функции f (x, y) |
x y |
. |
||||||||||||||
|
|
|
|
|
|
|
|
x y |
|
|
|
x2 3y2 |
|
|||
Решение. |
Функция |
f (x, y) |
x |
2 3y2 |
определена |
на всей |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
плоскости Oxy, но не существует в точке M0(0;0), поэтому в этой точке функция терпит разрыв. Во всех других точках плоскости она
непрерывна. |
|
|
|
|
|
|
|
|
|
|
|
Пример 6. |
Найти |
и |
исследовать |
точки |
разрыва |
||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
функции |
f (x,y,z) x2 y22 z2 . |
|
|
||||||||
|
|
|
|
|
|
|
|
|
И |
||
Решение. Для этой функции трёх переменных точки разрыва |
|||||||||||
лежат на конусе |
x |
2 |
y |
22 |
z |
2 |
Д |
||||
|
|
|
0, так как |
знаменатель дроби не |
|||||||
должен равняться нулю. |
|
|
|
|
|
|
|
||||
|
Задачи для самостоятельного решения |
|
|||||||||
1. Для |
функции |
|
f (x, y) |
2x y |
вычислить значения: |
f (1;2), |
|||||
|
|
||||||||||
|
|
|
|
|
|
|
|
x 2y |
|
|
|
f(3;1), f (a;2a), f (2b; b).
2.Найти область определения функций:
а) z x2 xy2 y3 1; б) |
f (x,y) 2 x2 2y2 ; |
7
в) z |
|
|
|
2 |
|
|
|
; |
|
|
|
г) z |
|
|
|
|
1 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
2x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
x2 y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
д) z |
ln(x2 y) |
; |
|
|
е) |
z arccos(x2 |
y2). |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
y x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3. Найти пределы функций двух переменных: |
|
|
1 |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
a |
|
a2 xy |
|
|
|
|
|
|
xy2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
а) lim |
|
|
|
; б) lim |
|
|
|
; в) lim (1 2xy |
xy |
); |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
y 0 |
|
|
|
|
|
xy |
|
|
|
y 1 |
|
|
sin(xy) |
|
|
|
y 0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|||
точки |
xy2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
г) lim |
|
|
arctg2x3 y |
; д) lim |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Сx 2 ln(1 xy) |
|
|
x 0 |
|
exy 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
y 0 |
|
|
|
|
|
|
|
|
|
|
|
y 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Указать |
|
|
|
|
|
ли линии разрыва функций: |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
бА |
y2 |
|
|
|
||||||||||||||||||||||||||||||||
а) z |
|
|
|
|
|
|
2y |
|
|
|
; ) |
z |
|
|
x |
y |
; в) z |
|
|
|
. |
|
|||||||||||||||||
|
(x 1)2 (y 2)2 |
|
|
|
|
|
|
|
2x y |
|
|
|
|
|
|
x2 |
4y2 4 |
|
|||||||||||||||||||||
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
Ответы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1.0; 5; |
0; |
4 |
. |
|
2. |
а) вся числовая плоскость; |
б) |
|
точки, лежащие |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x2 2y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
внутри эллипса |
2 и на этом эллипсе; |
|
в) |
вся плоскость |
|||||||||||||||||||||||||||||||||||
Oxy, кроме точек, лежащих на прямых y x; |
|
г) |
x 0; y 0 ; |
||||||||||||||||||||||||||||||||||||
д) y x ; |
y 0 |
|
, x 0 ; е) круг x2 |
y2 |
|
1. 3. а) |
1 |
; б) 1; в) e2 ; г) 8; |
|||||||||||||||||||||||||||||||
|
|
2a |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д) 2. 4. а) одна точка разрыва (1; 2); б) линия разрыва – прямая |
|||||||||||||||||||||||||||||||||||||||
y 2x; линия разрыва – гипербола x2 |
4y2 |
4. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||||||||||
1.2. Частные производныеДи дифференциал функции |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
нескольких переменных |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Частной производной по х функции |
|
z f (x, y) называется |
|||||||||||||||||||||||||||||||||||||
предел частного приращения xz |
|
к приращению x при стремлении |
|||||||||||||||||||||||||||||||||||||
x к нулю произвольным образом. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Частная |
производная |
функции z f (x, y) |
по |
аргументу |
х |
||||||||||||||||||||||||||||||||||
является обыкновенной производной функции одной переменной |
х |
||||||||||||||||||||||||||||||||||||||
при фиксированном значении переменной у и обозначается как |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
, zx , |
fx (x, y). |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
8

Таким образом, по определению,
|
|
|
|
|
|
|
z |
lim |
f (x x, y) f (x, y) |
. |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
x |
|
x 0 |
|
x |
|
|
|
|
|||||||
Аналогично определяется и обозначается частная производная по |
||||||||||||||||||||||
у от функции z f (x, y): |
z |
, или zy , |
или fy (x, y). |
|
|
|
|
|||||||||||||||
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
||
Знач т, |
z |
lim |
f (x, y y) f (x, y) |
. |
|
|
|
|
||||||||||||||
y |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
x 0 |
|
|
|
|
y |
|
|
|
|
|
у, а |
y z |
|
||||
Замет в, что xz |
|
вычисляется при постоянном |
при |
|||||||||||||||||||
неизменном |
|
|
х, |
делаем |
вывод, |
что |
правила вычисления |
частных |
||||||||||||||
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
производных совпадают с правилами, указанными для функций одной |
||||||||||||||||||||||
переменной; только тре уется каждый раз помнить, по какой |
||||||||||||||||||||||
переменной |
|
щется про зводная. |
|
|
|
|
|
|
|
|
||||||||||||
Аналог чно |
|
|
|
функцию |
|
u f (x, y,z,...,t) |
можно |
|||||||||||||||
|
|
ровать по каждому из её аргументов, считая при этом все |
||||||||||||||||||||
дифференц |
|
|
|
|
|
|
|
|
|
|||||||||||||
остальные аргументы постоянными. |
|
|
|
|
|
|
|
|
||||||||||||||
Если |
функц я |
|
z f (x, y) |
имеет непрерывные |
частные |
|||||||||||||||||
производные в данной точке, а её полное приращение можно |
||||||||||||||||||||||
представить в виде суммы |
|
|
|
|
|
|
|
|
|
|||||||||||||
z |
z |
x z y 1 x 2 y (где величины |
1 и |
2 |
||||||||||||||||||
|
||||||||||||||||||||||
|
x |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
стремятся к нулю, когда x и |
y |
стремятся к нулю), то она |
||||||||||||||||||||
|
бА |
|
|
|
|
|||||||||||||||||
называется |
дифференцируемой в этой точке, а линейная часть |
|||||||||||||||||||||
приращения называется полным дифференциалом и обозначается |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
dz fx (x,y)dx fy (x, y)dy. |
|
|
|
|
||||||||
В последнем |
равенстве |
дифференциалы |
независимых |
|||||||||||||||||||
переменных |
|
|
х |
и у |
|
равны |
Д |
т.е. |
||||||||||||||
|
|
|
их |
приращениям |
x |
и |
y, |
|||||||||||||||
dx x; dy y.
Таким образом, полный дифференциал функции равен сумме
произведений |
частных |
производных |
на |
дифференциалы |
соответствующих независимых переменных. |
|
|||
При достаточно малых |
|
И |
||
x и y полное приращение функции |
||||
z f (x, y) приближённо равно её полному дифференциалу z dz. Отсюда получим формулу для приближённого вычисления величин
f (x x, y y) f (x, y) f (x, y) x f (x, y) y,
x y
9
верную с точностью до бесконечно малых высшего порядка
относительно |
x и y. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Если |
поверхность задана |
уравнением |
F(x, y,z) 0 |
и точка |
||||||||||||||||||||||||||||||||||
M0(x0,y0,z0) лежит на ней, то касательная плоскость к поверхности |
||||||||||||||||||||||||||||||||||||||
в точке M0 |
определяется уравнением |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
(x x0)Fx (M0) (y y0)Fy (M0) (z z0)Fz (M0) 0. |
||||||||||||||||||||||||||||||||||||||
Нормаль |
|
к |
|
поверхности |
|
|
|
в |
точке |
|
|
|
M0(x0, y0,z0)(прямая, |
|||||||||||||||||||||||||
проходящая через эту точку перпендикулярно к касательной |
||||||||||||||||||||||||||||||||||||||
дифференц |
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
u |
|
|
u |
|
||||||||||||||||
плоскости) определяется уравнениями |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
С |
|
(x x ) |
|
|
(y y ) |
|
|
(z z ) |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
. |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
Fx(M0) Fy(M0) Fz(M0) |
|
|
|
|
|
|||||||||||||||||||||||||||
Функц ю |
|
|
мног х |
|
переменных |
|
|
|
|
u f (x, y,z,...,t) |
можно |
|||||||||||||||||||||||||||
|
бА |
|
|
|
||||||||||||||||||||||||||||||||||
|
ровать по каждому из её аргументов. Полученные |
|||||||||||||||||||||||||||||||||||||
частные про зводные первого |
порядка |
x |
, |
|
|
|
y |
, …, |
|
t |
обычно |
|||||||||||||||||||||||||||
зависят от тех же аргументов и каждую из них можно также |
||||||||||||||||||||||||||||||||||||||
дифференцировать по каждому аргументу. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Пусть |
в |
уравнении |
|
z F(u,v) переменные |
u и |
v |
являются |
|||||||||||||||||||||||||||||||
функциями независимых переменных х и y: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
u (x, y),v (x, y). |
|
|
|
|
|
|||||||||||||||||||||||||
В таком случае z |
|
|
|
|
|
|
|
|
|
|
Д |
|||||||||||||||||||||||||||
называется сложной функцией от аргументов х |
||||||||||||||||||||||||||||||||||||||
и y. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если |
|
|
функции |
|
|
|
|
|
двух |
|
|
|
|
|
переменных |
|
z F(u,v); |
|||||||||||||||||||||
u (x, y),v (x, y) |
имеют непрерывные частные производные по |
|||||||||||||||||||||||||||||||||||||
всем своим аргументам, то производные сложной функции равны |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
z |
|
|
|
F |
|
|
|
u |
|
|
|
F |
|
|
|
v |
; |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
u |
|
x |
|
|
v |
|
|
|
|
x |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
z |
|
F |
|
u |
|
F |
|
v |
. |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
y |
|
|
|
u |
|
y |
|
|
v |
|
|
|
|
y |
|
|
|
|
|
||||||||||
Рассмотрим функцию двух переменныхИz f (x, y). Частные |
||||||||||||||||||||||||||||||||||||||
производные |
|
z |
|
и |
|
z |
|
в |
|
общем |
случае |
|
|
являются |
|
функциями |
||||||||||||||||||||||
|
x |
|
|
y |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
переменных х и |
|
y. Поэтому от них можно снова находить частные |
||||||||||||||||||||||||||||||||||||
производные. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10
Частные производные от частных производных первого порядка называются частными производными второго порядка. Они обозначаются так:
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
у |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
С |
|
|
|
|
х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
|
|
х2 |
|
|
zхх; |
|
|
у |
|
|
|
|
|
|
|
уу; |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
у2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
у |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
у |
|
|
|
x y |
|
z |
ху ; |
|
|
х |
|
|
|
|
y x z |
ух . |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Про зводные второго порядка можно снова дифференцировать |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
по каждому аргументу. Получим частные производные третьего |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
порядка. Их будет уже восемь: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
бА |
|
|
|
|
|
3z |
|
|
3z |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3z |
, |
|
3z |
|
|
|
, |
|
|
|
3z |
|
|
, |
|
|
|
3z |
|
, |
|
3z |
|
|
, |
|
|
3z |
|
|
|
, |
|
|
, |
|
. |
|
|||||||||||||||||||||||||
|
x |
3 |
|
|
|
|
|
2 |
y |
|
|
|
x y x |
|
|
x y |
2 |
|
y x |
2 |
|
|
|
|
y x y |
|
|
|
2 |
y x |
|
|
y |
3 |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
Теорема. |
Если функция z f (x, y) имеет непрерывные частные |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
производные в точке M(x, y) |
|
|
и в некоторой её окрестности, |
то в этой |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
точке справедливо равенство |
2z |
|
2z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x y |
|
y x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|
|
|
||||||||||||||||||||||||||||
Пример 1. Вычислить значения частных производных первого |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
порядка |
функции |
|
|
|
|
z x2 5xy2 y3 |
при |
|
|
указанных |
значениях |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
аргументов: x 1;y 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Решение. |
Считая |
|
z |
|
|
функцией |
только одного |
|
аргумента |
х, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
находим производную zx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|||||||||||||||||||||||||||||||||||||||||||
2x 5y2, аналогично, |
|
считая z |
функцией |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
только |
одного |
|
|
|
|
аргумента |
|
|
y, |
|
находим |
|
|
другую |
|
|
производную |
|||||||||||||||||||||||||||||||||||||||||||||||
zy 10xy 3y2. |
|
|
|
Затем вычисляем их частные значения в указанной |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
( 1;1) 3; |
|
|
( 1;1) 13. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
точке: zx |
zy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
Пример 2. Найти частные производные первого порядка от |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
функции u |
x |
|
y |
|
z |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
y |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Решение. Считая u функцией только одного аргумента х, затем только y и только z, получим три частные производные:
11

u |
|
1 |
|
z |
; |
u |
|
x |
|
1 |
; |
u |
|
y |
|
1 |
. |
x y x2 |
|
y |
|
y2 |
|
z z |
|
z2 |
|
x |
|||||||
Пример 3. Найти частные производные первого порядка от функции z x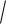 ey .
ey .
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Решение. Заменяя корень степенью с дробным показателем и |
||||||||||||||||||||||||||||||||||||||||||
затем дифференцируя как сложную функцию по каждой из двух |
||||||||||||||||||||||||||||||||||||||||||
переменных, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
z |
e |
y |
; |
|
|
y |
e |
y |
|
1 |
|
y |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
x |
|
x |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
zx |
|
; zy xe |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4y |
|
|
|
||||||||||||||||
поверхности |
|
|
|
|
|
|
|
|
3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Пр мер 4. Найти уравнение касательной плоскости и нормали к |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
, заданной уравнением z |
|
|
3x2 |
4y2 |
|
в точке M(2;1). |
|
|
|
||||||||||||||||||||||||||||||
Решен . |
Прео разуя |
|
|
уравнение |
|
|
|
|
|
поверхности |
к |
|||||||||||||||||||||||||||||||
виду |
3x2 4y2 |
z 0 и о означив его левую часть через F(x, y,z), |
||||||||||||||||||||||||||||||||||||||||
найдём |
частные |
про зводные |
|
Fx |
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
Fy |
|
|
|
|
|
|
|
; |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3x2 4y2 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x2 4y2 |
|
|
|
|
|
|
|
|
|
||||||||||||||
Fz 1. Затем вычислим их значения в данной |
точке |
Fx (M) |
3 |
; |
||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||
Fy (M) 1 и значение z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||
z(M) 4. Получим уравнение касательной |
||||||||||||||||||||||||||||||||||||||||||
плоскости |
3 |
(x 2) 1 (y 1) (z 4) 0 или |
3 |
x y z 0. |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
Дx |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
бА(x 2) (y 1) |
|
|
(z 4) |
|
|
|
||||||||||||||||||||||||||||||||||
Уравнения нормали будут иметь вид |
|
|
3 |
|
|
|
|
1 |
|
|
|
1 |
. |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||||||||||||||||||
Пример 5. Проверить, что |
функция |
z xln |
y |
удовлетворяет |
||||||||||||||||||||||||||||||||||||||
уравнению x |
z |
y |
z |
z. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
x |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение. Преобразуем функцию, используя свойства логарифмов z x(ln x ln y). Найдём частные производные по х и по y:
z |
ln y ln x 1 ln |
y |
1; |
z |
|
x |
. |
x |
|
x |
y y |
||||
12
Подставляя z, |
z |
|
и |
|
z |
в данное уравнение, получим тождество |
||||||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
x |
|
y |
|
|
|
y |
|
||||||
x(ln |
y |
1) y |
x |
xln |
y |
; |
0=0. |
Это значит, что функция z xln |
|
|||||||||
x |
|
|
x |
|||||||||||||||
|
|
y |
|
x |
|
|
z |
|
z |
|
||||||||
удовлетворяет уравнению x |
y |
z. |
||||||||||||||||
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
y |
||||
Пр мер 6. Найти полный дифференциал функции z 3x2 y5. Решен е. Наход м частные производные первого порядка
дифференц |
5 |
|
|
2 |
4 |
|
||
данной функц |
: |
|
|
|
|
|
|
|
С |
z 6xy5 ; |
z |
15x2 y4 . |
|
||||
|
|
x |
|
y |
|
|
|
|
Затем, умножая |
частные |
производные на |
соответствующие |
|||||
бАz 3 z z 2 z |
2 |
|||||||
алы незав симых переменных и складывая полученные |
||||||||
выражен я, найдём скомый полный дифференциал функции: |
||||||||
|
|
dz 6xy dx 15x |
|
y dy. |
|
|||
Пр мер 7. Найти частные производные второго порядка |
||||||||
функции z x3 |
5x2 y3 |
y2 . |
|
|
|
|
|
|
Решение. Сначала находим частные производные первого порядка, затем искомые частные производные второго порядка:
|
|
|
|
z |
3x2 10xy3; |
z |
15x2 y2 2y; |
|||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
x |
|
|
Д |
|||||||||
|
|
|
|
|
|
|
y |
|
|
|
|
|
||||
2 |
6x 10y ; |
2 |
|
2 |
|
|
|
|
2 |
|
||||||
|
х2 |
x y |
y x 30xy ; |
|
у2 |
30x y 2. |
||||||||||
Пример 8. |
Проверить, |
что |
для |
функции z cos(ax by) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
И |
|||||
выполняется равенство zxy zyx . |
|
|
|
|
|
|
|
|
||||||||
Решение. Найдём частные производные первого порядка: |
||||||||||||||||
|
|
|
zx |
asin(ax by); zy bsin(ax by). |
||||||||||||
Затем, дифференцируя zx по y, получим |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
abcos(ax by). |
|||||
|
|
(zx )y zxy ( asin(ax by))y |
||||||||||||||
Аналогично |
|
|
|
|
|
|
|
|
abcos(ax by). |
|||||||
(zy )x zyx (bsin(ax by))x |
||||||||||||||||
Сопоставляя |
полученные |
результаты, |
|
заключаем, что для |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
данной функции выполняется равенство zxy |
zyx . |
|||||||||||||||
13
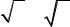
Пример 9. Проверить, |
что в точке M( |
2 |
; |
4 |
) |
функция |
|
|
|||||
z x3 3x2 4xy y2является |
3 |
3 |
|
|
||
стационарной (производная |
в любом |
|||||
направлении равна нулю).
Решение. Найдём частные производные первого порядка: |
||||||||||||||||||||||||||||||||||||||||||||
С |
zx |
|
3x2 6x 4y; zy 4x 2y. |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
Подставляя в н х координаты данной точки, вычисляем |
||||||||||||||||||||||||||||||||||||||||||||
|
|
zx(M) 3 |
4 |
|
6 |
2 |
4 |
4 |
|
|
0; zy (M) 4 |
2 |
2 |
4 |
0. |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
Найти |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
3 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
9 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Пр мер |
10. Дана |
сложная |
функция |
z ln(2u 3v), где |
||||||||||||||||||||||||||||||||||||||||
u x2y;v xy y3. |
|
|
|
|
|
|
частные производные |
z |
|
|
и |
z |
. |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
y |
|
|
|
|
|
|
бА |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
Решен е. |
Найдём частные производные первого порядка : |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
z |
|
|
|
2 |
|
; |
z |
|
|
3 |
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
u |
|
|
|
|
|
|
2u 3v |
|
v |
|
|
|
|
2u 3v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
u |
|
2xy; |
v |
y; |
|
u |
x |
2 |
; |
v |
x |
3y |
2 |
. |
|
|
||||||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
y |
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Подставляя найденные выражения в формулу для нахождения |
||||||||||||||||||||||||||||||||||||||||||||
частных производных сложной функции, получим |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
z |
|
|
|
2 |
|
|
2xy |
|
|
|
3 |
|
|
|
y; |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
x |
|
|
2u 3v |
Д |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2u |
3v |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
z |
|
|
2 |
|
|
x2 |
3 |
|
(x 3y2). |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
y |
|
|
2u 3v |
|
|
|
|
2u 3v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
1. z x2 |
2xy 2y2 |
. Найти (zx |
|
|
|
|
|
|
|
И |
||||||||||||||||||||||||||||||||||
zy ) в точке ( 1;1). |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
2. Найти сумму частных производных первого порядка функции |
||||||||||||||||||||||||||||||||||||||||||||
z arctg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z ln( |
|
|
|
|
|
|
|
) |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
3. Проверить, что функция |
|
|
|
|
|
|
|
удовлетворяет |
||||||||||||||||||||||||||||||||||||
|
x |
|
|
y |
|
|
||||||||||||||||||||||||||||||||||||||
уравнению x |
z |
y |
z |
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
y |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4. Найти сумму частных производных первого порядка функции |
||||||||||||||||||||||||||||||||||||||||||||
u y2ez ln(x2 |
2y) в данной точке (1; 1;0). |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
14
5. Составить уравнение касательной плоскости и нормали к
поверхности x2 2y2 |
3z2 |
6 |
в точке (1; 1;1). |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
6. оставить уравнение касательной плоскости и нормали к |
|||||||||||||||||||||||||||||||||||||||||
поверхности z 2x2 |
4y2 в точке (2;1;12). |
|
|
|
2 |
|
|
|
|
|
x |
|
|
|
|
||||||||||||||||||||||||||||
С |
|
|
|
|
значение |
полного |
|
|
|
|
|
|
|
|
|
функции |
|||||||||||||||||||||||||||
7. |
|
Вычислить |
|
|
дифференциала |
||||||||||||||||||||||||||||||||||||||
|
z arcctg |
x |
|
при |
x 1;y 3;dx 0,01;dy 0,05. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8. |
|
|
Для |
|
|
функц |
z x3 xy2 x y y4 |
|
найти |
значение |
|||||||||||||||||||||||||||||||||
|
и x2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
выражен я (zxx |
|
zxy |
|
zyy ) в точке M( 1;1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
9. |
|
Провер ть, |
|
|
что |
функция |
z 2cos |
|
(y |
2 |
) |
удовлетворяет |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2z |
|
|
2z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
бА |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
уравнен ю |
2 |
x2 |
|
|
|
|
|
|
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
10. Провер ть, что для функции z |
y2 |
|
|
выполняется равенство |
|||||||||||||||||||||||||||||||||||||
|
2z |
|
2z |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
х у |
|
y x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
11. |
|
|
Проверить, |
|
что |
функция |
z ln(x2 |
y2 ) |
удовлетворяет |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2z |
|
|
|
|
2z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
уравнению |
|
|
|
|
|
|
|
|
|
|
|
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
x |
2 |
|
y |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
12. |
|
|
Проверить, |
что |
функция |
u arctg(2x t) |
удовлетворяет |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2u |
|
|
|
|
|
2u |
|
|
|
|
|
|
|
И |
||||||||||||||||||||
уравнению |
|
|
|
|
|
2 |
|
|
|
|
|
0. |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x t |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
13. |
Подсчитать |
приближённоДизменение функции z arctg |
y |
, |
|||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||
когда х изменяется от 2 до 2,1, а y – от 3 до 2,5. |
|
|
|
|
|
|
|
x |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
14. |
|
Найти частные производные |
z |
|
|
и |
|
|
z |
|
сложной функции |
||||||||||||||||||||||||||||||||
|
x |
|
|
y |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
z arctg |
, где u x sin y;v x cos y. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
z |
|
|
|
|
|
|
||||||
15. |
|
Найти |
|
частные |
производные |
|
и |
|
, |
если |
z u v2 ; |
||||||||||||||||||||||||||||||||
|
|
|
x |
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
||||||
u x2 |
sin y; |
v ln(x y). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
15
