4. КОМПЛЕКСНЫЕ ЧИСЛА

Комплексным

числом

z

называется

выражение следующего

вида:

z x i y,

y действ тельные

где x

числа; i

так называемая мнимая

единица, определяемая равенством

действительная

Сx Rez

i2

1, i 1;

мнимая

часть;

y Im z

часть

комплексного ч сла.

z x i y

алгебраической формой записи

Назовём выражен

бА

комплексного ч сла.

Комплексное ч сло z

называется сопряженным комплексному

числу

z , если Rez Rez, Imz Imz.

Другими словами,

если

z x i y, то z x i y.

Два комплексных числа z1 x1 i y1

и z2 x2

i y2 равны, если

их действительные и мнимые части соответственно равны:

z1 z2, если x1 x2 ;

y1 y2 .

Всякое комплексное

Д

число

z

x i y можно изобразить на

плоскости Oxy в виде точки M(x, y)

с координатами x и y. Обратно

каждой точке плоскости M(x, y) соответствует комплексное число

z x i y. Плоскость, точки

которой

изображают комплексные

числа,

называется

плоскостью

комплексной переменной

z (на

плоскости ставят символ z

в кружок).

И

мнимой

оси,

а

именно

начало координат, изображает

действительное число нуль.

Соединив точку M(x, y) с началом координат, получим вектор

. В

некоторых

случаях удобно считать геометрическим

OM

изображения комплексного числа

z x i y вектор

.

OM

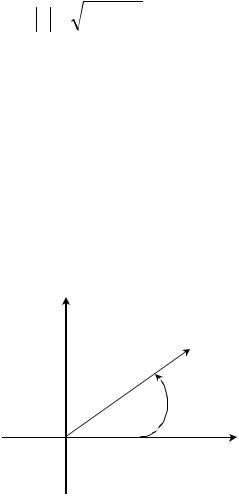
Рассмотрим

комплексное

число

z x i y,

которому

на

плоскости Oxy соответствует

точка M(x, y). Ее координатами в

полярной системе координат будет пара чисел

, .

Тогда по формулам перехода от декартовой системы координат к

полярной имеем

(рис.

4.1) x cos ;

y sin .

Подставим

эти

выражения

в

алгебраическую

форму комплексного

числа

z x i y cos i sin (cos i sin ).

Полученная

форма

комплексного

числа

называется

тригонометр ческой.

С

OM

называется модулем комплексного

Полярный рад ус

обозначается

z

.

Модуль

комплексного

числа

определяется

однозначно

по

2

2

числаформуле z x y .

Полярный угол

называется аргументом комплексного числа

и обозначается Arg z. Тогда

z cos i sin

z

cos Arg z i sin Arg z .

Аргумент комплексного числа определяется не однозначно, с

точностью до слагаемого 2 k,

где k

любое целое число. Главным

значением аргумента называется значение, заключенное в интервале

, . ОбозначаетсябАоно arg z. Таким образом, arg z .

Очевидно, Arg z arg z 2k .

y

Аргумент

комплексного

числа

считается

поло-

M x,y

Д

жительным, если он отсчи-

тывается

от

положительного

направления оси Ox, и

отрицательным

при проти-

x

воположномИнаправлении

отсчёта.

Сопряжённые

ком-

0

плексные числа имеют равные

модули, а их аргументы

отличаются знаком, но равны

Так как

tg arg z

y

, то главное значение аргумента

x

определяется однозначно следующим образом:

argz arctg

x

, если точка M(x, y)лежит в первой или четвёртой

y

С

четверти;

arg z arctg

x

, если точка M(x, y)лежит во второй четверти;

y

вид

argz arctg

x

, если точка M(x, y)лежит в третьей четверти.

y

z

z

бА

cos arg z 2k i sin arg z 2k .

Пусть

z x i y

z

cos Arg z i sin Arg z .

Используя

формулу

Эйлера cos i sin ei , получаем так

называемую

показательную форму записи комплексного числа:

z

z

ei Arg z .

учетом того, что i2 1; i3 i; i4 1.

Суммой

Д

iy2

двух комплексных чисел

z x1 iy1

и

z x2

называется комплексное число, определяемое равенством

x1 i y1 x2 i y2 x1 x2 i y1 y2 ;

множитель i, и члены, не содержащие множитель i:

Произведением

двух

комплексныхИчисел называется

Операции

сложения

и вычитания

сводятся к сложению и

вычитанию векторов, изображающих эти числа. Отсюда расстояние

между точками

z1,

z2

z1 z2

.

Деление комплексных чисел выполняется по правилу

С

z1

z1

.

z2

z2

z2 z2

Если комплексные числа заданы в тригонометрической форме

z1 r1 cos 1 isin 1 ;

z2 r2 cos 2

isin 2 ,

ми

то действ я над н

выполняют следующим образом:

z1z2 r1r2 cos 1

2 isin 1

2 ;

z1

r1 cos

2

isin

2

.

z2

r2

1

1

бА

Для возведен я комплексных чисел в

целую степень применяют

формулу Муавра

zn

rn cosn isinn .

Формула справедлива для целых положительных и

отрицательных

n.

Правило извлечения корня n-й степени из комплексного числа

n

2 k

2 k

z

n

z

cos

isin

k

n

n

,

то

Д

где k 0,1,2,...n 1.

Следовательно, корень n-й степени из комплексного числа

имеет n различных значений.

Уравнения вида xn A называются двучленными. Найдём корни

этого уравнения. Если

И

A есть действительное положительное число,

x n

A

(cos

2 k

isin

2 k

), где k 0,1,2,...n 1.

n

n

Выражение в скобках даёт все значения корня n-й степени из 1.

Если A – действительное отрицательное число, то

x n

(cos

2 k

isin

2 k

).

A

n

n

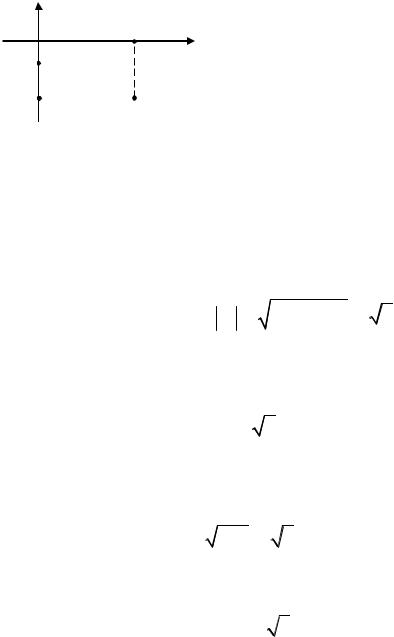
y

Пример

1.

Изобразить

0

z3

x

комплексные

числа

z1 5 5i;

-2 z2

5

z2 2i;

z3 5

точками на плоскости

Oxy.

-5

z1

Решение. Данным комплексным

числам будут соответствовать точки с

Р с. 4.2

координатами

M1(5, 5),

M2(0, 2).

число

M3(5,0) на плоскости Oxy (рис. 4.2).

Пр мер 2.

Нап сать в тригонометрической форме комплексное

Сz 1 i.

Решен е.

Найдём модуль и аргумент комплексного числа по

бА

приведённым выше формулам

z

( 1)2

12

2; tg 1; значит,

arg z arctg 1

3

.

4

4

Подстав м в формулу тригонометрической формы записи

комплексного числа и получим z

2(cos

3

isin

3

).

4

4

Пример 3. Представить в показательной форме комплексное

число z 1 i.

Решение. Найдём модуль и аргумент комплексного числа

z

Д

1 1 2;

tg 1;

arg z

3

, тогда показательная форма будет

4

4

3 i

1 i

2 e

.

4

Пример 4. Вычислить e

i

.

Решение. По формуле Эйлера можно представить

e i cos i sin 1.

Пример 5. Вычислить (2 i) (2 3i).

Решение. Выполним умножение комплексныхИчисел в

алгебраической форме

(2 i) (2 3i) 4 6i 2i 7i2 7 4i.

Пример 6. Вычислить

(2 i)

.

(2 3i)

2 i

(2 i)(2 3i)

4 2i 3i 3i2

4 5i

3( 1)

2 3i

(2 3i)(2 3i)

4 9i2

4 9(

1)

С

5

1 5i

1

i

.

13

13

16

i 5 .

Пр мер 7. Выч слить

3

Решен е. Найдём модуль и аргумент комплексного числа

и

1

z

3 i

3 1 2;

arg(

3 i) arctg(-

)

.

3

6

Преобразуем комплексное число к тригонометрическому виду

бА

3 i 2

cos

6

2k

i sin

6

2k

.

Затем для возведения в степень применим формулу Муавра

3 i

5

5

5

25 cos

6

10k

i sin

6

10k

3

1

32

i

16 3 16i.

2

2

Пример 8. Найти все значения корня 3 8.

Решение. Найдём

модуль

и

аргумент

комплексного

числа

z

8

8;

arg 8 .

Далее

запишем

комплексное

число в

тригонометрической форме

И

8 8 cos 2k

i sin

2k

.

Применим формулу извлеченияДкорня из комплексного числа

3

8

2(cos

2 k

isin

2 k

),

где k 0;1;2.

3

3