
- •ВВЕДЕНИЕ
- •Раздел 1. МАТЕМАТИЧЕСКИЙ АНАЛИЗ
- •1. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- •1.1. Определение и основные понятия
- •1.3. Элементы скалярного поля
- •1.4. Локальный экстремум функции двух переменных
- •1.5. Метод наименьших квадратов
- •2. НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
- •2.1. Первообразная функция и неопределенный интеграл
- •2.2. Замена переменной в неопределенном интеграле
- •2.3. Интегрирование по частям
- •2.4. Интегрирование рациональных дробей
- •2.4.3. Интегрирование неправильных рациональных дробей
- •3. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
- •3.1. Определенный интеграл, его свойства
- •3.2. Формула Ньютона – Лейбница
- •3.3. Методы вычисления определенного интеграла
- •3.3.1 .Замена переменной в определенном интеграле
- •3.4.4. Длина дуги плоской кривой
- •3.5. Несобственные интегралы
- •4. КОМПЛЕКСНЫЕ ЧИСЛА
- •Комплексные числа и действия над ними
- •5.1. Основные понятия
- •5.2. Дифференциальные уравнения первого порядка
- •6. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
Раздел 2. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Дифференциальные уравнения занимают особое место в |
||||
математике и имеют многочисленные приложения в большом спектре |
||||
С |
|
|
|
|
наук. Исследования многих процессов приводят к построению |
||||
математических |
моделей, |
основой |
которых |
являются |
дифференц альные |
уравнения. |
В дифференциальных |
уравнениях |
|
неизвестная функц я содержится вместе со своими производными. Основной задачей теории обыкновенных дифференциальных
уравнен й |
является |
зучение |
функций, |
|
представляющих |
собой |
|||||
решен я эт х уравнен й. |
|
|
|
|
|
|
|
||||
В |
этом |
разделе |
злагаются элементы |
теории обыкновенных |
|||||||
|
|
альных уравнений, когда неизвестная функция зависит от |
|||||||||
одной переменной. |
|
|
|
|
|
|
|
|
|||
дифференц |
|
|
|
|
|
|
|
||||
|
5. ДИФФЕРЕНЦИ ЛЬНЫЕ УР ВНЕНИЯ ПЕРВОГО |
||||||||||
|
|
|
|
ПОРЯДКА |
|
|
|
|
|
||
|
|
|
|
5.1. Основные понятия |
|
|
|||||
Решение |
различных |
прикладных |
задач |
методом |
|||||||
математического моделирования сводится к отысканию неизвестной |
|||||||||||
функции |
из |
уравнения, содержащего |
независимую переменную, |
||||||||
|
|
бА |
|
|
|||||||
искомую функцию и производные этой функции. Такое уравнение |
|||||||||||
называется дифференциальным. |
|
|
|
|
|
|
|
||||
Простейший пример дифференциального уравнения даёт задача |
|||||||||||
о нахождении первообразной |
F(x) для |
заданной функции |
f (x), |
||||||||
|
|
|
|
|
Д |
|
|||||
поскольку её можно рассматривать как задачу о нахождении функции |
|||||||||||
|
|
|
|
|
|
|
f (x). |
|
|
||
F(x), удовлетворяющей уравнению F (x) |
|
|
|||||||||
Дифференциальным уравнением называется уравнение вида |
|||||||||||
|
|
|
|
|
|
n |
|
0, |
|
|
|
|
|
|
|
F x,y, y , ,y |
|
|
|
||||
где x– |
|
независимая |
|
|
y |
|
И |
||||
|
переменная, |
– |
искомая функция и |
||||||||
y , y , |
, y n |
– её производные. |
|
|
|
|
|
|
|
||
Порядком дифференциального уравнения называется |
порядок |
||||||||||
высшей производной, содержащейся в данном уравнении. |
|
|
|||||||||
100
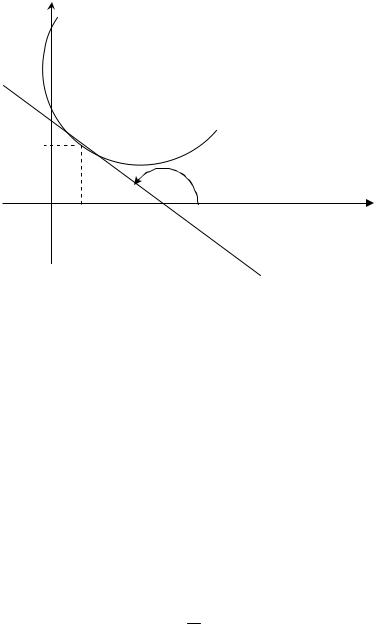
Решением дифференциального уравнения называется всякая функция, которая при подстановке обращает данное уравнение в тождество. Приведем пример, приводящий к дифференциальному уравнению.
Рассмотрим задачу нахождения функции, график которой |
||||
С |
|
|
|
|
обладает тем свойством, что отрезок любой касательной, |
||||
заключенной между осями координат, делится пополам в точке |
||||
касания. |
|
|
|
|
и |
|
|
||
|
y |
|
|
|
бА |
|
|||
|
B |
M |
y f x |
|
|
|
|
|
x |
|
0 |
P |
A |
|
|
|
|
Рис. 5.1 |
|
Пусть y f x – |
|
Д |
||
искомая функция, а M x, y |
– произвольная |
|||
точка кривой, определяемой этим уравнением; предположим для определенности, что кривая расположена в первой четверти (рис. 5.1).
Так как, |
по условию задачи, имеем BM MA, |
то |
OP PA x. |
з |
||||||||
|
|
|
|
|
И |
|||||||
рис. 5.1 |
видно, что |
tg PAM MP |
, т.е. |
tg |
180 |
y |
|
, |
или |
|||
|
y |
|
PA |
|
|
|
|
x |
|
|
||
tg |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
Учитывая, что по геометрическому смыслу производной |
tg |
|||||||||||
есть угловой коэффициент касательной, который |
в точкеM x, y |
|||||||||||
равен y , получаем дифференциальное уравнение |
|
|
|
|
|
|
||||||
y y . x
101
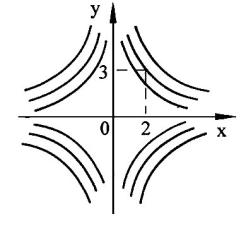
Проверим, |
|
что решением является всякая функция видаy |
C |
, |
|||||||||
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
где C – произвольная постоянная. |
|||||||||||||
Подставляя функцию в уравнение, получим |
|||||||||||||
C |
|
|
C |
|
|
C |
|
C |
|
|
|
||
|
x |
|
, т.е. |
|
. |
|
|
||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
x2 |
x2 |
|
|
|||||||
|
x |
|
|
x |
|
|
|
|
|
|
|||
|
ледовательно, |
равенство |
y |
C |
|
|
|
|
||||||
|
x |
|
|
|
||||||||||
рис |
|
|
|
|
|
|
||||||||
|
функций, |
|
|
|
||||||||||
определяет |
|
множество |
|
|
|
|
||||||||
Собладающ х указанным в задаче |
|
|
|
|||||||||||
свойством. |
Граф ки |
этих |
|
функций |
|
|
|
|||||||
представляют со ой семейство гипербол |
|
|
|
|||||||||||
( |
. 5.2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д фференц альным |
уравнением |
|
|
|
|||||||||
первого порядка называется |
уравнение |
|
|
|
||||||||||
вида |
|
|
|
|
|
|
|
|
|
|
Рис. 5.2 |
|
||
|
F x, y, y 0 |
в неявной форме |
|
|
|
|||||||||
|
|
|
|
|
|
|||||||||
или |
y f (x,y) |
|
|
– разрешённое |
относительно производной, |
или |
||||||||
P(x, y)dx Q(x,y)dy 0 в дифференциальной форме. |
|
|
||||||||||||
|
Рассмотренный |
выше |
|
пример |
показывает, |
что |
||||||||
|
|
|
|
|
|
|
|
Д |
|
|||||
дифференциальное уравнение имеет, вообще говоря, бесконечное |
||||||||||||||
множествобАрешений. |
|
|
||||||||||||
|
Например, непосредственной подстановкой можно убедиться, |
|||||||||||||
что функции |
y 1/ x |
C 1 ; |
|
y 3/ x |
C 3 |
являются решениями |
||||||||
уравнения y |
y |
. |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
Таким образом, каждому дифференциальному уравнению |
|||||||||||||
удовлетворяет бесконечная совокупность его решений. |
|
|
||||||||||||
|
Всякое отдельно взятое решение дифференциального уравнения |
|||||||||||||
называется его частным решением. С геометрической точки зрения |
||||||||||||||
совокупность всех решений дифференциальногоИуравнения |
||||||||||||||
представляет собой семейство кривых, называемых интегральными |
||||||||||||||
кривыми, а каждое частное решение представляет отдельную |
||||||||||||||
интегральную кривую. |
|
|
|
|
|
|
общим |
решением |
||||||
|
Функция |
|
|
y (x,C) |
|
называется |
||||||||
дифференциального уравнения первого порядка, если при любом |
||||||||||||||
значении C эта функция является решением уравнения |
и любое его |
|||||||||||||
102
частное |
решение может |
быть |
получено |
из |
|
общего |
решения |
||||||||||||||||
y x,C при некотором значении постоянной C. |
|
|
|
|
|
|
|||||||||||||||||
В некоторых случаях получают решение дифференциального |
|||||||||||||||||||||||
уравнения в неявной форме, т.е. решение задается формулой вида |
|
|
|
||||||||||||||||||||
С |
|
|
Ф x,y,C 0. |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
общим |
интегралом |
||||||||||||
В этом случае оно называется |
|
||||||||||||||||||||||
дифференциального уравнения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
При решен |
конкретных задач часто необходимо выделить из |
||||||||||||||||||||||
всей совокупности решений дифференциального уравнения то |
|||||||||||||||||||||||
начальнымизаданные ч сла, так е, что при x x0 |
и y y0 функция имеет смысл, |
||||||||||||||||||||||
частное решен е, |
которое является ответом на поставленный вопрос, |
||||||||||||||||||||||
для этого задают так называемое начальное условие. |
|
|
|
|
|
|
|||||||||||||||||
Для |
д фференц ального |
уравнения |
|
первого |
порядка |
под |
|||||||||||||||||
|
|
услов ями для его решения y y x |
понимают условия, |
||||||||||||||||||||
|
бА |
|
,где |
x0 и |
y0 – |
||||||||||||||||||
состоящ е в том, |
что y |
y0 |
при x |
x0 |
, т.е. |
y x0 |
y0 |
||||||||||||||||
т.е. существует |
f x0, y0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Задача нахождения частного решения дифференциального |
|||||||||||||||||||||||
уравнения, удовлетворяющего заданным начальным условиям, |
|||||||||||||||||||||||
называется задачей Коши. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
В случае дифференциального уравнения первого порядка задача |
|||||||||||||||||||||||
Коши формулируется следующим образом: |
найти решение y y x |
||||||||||||||||||||||
|
|
y |
|
|
f x, y , |
|
|
Д |
|
|
|
||||||||||||
уравнения |
|
|
удовлетворяющее при заданных начальных |
||||||||||||||||||||
данных x0, y0 |
начальному условию |
y x0 y0 , где x0, y0– заданные |
|||||||||||||||||||||
числа. |
|
|
|
|
|
|
|
|
|
|
x0 2;y0 3 и требуется найти |
||||||||||||
Пусть даны начальные данные |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|||||||||
частное |
решение |
y y x |
уравнения |
y |
|
|
|
y |
, |
удовлетворяющее |
|||||||||||||
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
C |
|
начальному |
|
|
условию |
y 2 3. |
Подставим |
в |
функциюy |
|
, |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
являющуюся решением данного уравнения, |
начальные данные x 2; |
||||||||||||||||||||||
y 3. Получаем, |
что 3 C /2, |
т.е. |
C 6. |
|
Таким образом, |
искомым |
|||||||||||||||||
частным решением уравнения является функция y 6/ x. Геометрически решение, удовлетворяющее начальному условию
y x0 y0 , представляет интегральную кривую, проходящую через данную точку x0, y0 .
103
