
1697
.pdf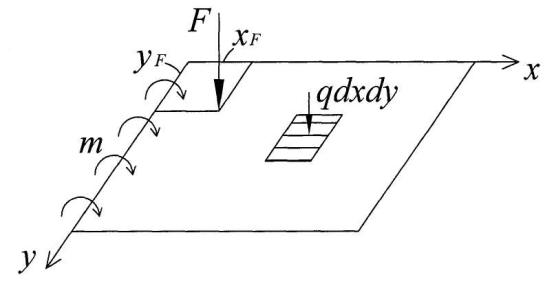
В.Н. ЗАВЬЯЛОВ, Е.А. МАРТЫНОВ,
В.М. РОМАНОВСКИЙ
ОСНОВЫ
СТРОИТЕЛЬНОЙ МЕХАНИКИ
ПЛАСТИН
Учебное пособие
Омск 2012
Министерство образования и науки РФ Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования «Сибирская государственная автомобильно-дорожная академия (СибАДИ)»
В.Н. ЗАВЬЯЛОВ, Е.А. МАРТЫНОВ,
В.М. РОМАНОВСКИЙ
ОСНОВЫ СТРОИТЕЛЬНОЙ МЕХАНИКИ ПЛАСТИН
Учебное пособие
Издание второе, исправленное
Омск
СибАДИ
2012
2
УДК 624+539. 3 ББК 38.112
О93
Рецензенты:
д-р физ.-мат. наук, проф. Т.А. Ковалевская, зав. каф. "Теоретическая механика" ТГАСУ; д-р техн. наук, проф. С.А. Макеев,
зав. каф. "Строительные конструкции" СибАДИ
Работа одобрена редакционно-издательским советом академии в качестве учебного пособия.
Основы строительной механики пластин: учебное пособие /В.Н.
Завьялов, Е.А. Мартынов, В.М. Романовский. – 2-е изд., испр. – Омск: СибАДИ, 2012. – 116 с.
В настоящем учебном пособии изложены принципиальные основы расчёта прямоугольных пластин, работающих как в упругой, так и в упругопластической стадиях, при различных видах их деформирования. Кроме того, в пособии представлен в необходимом для расчёта пластин объёме математический аппарат, связанный с различными методами вариационного исчисления. Приведены примеры расчёта пластин методом конечных элементов.
Данное учебное пособие рекомендуется студентам, занимающимся научно-исследовательской работой, студентам-дипломникам и аспирантам строительных специальностей.
Табл. 3. Ил. 45. Библиогр.: 31 назв.
ФГБОУ ВПО «СибАДИ», 2012
3
ОГЛАВЛЕНИЕ
Предисловие…..…...……………………………………………………… 4
1.Напряженно-деформированное состояние в пластинах …….…… 5
1.1.Основные понятия и гипотезы ………………………….…………. 5
1.2.Определение перемещений и деформаций …………………….…. 7
1.3.Напряжения в пластинах ……………………………………..……. 9
1.4.Определение внутренних усилий и напряжений…………………. 11
2.Дифференциальное уравнение изогнутой поверхности пластины …………………………………………………………….…. 16
2.1.Уравнения равновесия элемента пластины …………….……….… 16
2.2.Основные дифференциальные уравнения изгиба пластины ….…. 18
2.3.Граничные условия на контуре пластины ……………….……….. 19
2.4.Изгиб шарнирно опертых прямоугольных пластин ……………… 25
3.Вариационные методы расчета прямоугольных пластин ………. 32
3.1.Основные понятия вариационного исчисления ………………….. 32
3.2.Полная энергия деформации при изгибе пластин ………….…….. 34
3.3.Вариационное уравнение изгиба пластины ………………………. 36
3.4.Метод Ритца ………………………………………………………… 42
3.5.Метод Бубнова-Галеркина ……………………………….………... 48
3.6.Метод Канторовича-Власова ……………………………………… 55
3.7.Метод конечных элементов ………………………………..…..…... 60
3.8.Пример расчета пластины, работающей в упругой стадии, методом конечных элементов ………………………………..……. 67
4.Устойчивость прямоугольных пластин …………………………… 80
4.1.Пластины при совместном действии поперечной нагрузки и нагрузки в срединной плоскости ……………………... 80
4.2.Устойчивость шарнирно опертых прямоугольных пластин при равномерном сжатии в одном направлении ……………….… 83
4.3.Устойчивость свободно опертой пластины, сжатой в двух направлениях ……………………………………………………….. 86
4.4.Устойчивость прямоугольных пластин при сдвиге …...…………. 89
5.Изгиб прямоугольных пластин за пределом упругости …….…… 94
5.1.Основные положения и гипотезы ………..…………………….…. 94
5.2.Уравнения упругого пластического изгиба пластины ……….….. 98
5.3.Расчет пластин за пределом упругости методом конечных разностей …………..………………………………………….……. 102
5.4.Решение упругопластических задач при изгибе пластин вариационным методом ……………………………………………. 104
5.5.Расчет пластин за пределом упругости методом конечных
элементов ………………………………………………….…….….. 107 Библиографический список………………………….……………….... 114
4
ПРЕДИСЛОВИЕ
Строительство является той отраслью деятельности промышленного комплекса, которая всегда была, есть и останется востребованной хозяйством страны.
Одним из важных элементов конструкций как транспортных, так и других строительных сооружений являются различного вида пластины. Поэтому вопросы, связанные с теоретическими исследованиями работы пластин, остаются актуальными.
Предлагаемое вниманию читателей учебное пособие посвящено основным проблемам расчёта пластин, работающих как в пределах закона Гука, так и в упругопластической стадии.
Сначала приведены классические определения пластины и выделен класс пластин, рассматриваемых в данном пособии. Приведены гипотезы, принятые при расчётах таких пластин, а также классические уравнения теории упругости, на базе которых и ведутся дальнейшие теоретические обоснования тех или иных методов расчёта и применяются эти методы на конкретных примерах.
Представляет интерес раздел, в котором в концентрированном виде описаны вариационные методы расчёта прямоугольных пластин. Представлен пример расчёта пластины, работающей в упругой стадии, выполненный современным методом конечных элементов.
В пособии имеется раздел, посвящённый некоторым аспектам расчёта пластин на устойчивость. При этом рассмотрено несколько наиболее характерных условий закрепления пластин.
Особое внимание уделено расчёту пластин, работающих за пределом упругости. Теоретические обоснования такого расчёта подкреплены числовым примером.
Пособие предназначено для студентов-дипломников, аспирантов и практических инженеров, в чью сферу профессиональной деятельности входят рассматриваемые вопросы.
5
1.НАПРЯЖЕННО-ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ
ВПЛАСТИНАХ
1.1. Основные понятия и гипотезы
Пластиной называют тело, имеющее форму прямой призмы или цилиндра, высота которого значительно меньше размеров основания.
В зависимости от формы основания различают круглые, эллиптические, прямоугольные, треугольные и подобные пластины. В данном пособии рассматриваются только прямоугольные пластины, получившие наибольшее распространение в строительстве различных сооружений.
Плоскость, которая делит высоту пластины пополам, называется
срединной плоскостью.
Линии пересечения срединной плоскости с боковой поверхностью образуют контур пластины.
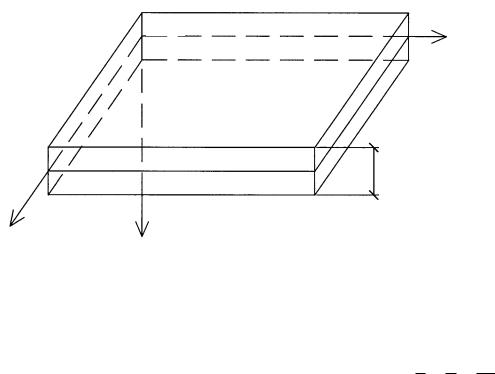
Координатную плоскость xoy будем считать совпадающей со срединной плоскостью пластины (рис. 1.1). Ось z направим вниз, считая прогибы пластины положительными, если они направлены вниз. Под прогибами пластины w подразумеваем перемещения в вертикальном направлении точек срединной поверхности.
x
0
h
y
z
Рис. 1.1
Толщина пластины оказывает влияние на ее свойства при изгибе. Различают три вида пластин в зависимости от отношения толщины к наименьшему размеру в плане.
1. Тонкими (жесткими) называются пластины, у которых 1 h 1 . 5 b 80
6

2. Пластины, у которых прогиб w более h , называются гибкими.
4
3. Пластины, у которых h 1, называются толстыми плитами. b 3
Толстые пластины (плиты) рассчитываются с помощью решения основных уравнений трехмерной теории упругости.
Тонкие пластины в зависимости от вида напряженного состояния разделяются на:
1.Жесткие пластины, при изгибе которых можно пренебречь напряжениями в срединной плоскости.
2.Пластины конечной жесткости (гибкие пластины), у которых величины изгибных напряжений и напряжений в срединной плоскости одного порядка.
3.Абсолютно гибкие пластины, у которых учитываются только напряжения в срединной плоскости.
Поскольку толщина пластины мала по сравнению с размерами в плане, можно пренебречь некоторыми факторами и ввести гипотезы, упрощающие теоретические выводы.
Эти допущения аналогичны тем, которые сделаны в теории изгиба балок и равносильны пренебрежению факторами, мало влияющими на напряженно-деформированное состояние в пластинах.
1.Любой линейный элемент, нормальный к срединной плоскости пластины до ее деформирования, остается прямолинейным и длина его не изменяется после деформирования:
z 0.
(1.1)
2. Любой линейный элемент, нормальный к срединной плоскости до деформирования пластины, остается нормальным к срединной плоскости после деформирования, т.е. угловые относительные деформации
yz 0; xz 0.
(1.2)
3. В срединной плоскости деформации растяжения, сжатия и сдвига равны нулю, а следовательно, перемещения в срединной плоскости вдоль осей x и y отсутствуют:
u0 0; 0 0.
(1.3)
7
4. Напряжение z мало по сравнению с x и y , т.е. давлением слоев вдоль оси z пренебрегаем:
z 0.
(1.4)
Приведенные гипотезы (допущения) справедливы только для тонких пластин.
1.2. Определение перемещений и деформаций
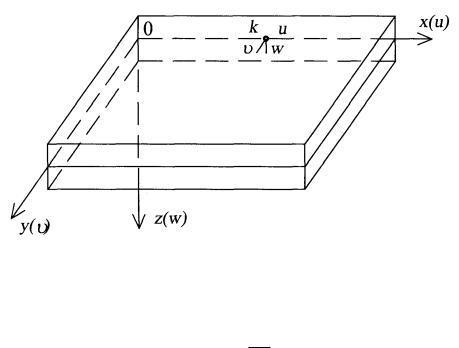
Исследуем пластину, загруженную поперечной нагрузкой, нормальной к срединной плоскости. Под действием такой нагрузки каждая точка k пластины (рис. 1.2) получает перемещения u x, y,z , x, y,z , w x, y,z соответственно вдоль осей x, y, z.
Рис. 1.2
Согласно первой гипотезе имеем
w
z z 0.
(1.5)
Принятая гипотеза позволяет сделать вывод о том, что перемещение w x, y,z будет функцией только координат x, y, т.е. все точки, лежащие на перпендикуляре к срединной плоскости, будут иметь одинаковые прогибы. Это позволяет, определив перемещения w для точек срединной поверхности, определять прогибы для всех точек нормали, лежащих на ней.
8
Согласно геометрическим соотношениям Коши [1] и второй гипотезе
|
|
|
u |
|
|
w |
|
|
||
|
xz |
|
|
|
|
0; |
||||
|
|
|
||||||||
|
|
z |
|
x |
||||||
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w |
|
|||
|
|
|
|
|
||||||
|
|
|
|
|
|
0, |
||||
|
yz |
|
|
|
||||||
|
|
z |
|
|
y |
|||||
|
|
|
|
|
||||||
(1.6)
отсюда
|
u |
w |
||||||
|
|
|
|
|
|
; |
||
|
|
|
||||||
|
z |
|
x |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w |
|
|||
|
|
|
. |
|||||
|
|
|||||||
|
z |
|
y |
|||||
|
|
|||||||
(1.7)
Интегрируя эти уравнения по z, получим
|
w |
|
|
|
|
|
|
u z |
|
f |
1 |
(x, y); |
|||
|
|||||||
|
x |
|
|
||||
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w |
|
|
|
|||
|
f2(x, y). |
||||||
|
|
|
|||||
z |
|
|
|||||
|
y |
|
|
|
|||
|
|
|
|
||||
(1.8)
Согласно третьей гипотезе
при z 0; u 0; 0 f1(x, y) 0; f2 (x, y) 0.
Перемещения u, принимают вид
|
w |
||
u z |
|
; |
|
|
|||
|
x |
||
|
(1.9) |
||
|
w |
||
|
|
|
|
z . |
|||
|
y |
||
|
|||
9
Относительные линейные и угловую деформации для произвольной точки пластины определяем по формулам Коши:
|
|
|
u |
|
|
z |
|
2 |
w |
|
; |
|
|
|||||||
x |
|
|
|
|
|
|
|
|||||||||||||
|
x |
x2 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
2 |
w |
|
|
|
|||||||
|
|
|
|
z |
|
|
; |
|
|
|||||||||||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
y |
y2 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
2w |
|
||||
|
|
|
|
|
|
2z |
||||||||||||||
|
xy |
|
|
. |
||||||||||||||||
|
|
|
|
y |
|
x |
|
|
|
|
|
|
x y |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
(1.10)
Полученные формулы показывают, что для точек срединной поверхности (z = 0) деформации x, y , xy равны нулю.
1.3. Напряжения в пластинах
Для определения напряжений используем закон Гука для плоской задачи теории упругости. Поскольку согласно четвертой гипотезе z 0, то
|
|
|
|
1 |
|
|
|
|
|
|
; |
|
|
|||
|
x |
|
|
|
|
|
x |
|
y |
|
|
|||||
|
|
|
|
|
||||||||||||
|
|
|
E |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
|
y |
x ; |
|
|
|||||||
y |
|
|
|
|
|
|||||||||||
E |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
21 |
|
|
|
||||
|
|
|
|
|
|
xy |
|
|
|
|
|
. |
||||
|
xy |
|
|
|
|
|
|
|
xy |
|||||||
|
|
|
|
|
||||||||||||
|
|
|
|
G |
|
|
E |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Решая полученную систему уравнений, находим
|
|
|
|
E |
|
|
|
|
|
|
|
; |
||
|
x |
|
|
|
|
|
x |
|
y |
|||||
|
|
|
||||||||||||
|
|
1 2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
E |
|
|
y x ; |
|||||||
y |
|
|
|
|
|
|||||||||
1 |
2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
хy |
|
|
|
|
|
|
xy |
. |
|
|
|||
|
|
|
|
|
|
|
||||||||
|
|
|
21 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
10 |
|
|
|
|
|
|
|
|
|
|
||
(1.11)
(1.12)
