1697

(5.28)

В упругопластическом состоянии пластины после получения с (границы раздела упругой и пластической зон по толщине пластины) в разных точках можно получить границы пластических зон на поверхности пластины между точками.

5.3. Расчет пластин за пределом упругости методом конечных разностей

111

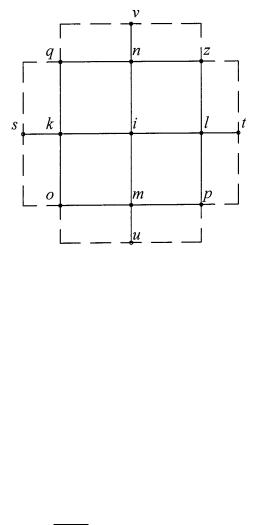
При расчете методом конечных разностей пластину мысленно покрываем сеткой с шагом x y . Уравнение (5.19) запишем в конечных разностях. Для i узла (рис. 5.4) это уравнение принимает вид

20wi 8 wk wl wn wm 2 w0 wp wq wr

(5.29)

Рис. 5.4

Уравнение (5.29) приведено в [18].

Решая систему уравнений (5.29), находим значения прогибов в узлах сетки wi, …, wu .

Изгибающие и крутящие моменты в узлах находим

Мxi 21 v wi wк wl v wm wn ;М yi 21 v wi wm wn v wк wl ;

(5.30)

112

Используя условие Губера-Мизеса, определяем нагрузку при появлении текучести в узлах пластины, полагая z h .

Имея значения i в узлах сетки, определяем интерполяцией границы пластических зон на поверхности пластины.

Зная i , определяем пластические коэффициенты i, зависящие от пластических зон и вида диаграммы i i . Для диаграммы (см. рис. 5.2) получаем

(5.33)

Правые части уравнений (5.29) принимают вид

Ki 1 2 Mxi M yi i Mxk k Mxi i M ym m

(5.34)

Решаем систему линейных уравнений (5.29) при найденных Ki и находим значения упругопластических прогибов wi, …, wp в первом приближении.

113

Количество последовательных приближений зависит от разности значений i двух соседних приближений. Расчеты пластин за пределом упругости методом конечных разностей приведены в [18] для разных условий опирания пластин и при разных диаграммах деформирования материала i i .

5.4.Решение упругопластических задач при изгибе пластин вариационным методом

Расчет пластин за пределом упругости проводится вариационными методами, основанными на принципе минимума полной энергии пластины, состоящей из потенциальной энергии деформации и потенциала внешних нагрузок. Функции прогибов, доставляющие минимум полной энергии, находятся либо путем прямой минимизации функционала [28], либо путем решения систем линейных уравнений, правая часть которых зависит от глубины пластических деформаций по толщине пластины.

Применение энергетических методов к решению упругопластических задач нашло в работах [24], [26].

Зависимость между G и переменным (секущим) модулем сдвига принимаем в виде

G G ,

(5.35)

где G i – функция пластичности, которая определяется физическими ii

свойствами материала.

Работу внутренних сил представим как сумму работ по изменению объема и формы и применим принцип минимума полной энергии пластины

(5.36)

где V – объем пластины; A – площадь пластины.

Поскольку функция пластичности зависит от искомой функции прогибов, то энергетический функционал получается неквадратичным.

В работе [30] минимум неквадратичного функционала определялся методом сопряженных градиентов.

114

В работах [18] получено квадратичное выражение функционала путем замены функции пластичности в k-м приближении ее значением в k– 1 приближении:

k k 1.

(5.37)

Тогда энергетический функционал становится квадратичным:

(5.38)

Коэффициент поперечной деформации через функцию пластичности представим в виде

(5.39)

Энергия изменения объема выражается

(5.40)

Выражение для i :

1 v' v'2

1 31 v' 2 .

(5.41)

Работу по изменению формы для k-го приближения получаем в виде

115

(5.42)

Суммируя Э0 и VK , получаем уравнение для упругопластического изгиба пластин:

Искомая функция прогибов задается в виде ряда

n

w x, y CK wK ,

K 1

(5.44)

где wK – функции, удовлетворяющие геометрическим условиям

пластическая функция, интегрально учитывающая размягчение материала по толщине пластины.

116

Выражение D K 1 характеризует переменную жесткость пластины в k-м приближении.

Нулевым приближением решения является расчет в упругом состоянии, при этом функция пластичности принимается равной единице.

При заданном значении внешней нагрузки находится величина , которая подставляется в уравнение (5.45), и находится величина прогибов пластины в первом приближении w. Расчет продолжается до тех пор, пока разность между решениями двух последних приближений не достигнет заданной величины.

5.5. Расчет пластин за пределом упругости методом конечных элементов

Выражение, описывающее изгиб срединной поверхности пластины, работающей в упругопластической стадии, соответствует дифференциальному уравнению (5.19). В этом уравнении величины внутренних усилий с верхним индексом у определяются с применением известных классических уравнений (1.28), (1.29), (1.32), (1.33), (1.37)

расчета пластин с использованием в рассматриваемой методике аппроксимирующей функции (3.96), выраженной через найденные с помощью МКЭ перемещения Zi. Эти формулы представлены на стр. 77 и 78 настоящего пособия.

На рис. 3.19 показаны значения внутренних усилий (Мху и М уу ),

полученных при упругом расчете МКЭ, рассмотренном в настоящем пособии.

Параметр , соответствующий диаграмме Прандтля, принят согласно выражению (5.33). Параметры, входящие в выражение (5.33), показаны на

рис. 5.3. При этом безразмерный параметр 2с. h

Для анализа развития пластических деформаций была принята гипотеза Губера-Мизеса (5.20).

Из рис. 3.19 видно, что наибольшие значения внутренних усилий для рассматриваемой схемы загружения пластины имеют место в срединах защемленных граней. Именно в этих точках и должны в первую очередь появиться пластические деформации. Для оценки напряженного состояния пластины имеет значение не только нагрузка текучести qe, но и так называемая предельная нагрузка qпр , при которой по всей высоте опасного

сечения происходит развитие пластических деформаций.

117

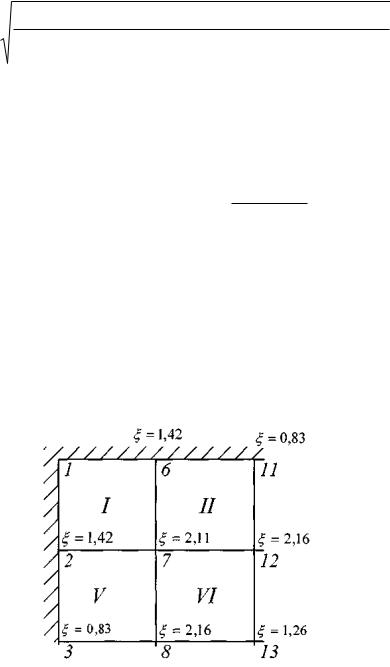
Эта величина определяется также из выражения (5.22) при замене в правой части момента сопротивления Wz на пластический момент сопротивления We . В рассматриваемом примере наименьшие значения этих нагрузок оказались следующими: qe 5,84кг/см2 и qпр 8,76 кг/см2.

В дальнейшем расчет предполагает определение как размеров зон текучести в плане, так и размеров развития пластических деформаций по высоте сечения. Последнее легко определить из (5.22), если задавать значение q в пределах: qпр q qe . Если, например, задать q = 1,2qe , то

деформаций целесообразно перейти к безразмерному параметру i , определяемому из выражения

i e We ,

1,2q Фi

(5.47)

где Фi квадратный корень из выражения в квадратных скобках в (5.46) для i - го стыка конечного элемента.

Если величина i 1, это свидетельствует о том, что в данном узле имеет место развитие пластических деформаций. На рис. 5.5 показано поле значений параметров i для четверти рассматриваемой пластины.

118

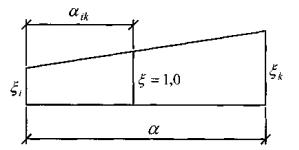
Рис. 5.5

Из анализа представленных значений параметров i видно, что вслед за развитием пластических деформаций в серединах защемленных граней произойдет развитие пластических деформаций в середине пластины.

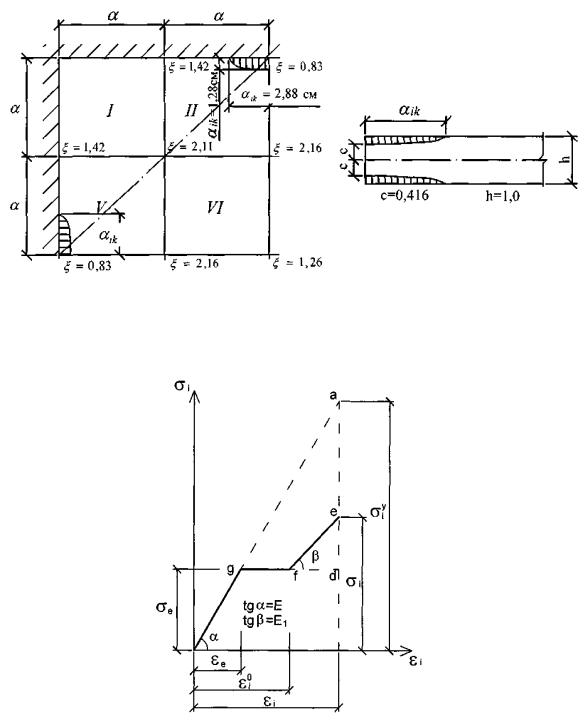
Для определения размеров в плане зон развития пластических деформаций использовалась прямая пропорциональная зависимость между параметрами i для соседних узлов стыков конечных элементов. В соответствии с этим находилась величина aik , представляющая длину прямой, соединяющей рассматриваемые соседние узлы. Величина aik в соответствии с этим может быть найдена из выражения

(5.48)

На рис. 5.6 показана схема определения aik , где i и k – соответственно узел и точка определения зоны пластичности.

Рис. 5.6

Определив параметры i в узлах, определяем в рассматриваемом примере (диаграмма Прандтля) по (5.33) пластические коэффициенты i.

При найденных для каждого узла стыков конечных элементов значенияхi определяем правую часть уравнения (5.19). По предлагаемой методике это соответствует формированию глобального вектора свободных членов системы алгебраических уравнений по определению Zi. Решая эту систему, находим на каждом шаге итерации новые величины упругопластических w прогибов в узлах пластины. Количество последовательных приближений определяется из условия, чтобы разность между двумя последующими значениями i для контролируемого узла не превышала заранее заданной точности. При нагрузке q = 1,2qe на рис. 5.7 показаны зоны пластичности

119

как в плане по поверхности пластины, так и по высоте сечения, расположенного в середине защемленной грани [27].

Рис. 5.7

Рассмотрим теперь решение этой задачи для диаграммы напряжений, имеющей площадку текучести (рис. 5.8) и упрочнение материала, происходящего по линейному закону.

Рис. 5.8

По деформационной теории функция пластичности на площадке текучести gf может быть описана выражением

120