
1697
.pdf
|
a |
|
D 4 |
|
|
|
|
|
|||
Обозначим |
|
|
; |
|
. |
Тогда уравнение |
(4.33) |
||||
|
|
|
|||||||||
|
b |
|
32 b2Txy |
|
|
|
|
|
|||
примет вид |
|
|
|
|
|
|
|
|
|||
|
|
|
m2 n2 |
2 2 |
mnpq |
|
|
|
|
||
Amn |
|
Apq |
|
|
|
0. |
(4.34) |
||||
2 |
m2 p2 q2 |
n2 |
|||||||||
|
|
|
p q |
|
|
||||||
Получили систему линейных однородных уравнений относительно параметров Amn . Для нахождения Txy приравняем определитель из
коэффициентов при Amn нулю. В связи с тем, что число уравнений бесконечно, точное решение будет получено, если раскрыть определитель с бесконечным числом строк и столбцов. Приближенное решение можно получить, взяв конечное число параметров Amn .
Учитывая два параметра A11 и A22 , получаем выражения
1 2 2 |
|
|
4 |
|
|
|
||
|
|
|
|
|
|
|
|
|
2 |
A11 9 A22 0; |
|||||||
|
||||||||
|
16 1 2 |
2 |
|
|
|
|
|
|
|
A |
|
4 |
A 0. |
||||
|
|
|
|
|||||
2 |
|
22 |
|
|
9 |
11 |
||
|
|
|
|
|
|
|||
(4.35)
Приравняем нулю определитель системы (4.35):
|
1 2 2 |
4 |
|
|
|
|
|
|
|||||
|
|
2 |
|
9 |
|
0. |
|
|
|
||||
|
|
4 |
|
16 1 2 2 |
|
|
|
||||||
|
|
9 |
|
|
2 |
|
|
(4.36) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
Раскрывая определитель (4.36), находим |
|
|
|
. |
|||||||||
9 |
1 2 2 |
||||||||||||
Учитывая выражение , получаем
101
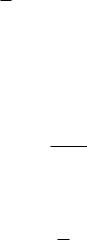
Txy |
|
9 4D |
|
1 2 2 |
. |
|
|
32b2 |
|
|
|
||||
кр |
|
|
3 |
|
(4.37) |
||
|
|
|
|
|
|
|
|
Знаки плюс и минус указывают на то, что значение критических сил |
|||||||
не зависит от их направления. |
приближенное значение Txy |
|
|
||||
Выражение (4.37) дает |
с |
||||||
|
|
|
|
|
|
кр |
|
погрешностью около 10 % для квадратных пластин и с еще большей
погрешностью при других отношениях a . b
Чтобы получить более точный результат, следует учитывать большее число параметров Amn . Так, если учитывать шесть параметров: A11, A22 , A13 , A31, A33, A42 , то критическое усилие оказывается равным
Txy кр K b22D ,
(4.38)
где K – постоянная, зависящая от отношения a . Значения K приведены в
табл. 4.1 для различных . |
|
|
b |
|
|
|
|||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
Таблица 4.1 |
|
|
|
|
|
|
|
|
|
|
|
|
1,0 |
1,2 |
1,4 |
1,5 |
1,6 |
1,8 |
2,0 |
2,5 |
3,0 |
K |
9,4 |
8,0 |
7,3 |
7,1 |
7,0 |
6,8 |
6,6 |
6,3 |
6,1 |
102
5.ИЗГИБ ПРЯМОУГОЛЬНЫХ ПЛАСТИН ЗА ПРЕДЕЛОМ УПРУГОСТИ
5.1. Основные положения и гипотезы
При изучении прямоугольных пластин за пределом упругости используют теорию пластичности, в которой рассматриваются и условия работы пластины, и свойства материала.
Решение задач изгиба пластин за пределом упругости может быть получено в предположении выполнения принципа простого нагружения. А.А. Ильюшин [12] назвал простым нагружением такой процесс, при котором все приложенные к телу усилия возрастают пропорционально одной и той же величине. При этом тензор напряжений в каждой точке пропорционален тензору деформаций. Доказано, что если тело до нагружения было изотропным и нагружение простое, то неупругое поведение пластин описывается теорией малых упругопластических деформаций.
Для описания неупругого деформирования пластин широкое применение находят две теории – деформационная теория пластичности и теория пластического течения.
Деформационная теория устанавливает связь между деформацией и напряжением, а также только начальное и конечное напряженнодеформированное состояние. Эта теория основана на двух законах, определяющих процесс активной деформации и процесс разгрузки.
Теория течения устанавливает зависимость между напряжениями и скоростями деформаций, предполагая пластическую деформацию как процесс движения, т.е. пластическая деформация оказывается зависящей от пути нагружения.
Пределы применимости деформационной теории и теории пластического течения определяются опытным путем.
При расчете пластин за пределом упругости в основном применяется разновидность деформационной теории – теория малых упругопластических деформаций.
В основе этой теории справедливы гипотезы:
1)объемная деформация пропорциональна среднему напряжению;
2)направляющие тензора напряжений и тензора деформаций совпадают;
3)интенсивность напряжений является функцией интенсивности деформаций, не зависящей от вида напряженного состояния.
Принятые гипотезы справедливы в случае простого нагружения, при котором направляющие тензора напряжений в каждой точке постоянны.
103
В случае однородного напряженного состояния тела нагружение будет простым при пропорциональном увеличении всех внешних нагрузок, а диаграмма "напряжения – деформация" описывается функцией
i A im ,
(5.1)
где i , im – интенсивности напряжений и деформаций; A – постоянная величина.
Зависимость между параметром внешних сил m, напряжений и деформаций определяется
|
1 |
|
Pij |
|
ij |
|
||
m ; |
|
. |
||||||
P0 |
|
|||||||
|
|
|
|
0 |
|
|||
|
|
|
ij |
|
|
ij |
||
(5.2)
Приведенной зависимостью (5.1) могут описываться кривые i i материалов, работающих в пластической области. При m 0 имеем упругопластический материал. Соотношения теории малых упругопластических деформаций выполняются для материалов с разными диаграммами i i при активной пластической деформации в каждой точке тела.
Согласно деформационной теории различие в физических уравнениях для пластических и нелинейно-упругих тел проявляется лишь при рассмотрении процесса разгрузки. Физические соотношения между напряжениями и деформациями имеют вид
x ñð 2G x ñð ; |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
y |
ñð |
2G |
|
y |
ñð |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
; |
|
|
|
(5.3) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
z |
|
ñð |
|
|
|
|
z |
|
|
ñð |
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
, |
|
|
|
, |
|
|
xy |
G |
xy |
xz |
G |
xz |
yz |
G |
yz |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
где x , y , z , yz; x , y , z , yz – компоненты напряжений и деформаций; ср, ср – средние напряжения и деформации;G – модуль сдвига.
104

|
|
|
|
|
G |
i |
; ср |
1 |
x y z ; ср |
|
1 |
|
x |
y z . |
|
|
|
(5.4) |
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
i |
|
|
|
|
|
|||||||||||||||
|
1 |
|
|
|
|
|
|
3 |
3 |
|
|
|
|
|
|
||||||||||
xy |
|
|
|
|
|
x |
y 2 y z 2 x z 2 6 xy2 xz2 yz2 . |
(5.5) |
|||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
6 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
i |
|
2 |
|
|
|
x y 2 y z 2 x z 2 |
|
3 |
xy2 |
xz2 yz2 |
. |
(5.6) |
|||||||||||||
3 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||
Если известна диаграмма i i , то устанавливается зависимостьi Е i , в которой Е – переменный модуль деформации.
Тогда i и i выражаются
Е 21 G ; |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
|
|
i |
3; |
i |
|
i |
|
|
|
|
, |
||
|
|
|
|
||||||||||
|
i |
|
|
|
|
21 |
|
||||||
|
|
|
|
|
|
|
|
|
|
||||
(5.7)
где – коэффициент поперечной деформации, равный 0,5. Переменный модуль деформации выражается через модуль
упругости
Е Е 1 ,
(5.8)
где носит название функции пластичности. Из уравнений (5.3) находим
|
|
|
|
1 |
|
|
|
|
3 |
|
|
|
|
|
|
1 |
|
|
|
|
||||||
|
x |
|
|
|
|
|
x |
|
|
|
|
|
|
ср |
; |
|
xy |
|
|
|
|
|
|
xy |
; |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
2G |
|
|
1 |
|
|
|
|
G |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
1 |
|
|
|
|
|
3 |
|
|
; |
|
|
|
|
1 |
|
|
|
|
||||
|
y |
|
|
y |
|
|
|
|
|
|
xz |
|
|
|
|
|
xz |
; |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
1 |
ср |
|
|
|
|
G |
|
|||||||||||
|
|
|
|
2G |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
1 |
|
|
|
|
3 |
|
|
|
|
|
|
1 |
|
|
|
|
||||||
z |
|
|
|
z |
|
|
|
|
|
ср |
; |
yz |
|
|
|
|
yz . |
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
2G |
|
|
|
1 |
|
|
|
|
|
G |
|
|
||||||||||
(5.9)
Зависимость между средним напряжением и средней деформацией выражается с помощью К – модуля всестороннего сжатия.
105
|
ср К ср; |
|
К |
2G 1 |
. |
|
|
|||||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
2 |
(5.10) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Полагая z 0; |
xy 0; |
yz |
|
0, получаем выражения для |
||||||||||||||||
определения напряжений в пластине: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
Е |
|
x |
|
y |
|
|
|
|
|
|||||||
|
|
x |
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
Е |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
y |
x |
|
|
|
|
|
|||||||||
|
|
y |
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
Е |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
x |
y |
|
. |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
xy |
|
2 1 |
|
|
|
|
xy |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.11) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Из выражений (5.7), (5.8), (5.10) и (5.11) получаем |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
' |
|
1 2 . |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
(5.12) |
|
2 |
|
||||||||
Пределы значения получим при |
|
|
|
|
|
|
||||||||||||||
1, равном 0,5. |
||||||||||||||||||||
В упругопластическом состоянии пластины в наиболее напряженном сечении возникают пластические деформации. Условие, соответствующее появлению текучести, называется критерием текучести. Это условие может формулироваться по-разному. Условие текучести выполняется при следующих допущениях:
1.Элемент пластины испытывает только активные деформации, при этом эффект Баушингера отсутствует.
2.Условие текучести может быть выражено через напряжение. Это условие не зависит от пути напряжения.
3.Материал предполагается изотропным.
4. Среднее напряжение ср не оказывает влияния на условие
текучести.
Условие текучести в общем виде записывается
f Sij Ke; ,i, j x, y,z ,
(5.13)
где K – критерий текучести; Sij – компоненты девиатора напряжений.
106
М. Губером и Р. Мизесом в качестве критерия текучести принято условие постоянства потенциальной энергии упругого изменения объема
i T .
(5.14)
Для пластин это условие имеет вид
i2 x2 2y x y 3 xy2 T2.
(5.15)
5.2. Уравнения упругого пластического изгиба пластины
Расчет прямоугольных пластин в упругопластической стадии проводится на основании деформационной теории пластичности с использованием метода упругих решений.
Рассмотрим дифференциальные уравнения равновесия в моментах (2.5) и (2.6) для элемента пластины (рис. 5.1).
x
y
Рис. 5.1
Изгибающие и крутящие моменты для упругопластического состояния на основе метода упругих решений [18] можно представить
М x М xy М x0; М y М yy М 0y ; H H y H 0 ,
(5.16)
107
где М xy , М yy , H y – моменты при упругом решении, описанные выражениями (1.28), (1.29) и (1.37); М x0 , М y0, H 0 – моменты от разности
напряжений, изменяющихся по упругому и неупругому законам в пластических областях пластин.
Эти моменты зависят от вида диаграммы i i материала и
определяются
М x0 М xy x; М y0 М yy y ; H 0 H y xy .
(5.17)
С учетом изложенного получается выражение
2М xy |
|
2М yy |
2 |
2H 2 |
q |
2 |
М x0 |
||
x2 |
y |
2 |
x y |
x2 |
|||||
|
|
|
|||||||
Подставляя в (5.18) выражения (5.17), получаем
|
4w |
|
4w |
|
4w |
1 |
|
2 М xy x |
|
2 М yy y |
|||||||
|
|
2 |
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
x2 |
y |
|
|
|||||||
x4 |
y2 |
y4 |
D |
|
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2М y0 |
|
|
2H 0 |
||
|
|
|
2 |
|
|
. |
y |
2 |
|
|
|||
|
|
x y |
||||
|
|
|
|
|
(5.18) |
|
|
2 H y xy |
|
|
2 |
|
|
.(5.19) |
x y |
|
||
|
|
|
|
|
|
|
|
Уравнение (5.19) упругопластического деформирования пластины в перемещениях отличается от уравнения (5.18) в упругом состоянии дополнительными слагаемыми в правой части, зависящими от распространения зон текучести.
Для определения границ пластических деформаций на поверхности и по толщине пластины используем условие пластичности Губера-Мизеса
x2 2y x y 3 xy2 е2 .
(5.20)
Упругие напряжения определяются
108
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E z |
|
|
|
M xy |
|
|
Mxy |
z |
|
|
|
M xy |
z |
|
|
M xy |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
h3 |
|
|
|
|
|
h |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
Wz |
|
|
|
Wz |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M y |
|
|
M y |
z |
|
|
|
M y |
z |
|
|
M y |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E z |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
y |
|
|
|
y |
|
|
|
|
|
y |
|
|
|
|
|
|
y |
|
; |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
D |
|
|
|
h3 |
|
|
|
|
|
|
|
h |
|
|
|
Wz |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Wz |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
xy |
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Wz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.21) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 h |
2 |
|
|
|
|
|
2z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где Wz |
|
|
; |
|
|
|
|
|
|
определяют границу упругой и пластической зон |
|||||||||||||||||||||||||||||||||||
|
|
|
|
h |
|
||||||||||||||||||||||||||||||||||||||||
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
по толщине пластины. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Условие пластичности (5.20) с учетом (5.21) принимает вид |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
z |
2 |
|
|
|
|
|
|
|
|
y |
2 |
|
|
|
|
|
y |
2 |
|
y |
|
y |
|
|
|
|
y |
2 |
|
2 2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
Mx |
|
|
M y Mx |
|
M y |
3 H |
|
|
eWz . |
|||||||||||||||||||||||||
|
|
|
1 |
|
|
|
2 |
|
|
||||||||||||||||||||||||||||||||||||
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(5.22)
Заменяя моменты нагрузкой, определяем расстояние с границы упругой зоны от срединной поверхности пластины в рассматриваемом сечении (узле):
|
2z |
|
2c |
e Wz |
|
|
|
|
|
|
|
|
|
; |
(5.23) |
h |
|
a Ф |
|||||
|
|
h |
|
|
|||
Ф Mx2 M y2 |
MxM y 3H 2 , |
(5.24) |
|||||
где a q dxdy (для случая действия распределенной нагрузки на пластину).
Нагрузка, при которой появляется текучесть в данном узле, определяется из условий
с |
h |
qe |
e |
Wz |
|
|
|
; 1; |
|
|
. |
||
2 |
|
Ф |
||||
|
|
|
|
|
||
(5.25)
109
Зная нагрузки текучести для нескольких точек пластины, можно построить поверхность текучести.
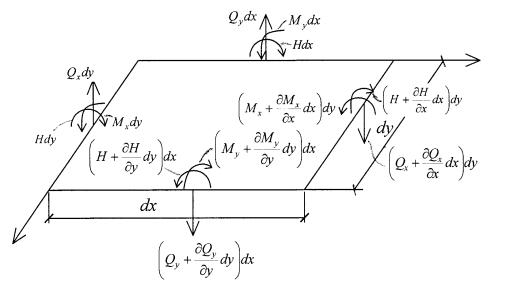
Как было ранее отмечено, М x0 , М y0, H 0 зависят от вида диаграммы
i i . Рассмотрим (рис. 5.2) диаграмму деформирования материала с площадкой текучести (диаграмма Прандтля).
Площадка текучести
Рис. 5.2
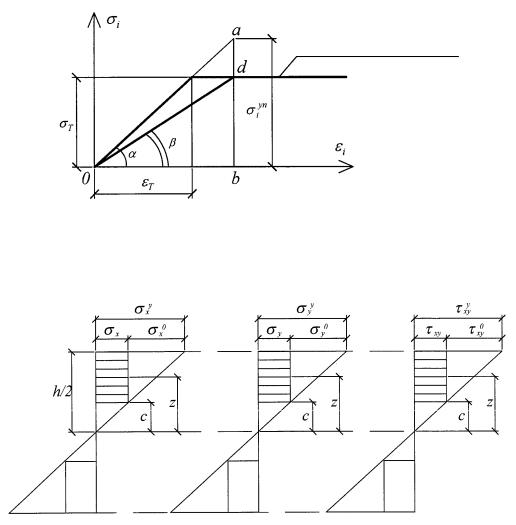
Распределение нормальных и касательных напряжений по толщине сечения приведено на рис. 5.3.
Рис. 5.3
Определим выражения моментов
110
