1697

Интегрируя по частям, используем функцию Грина [4]:

3w 4w

x2 y wcosnydS x2 y2 wdxdy;

y2w2 2xw2 dxdy y2w2 wx cosnxdS

3w 4w

y2 x wcosnxdS y2 x2 wdxdy;

2xw2 2xw2 dxdy 2xw2 wx cosnxdS

41

x2wy x2wy dxdy x2wy y wx dxdy

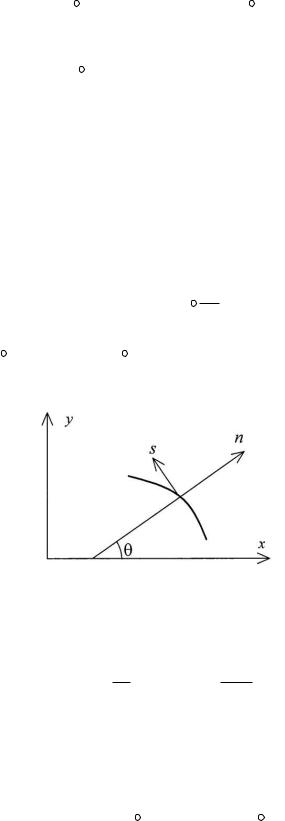
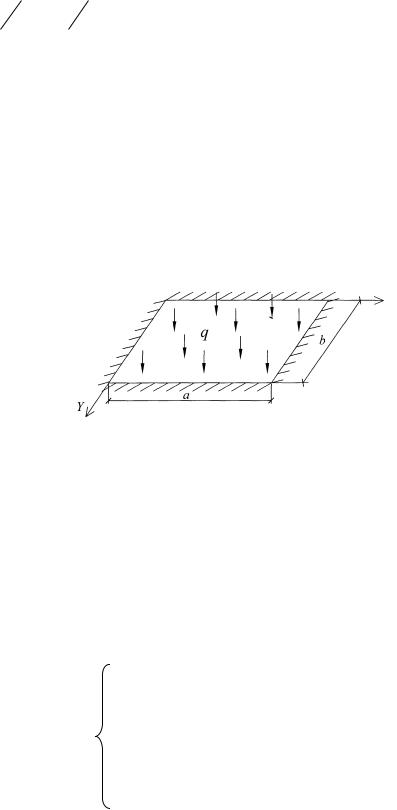
где n – внешняя нормаль к контуру пластины (рис. 3.4). Из рис. 3.4 следует, что

С учетом (3.22) выражение (3.19) принимает вид

42

U D 4w wdxdy D 2w wds

n

Рис. 3.4

Для замкнутого контура с учетом однозначности функции Ht имеем

Ht w ds Ht wds.

s s

(3.25)

Внося (3.25) в (3.24), получаем

43

где Qt – поперечная сила на контуре пластины,

Qt D 2w.s

(3.27)

Выражение (3.26) впервые получено Г.Р. Кирхгоффом [5]. С учетом (3.26) уравнение Лагранжа (3.18) принимает вид

(3.28)

Из полученного уравнения можно получить уравнение равновесия пластины С. Жермен-Лагранжа, а также условия для функции прогибов w(x,y). Поскольку w внутри контура пластины произвольна, то из (3.28)

следует известное уравнение изгиба пластины D 4w q.

Кроме того, поскольку на контуре пластины выполняются условия

w

w 0; 0, то граничное условие

n

(3.29)

выполняется соответствующим выбором искомой функции w(x,y). Тогда в выражении (3.28) остается одно слагаемое

D 4w q wdxdy 0.

(3.30)

Полученное уравнение (3.30) называется вариационным уравнением Б.Г. Галеркина.

При решении задачи об изгибе прямоугольной пластины вариационными методами функцию вертикальных перемещений w задают выражением, представляющим собой ряд

w Cm wm x, y .

m

(3.31)

44

При этом функции wm x, y выбирают так, чтобы они удовлетворяли геометрическим граничным условиям на контуре пластины wm 0;

wm 0.n

Для вариации w получаем w wm Cm.

m

Внося (3.31) и геометрические условия в (3.30), получим для определения неизвестных постоянных Cm столько линейных уравнений, сколько имеется постоянных.

На опертом контуре пластины wm 0.

Вследствие этого из (3.29) следует граничное условие на опертой части контураHt 0.

Это есть статическое граничное условие, получаемое из вариационного уравнения. При решении это условие можно заранее не удовлетворять.

На свободной части контура вариация w отлична от нуля, поэтому из граничного условия (3.29) следуют граничные условия на свободной

части контура пластины Ht 0; Qt Ht 0.

s

Эти статические условия на свободной части контура получаются как следствие вариационного уравнения. Ранее эти условия были получены в виде (2.22) Mx x a 0; H x a 0; Qx x a 0.

При приближенном решении, когда исходят из вариационного уравнения (3.18), не надо заранее удовлетворять статические граничные условия, т.к. они выполняются автоматически. Геометрические граничные условия следует удовлетворять обязательно.

При решении вариационного уравнения, когда удовлетворяются геометрические и статические граничные условия, остается уравнение

(3.30).

При приближенном решении изгиба пластин, основанном на вариационном уравнении Лагранжа, ограничивается свобода деформаций пластин, т.е. на нее налагаются связи. Пластина становится жесткой, и деформации по величине становятся меньше. Значения прогибов, получаемые вариационным методом, получаются меньше прогибов, получаемых при точном решении, когда удовлетворяются дифференциальное уравнение равновесия и все граничные условия.

3.4. Метод Ритца

Вариационный метод, предложенный швейцарским физиком В. Ритцем [4] в 1908 г., состоит в том, чтобы от континуальной формулировки задачи

45

перейти к дискретной, когда функционал Э(w) заменяется

функциейЭ(Сij ), зависящей от конечного числа аргументов Сij .

Задача определения экстремума функционала переходит в задачу исследования функции дискретного числа аргументов на экстремум. Задача с бесконечным числом степеней свободы в отношении формы деформирования пластины переходит в задачу для системы с конечным числом степеней свободы.

Рассмотрим применение метода Ритца к решению задачи изгиба пластин.

Полную энергию пластины определяем по известному уравнению

Э U П.

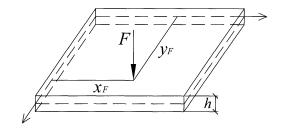
Пусть прямоугольная пластина со сторонами а, b и толщиной h оперта по контуру, нагружена равномерно распределенной нагрузкой q и сосредоточенной силой F, приложенной в точке K с координатами xF , yF

(рис. 3.5).

x

К

y

Рис. 3.5

Полная энергия пластины, согласно вышеизложенному, будет равна

ab

qwdxdy Fw xF ,yF .

00

(3.32)

Если кромки пластины остаются прямолинейными при ее деформировании, то выражение (3.32) принимает вид

(3.33)

46

Коэффициенты Kij и aij из решения системы получаются

где fi – вторая производная по x; j – вторая производная по y.

Вычислив интегралы и коэффициенты Cij , находим функцию

прогибов w(x,y).

Внутренние усилия в пластине находим по известным зависимостям, подставляя в них найденное выражение w(x,y).

Mx DCij fi j fi j ;

M j DCij fi j fi j ;

H D 1 Cij fi j ;

(3.40)

Qx DCij fi ' j j fi ;

Qy D Cij fi j fi j ' .

Напряжения по толщине пластины находим по формулам

(3.41)

где z – расстояние от нейтральной плоскости пластины до точки, где определяем напряжения.

Рассмотрим ряд случаев опирания граней пластины.

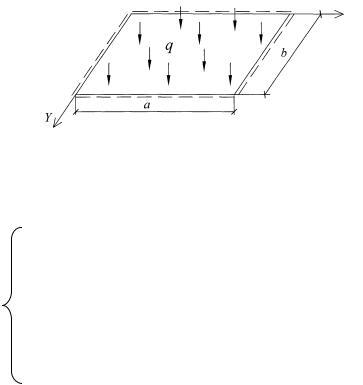
1. Все четыре грани имеют шарнирное опирание (рис. 3.6).

48

x

y

Рис. 3.6

В этом случае функцию прогибов, удерживая m и n членов разложения, задаем в виде

Значение коэффициента Cij получаем в виде

(3.43)

Выражение для функции прогиба w

Полученная формула совпадает с методом Фурье; если ограничиться одним членом ряда (m 1; n 1), то для wmax получаем

49

Максимальные изгибные напряжения имеют место в центре пластины

Касательные напряжения от крутящего момента в центре пластины равны нулю.

2. Кромки пластины защемлены (рис. 3.7).

x

y

Рис. 3.7

В этом случае функцию прогибов, удерживая в разложении функции один член ряда, задаем в виде

w Cij x a 2 x2 y b2 y2.

(3.47)

Функция прогибов w удовлетворяет геометрическим граничным условиям

50