1697

Так как последнее уравнение должно выполняться для всех значений x и y, то

Коэффициенты amn определяются по (2.45).

Полученное выражение для функции прогибов (2.48) является решением задачи об изгибе прямоугольной пластины, находящейся под действием поперечной нагрузки q(x,y).

Формулы для определения усилий в пластине можно получить, используя выражения, полученные в разделе 1.

Рассмотрим частные случаи загружения пластины.

1. Нагрузка равномерно распределена по всей поверхности пластины.

В этом случае q(x,y) = q = const. Из формулы (2.45) находим

где m и n – нечетные числа. Все коэффициенты amn при четных m и n равны нулю.

Функция прогибов принимает вид

31

При равномерно распределенной нагрузке изогнутая поверхность пластины должна быть симметричной. Если оси координат выбраны, как указано на рис. 2.4, то члены с четными m и n отвечают несимметричным прогибам и поэтому равны нулю. Наибольший прогиб пластины имеет место в центре:

Этот ряд сходится достаточно быстро, и первые несколько членов дают удовлетворительный результат.

В случае квадратной пластинки (a = b), принимая = 0.3, определим прогиб первыми четырьмя членами ряда:

w x a/2;y b/2 0,0443q0Eha3 4 ,

где Е – модуль упругости материала пластины; h – толщина пластины.

По известной функции прогибов можно найти изгибающие моменты в пластине:

Наибольший момент будет в центре пластины. Для квадратной пластины (a = b)

32

Изгибные напряжения в пластине:

Наибольшие напряжения при изгибе имеют место при z h

2

qa2

max 0,287 h2 .

min

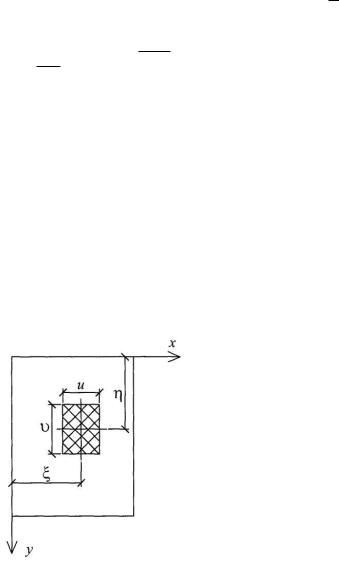
2. Нагрузка равномерно распределена по площади прямоугольника размерами u, (рис. 2.5). Используя выражение (2.45), получаем

Рис. 2.5

Функцию прогибов w(x,y) определяем по (2.48), и находим внутренние усилия Mx , M y , Н, Qx , Qy в пластине, а также напряжения

x , y , xy , xz , yz .

3.Нагрузка в виде сосредоточенной силы.

33

Пусть пластина загружена сосредоточенной силой в точке с координатами x ; y . Полагая, что u 0; 0, находим, используя выражение (2.53),

Вычислим прогиб в середине пластины, где приложена сила F. В этом случае x a /2; y b/2.

Зная функцию прогибов, можно найти изгибающие и крутящие моменты, поперечные силы. Ряды, входящие в выражения внутренних усилий, плохо сходятся, поэтому полученные результаты наиболее точно определяют только прогибы пластин. Для определения изгибающих моментов, поперечных сил, а тем более для напряжений применять рассмотренный метод нерационально.

34

3. ВАРИАЦИОННЫЕ МЕТОДЫ РАСЧЕТА ПРЯМОУГОЛЬНЫХ ПЛАСТИН

3.1. Основные понятия вариационного исчисления

Представленные в предыдущих разделах уравнения, описывающие напряженно-деформированное состояние в пластинах вместе с граничными условиями, трудно решить в аналитической форме, а численное решение сопряжено с громоздкими выкладками.

Для решения задач изгиба пластин весьма эффективны вариационные методы, математический аппарат которых разработан в разделе математики "Вариационное исчисление".

Состояние равновесия пластин наряду с дифференциальными уравнениями может быть описано с помощью вариационных принципов, разработанных в механике деформируемого твердого тела на основании вариационных методов [4].

Положение равновесия консервативной системы есть положение, в котором силовая функция системы имеет минимальное значение. Консервативной называется такая система, первоначальное положение внешних нагрузок в которой не изменяется в процессе деформирования системы

(рис. 3.1).

Рис. 3.1

Изложенное свойство упругих механических систем, к которым относится пластина, позволяет отказаться от прямого решения дифференциального уравнения и перейти к проблеме определения функции, обеспечивающей минимум некоторого функционала в теории пластин, носящего название полной энергии.

В инженерной практике наряду с задачами, в которых отыскивается экстремум некоторой функции y f x , имеют место такие, в которых необходимо отыскать экстремум некоторой переменной Ф, которая сама зависит от выбора функции y x . Такие переменные Ф называются

функционалами.

35

В простейшем случае функционал Ф представляется в виде интеграла

a

где a, b определяют интервал изменения аргумента х.

Сравнивая функционал и функцию, замечаем, что они являются переменными, однако первый зависит от вида функции y x , а вторая – от величины аргумента х.

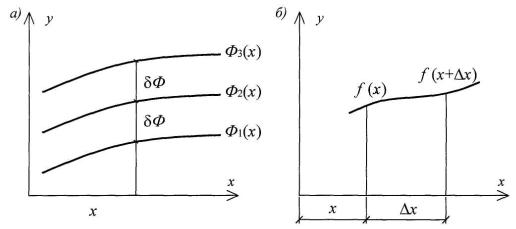
В первом случае, изменяя вид функции y x , т.е. варьируя функцию, изменяем величину функционала (рис. 3.2, а), а во втором, изменяя величину переменного х, определяем величину функции (рис. 3.2, б).

Рис. 3.2

Операция варьирования предполагает, что при фиксированном х имеет место переход от одной функции к другой. Операция дифференцирования предполагает неизменность вида функции на участке

x.

Методы решения вариационных задач, т.е. описания функций, сообщающих функционалу максимум или минимум, сходны с исследованием функции на максимум и минимум. В задачах на максимум или минимум независимому переменному х дается приращениеx х х1, равное дифференциалу x. В вариационных задачах дается приращение (вариация) для искомой функции y x , равное

36

В вариационном исчислении вариация функционала Ф представляет линейную по отношению к вариации функции y часть функционала.

Если функция y f x достигает экстремума внутри интервала, то dy 0; y' x 0.

Если функционал достигает экстремума, то его вариация равна нулю:

Вариационные методы, применяемые к расчету пластин, основаны на свойствах полной энергии при изгибе пластин.

3.2. Полная энергия деформации при изгибе пластин

через w(x,y) и интегрируя по z от h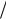2 до h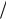2, получаем

37

где А – площадь срединной поверхности пластины; D – цилиндрическая жесткость пластины.

Проинтегрируем по частям второе выражение в квадратных скобках полученной формулы:

Потенциальная энергия изгиба пластины принимает вид

38

Dab 2w 2w

2

U 2 00 x2 y2 dxdy 0.

(3.11)

Полная энергия пластины представляет сумму потенциальной энергии U и потенциала внешних сил П:

Э U П.

(3.12)

Для пластин, загруженных только нагрузкой q(x,y), величина П определяется как работа элементарных сил qdxdy на перемещениях w при переходе изогнутой пластины в недеформированное состояние:

ab

П q x,y w x,y dxdy.

00

(3.13)

Если к пластине приложены еще какие-либо нагрузки, то в выражении для П должна быть добавлена работа этих нагрузок. Так, для пластины, показанной на рис. 3.3,

(3.14)

Рис. 3.3

В (3.14) учтена работа сосредоточенной силы F и моментов m, распределенных по грани с координатой х = 0.

3.3. Вариационное уравнение изгиба пластины

39

Рассмотрим выражение потенциальной энергии изгиба пластины:

Пусть пластина загружена поперечной нагрузкой q на единицу площади. Потенциал от действия нагрузки q имеет вид

П qwdxdy.

А

(3.16)

Полная энергия, как это было рассмотрено ранее, представляет собой сумму потенциала внешних и потенциальной нагрузок энергии пластины:

Э U П.

(3.17)

Вариационное уравнение Лагранжа [4] в этом случае примет вид

Э 0; U П 0.

(3.18)

Геометрические граничные условия для вертикальных линейных перемещений w могут быть:

1)если пластина оперта по всем граням, то w = 0;

2)если пластина заделана (защемлена) по всему контуру, то

добавляется еще одно геометрическое условие – w 0, где производная

n

взята по внешней нормали к контуру пластины, а n есть элемент нормали к контуру.

Таким образом, на вариации w налагаются условия:

w

1) w 0 на контуре; 2) 0 на контуре.

n

Из выражения для U (3.15) имеем

40