1697

Для сведения двумерной задачи об изгибе пластин функция прогибов w(x,y) представляется в виде суммы произведений функций, одна из которых известна, а функция другого направления определяется из решения дифференциального уравнения.

Уравнения равновесия для пластин В.З. Власовым получены из вариационного уравнения Лагранжа.

В отличие от метода Бубнова-Галеркина, где интегрирование дифференциального уравнения сводится к решению системы линейных алгебраических уравнений, в методе Канторовича-Власова интегрирование дифференциального уравнения в частных производных заменяется решением системы обыкновенных дифференциальных уравнений.

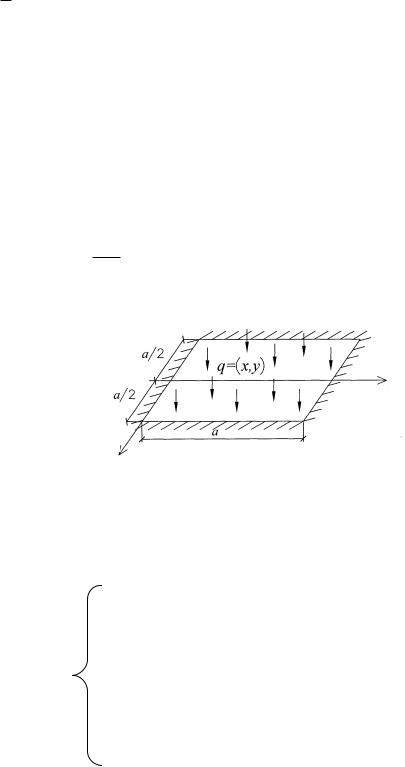
Рассмотрим пластину, две грани которой имеют шарнирное (рис. 3.11), а две другие – произвольное опирания:

x

y

Рис. 3.11

Представим прогиб пластины в виде

w Уm y fm x ,

m 1

(3.79)

где Уm y – функция, которую необходимо найти. В качестве функции направления x выбираем

fm x sin m x . a

(3.80)

Выбранная функция удовлетворяет граничным условиям на гранях x 0 и x a.

61

Функция прогибов в этом случае принимает вид

(3.81)

Распределенную нагрузку q x, y представим в виде ряда

(3.82)

Составим уравнение Бубнова-Галеркина при заданных w и q:

После интегрирования получим

62

Решая данное обыкновенное дифференциальное уравнение, находим функцию Уm y при заданных граничных условиях на гранях пластины

y b. 2

Определив функцию Уm y , можно определить функцию прогибов w x,y , а тем самым – внутренние усилия и напряжения в пластине.

В качестве примера рассмотрим квадратную защепленную по контуру, загруженную равномерно распределенной нагрузкой q пластину

(рис. 3.12).

Зададим функцию прогибов w в виде

w У y f x ,

(3.87)

где f x 1 cos 2 x . a

x

y

Рис. 3.12

Функция f x удовлетворяет геометрическим граничным условиям опирания пластины на гранях (x 0;x a).

63

Подставляя функцию прогибов в уравнение Бубнова-Галеркина, получаем

(3.89)

Производя интегрирования, получаем линейное дифференциальное уравнение четвертого порядка с постоянными коэффициентами

Общее решение уравнения (3.90) отыскиваем в виде суммы общего решения однородного дифференциального уравнения и частного решения неоднородного дифференциального уравнения, зависящего от вида правой части:

64

Максимальный прогиб в центре пластины (x a2; y 0) равен

wmax 0,00129 qa4 .

D

Найденное значение максимального прогиба с точностью до 1 % совпало с решениями, полученными методами Ритца и Бубнова-Галеркина.

3.7. Метод конечных элементов

Одним из вариантов вариационных методов, применяемых при расчетах пластин, является метод конечных элементов (МКЭ). Рассмотрим

65

прямоугольную пластину под действием произвольной поперечной нагрузки q (рис. 3.13).

Разобьем пластину на прямоугольные элементы со сторонами a и b.

x

y

z

Рис. 3.13

В каждом узле задаем по три перемещения: одно линейное w и два

угловых ( w и w).

x y

Прогибы и углы поворота в узловых точках для прилегающих к узлу конечных элементов равны между собой.

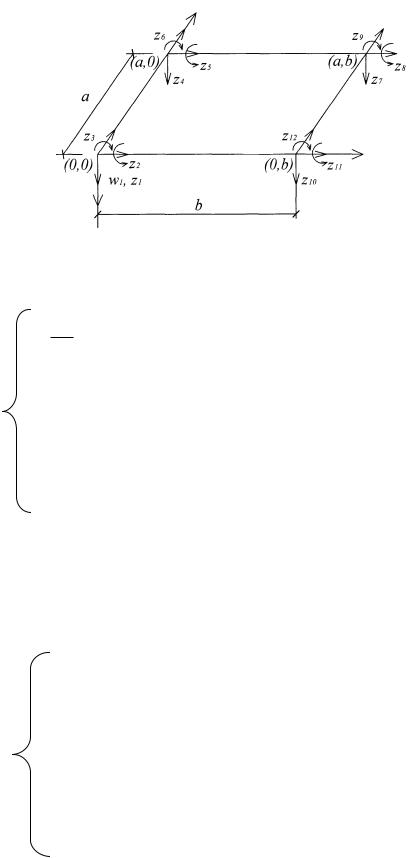
Перемещение в узлах конечного элемента обозначим через z1, z2 , …, z12 (рис. 3.14).

Прямоугольный конечный элемент ABCD (см. рис. 3.13) имеет двенадцать степеней свободы перемещений.

В соответствии с этим функцию перемещений между узловыми точками зададим полиномом двенадцатой степени:

w x, y 1 2x 3 y 4x2 5xy 6 y2 7x3

66

x

y

z, w

Рис. 3.14

Углы поворота i-го узла:

wy i 3 5xi 2 6 yi 8xi2 2 9 xi yi

3 10 yi2 11xi3 3 12 xi yi2;

(3.98)

9 yi2 3 11xi2 yi 12 yi2.

На рис. 3.14 показаны положительные направления векторов перемещения узловых точек z1, …, z12 .

Для узловых перемещений можно получить выражения

67

Функцию w x, y можно представить в виде полиномов Эрмита [8]

wa11Э01 x Э01 y a12Э01 x Э02 y a21Э02 x Э01 y

a22Э02 x Э02 y b11Э11 x Э01 y b12Э11 x Э02 y

b21Э21 x Э01 y b22Э12 x Э02 y c11Э01 x Э11 y

c12Э01 x Э12 y c21Э02 x Э11 y c22Э02 x Э12 y .

(3.100)

Полиномы Эрмита имеют вид

68

Функцию прогибов представим через перемещения zi :

wz1Э01 x Э01 y z2Э11 x Э01 y z3Э01 x Э11 y

z4Э02 x Э01 y z5Э12 x Э01 y z6Э02 x Э11 y

z7Э02 x Э02 y z8Э12 x Э02 y z9Э02 x Э12 y

Э02 x Э02 y z8Э12 x Э02 y z9Э02 x Э12 y .

(3.103)

Вводим функции i x,y :

Функцию прогибов выразим через i x, y , тогда узловые перемещения будет определять выражение

12

wzi i x, y .

i1

(3.105)

Выражение (3.105) обеспечивает условие непрерывности w, w, w

x y

между узлами по линии контакта элементов.

Выразим узловые усилия Ri через узловые перемещения, используя принцип возможных перемещений.

Уравнение Лагранжа для равновесия пластины через выражение перемещения zi для отдельного элемента имеет вид

Ri zi U .

(3.106)

Выражение потенциальной энергии конечного элемента пластины при его изгибе берем в виде

(3.107)

69

Используя (3.105), находим

12

2w zi 2 i ; i 1