Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1697

.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

1.58 Mб

Скачать

☆

<<< < Предыдущая 12 / 132 3 4 5 6 7 8 9 10 11 12 13 > Следующая >>>

Подставляя в (1.12) выражение (1.10), получаем

E z

;

E z

;

E z

хy

1 x y

(1.13)

где – коэффициент Пуассона.

Формулы (1.13) показывают, что напряжения x , y , xy в точках

срединной поверхности равны нулю.

По закону Гука, используя вторую гипотезу, имеем

		E		0;
	хz		xz

		21
		21
		E
		E		0.

	yz	21	yz
	yz		yz
				(1.14)
				(1.14)
В действительности хz	и	yz не	равны нулю. Рассмотрим

дифференциальные уравнения равновесия Навье при отсутствии объемных сил [1]:

хy

хz

zх

(1.15)

Из первого уравнения в (1.15) находим

õz

õy

E z

x y

(1.16)

После приведения подобных получаем

хz

E z

(1.17)

где

– дифференциальный оператор Лапласа.

Интегрируя (1.17) по z, получаем

хz zx

E z2

2w f3

x, y .

21 2 x

(1.18)

Используя граничные условия хz

при z

, находим

f3 x, y

E h2

2w.

81 2 x

(1.19)

Получаем выражение для zx :

2w.

хz

(1.20)

Решая второе уравнение в (1.15), получаем

2w.

(1.21)

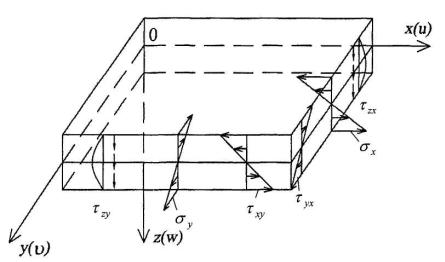
Покажем распределение напряжений на двух взаимноперпендикулярных кромках (рис. 1.3). Часть напряжений имеет тот же смысл, что и в балках, с той лишь разницей, что в пластинах изгиб происходит в двух направлениях. Это относится к напряжениям x и zx для направления ox и напряжениям y , zy в направлении oy. Пластина,

кроме изгиба в двух направлениях, испытывает кручение, в результате чего возникают касательные напряжения xy и yx .

Рис. 1.3

1.4. Определение внутренних усилий и напряжений

При расчете пластин в основном используют выражения для определения усилий. Внешними нагрузками, действующими на пластину, как правило, являются усилия, распределенные на единицу длины. В пластинах напряжения и усилия являются переменными по высоте сечения.

Вырежем из пластины бесконечно малый элемент размерами dx и dy (рис. 1.4), который находится в равновесии при действии на него усилий:

изгибающего	момента	M x ,	создаваемого	действием
равнодействующей напряжений x ;
изгибающего	момента	M y,	создаваемого	действием
равнодействующей напряжений y ;

крутящего момента Н, создаваемого действием равнодействующей касательных напряжений xy и yx ;

продольной силы Nx, действующей в направлении оси ox;

поперечной силы Qx , действующей в сечении с нормалью, совпадающей с осью ox;

поперечной силы Qy , действующей в сечении с нормалью,

совпадающей с осью oy.

Рис. 1.4

Определим усилия, приходящиеся на единицу высоты:

h/2

xdz

zdz;

h/2

(1.22)

2w z2 h/2

2 h/2

(1.23)

Выражение (1.23) показывает, что нормальной силы в сечении с нормалью, совпадающей с осью ox, не возникает. Аналогично Ny 0.

Далее запишем выражение для определения изгибающего момента

Mx:

h/2

2w h/2

M x

x zdz

dz;

h/2

(1.24)

z3 h/2

M x

;

3 h/2

(1.25)

M x

2 .

(1.26)

Обозначим

Eh3

121 2 .

(1.27)

Параметр D носит название цилиндрической жесткости пластины и

является физической и геометрической характеристикой пластины при изгибе.

С учетом (1.27) получаем

M x D

(1.28)

Аналогично определяем M y :

h/2

M y

y zdz D

h/2

(1.29)

Определим погонную поперечную силу в сечении с нормалью, совпадающей с осью ox:

h/2

Qx zxdz.

h/2

(1.30)

С учетом выражения zx из (1.20) получаем

	E		h2			2		2	h/2	h2

Qх		2			z				w
				4			x				4
	21								h/2

После вычислений в (1.31) находим

Qх D 2w.x

Аналогично определяем Qy :

	h/2		2w.
Qy	yzdz D

	h/2	y

z2 dz.

(1.31)

(1.32)

(1.33)

Определим сдвигающую силу в сечении с нормалью, совпадающей с осью ox:

h/2

w z

2 h/2

yxdz

zdz

1 x y

1 x y 2

h/2

(1.34)

Таким образом, сдвигающая сила в этом сечении равна нулю. Аналогично

	h/2
Sy	xydz 0.
	h/2

(1.35)

Определим крутящий момент в сечении с нормалью, совпадающей с осью ox:

h/2

z2dz

w z

3 h/2

yxzdz

;

1 x y

1 x y 3

h/2

(1.36)

h/2

D 1

yx zdz

h/2

1 12 x y

x y

(1.37)

Полученные выражения показывают, что найденные внутренние усилия, возникающие в поперечных сечениях пластины, являются функциями прогиба w и ее производных.

Подставляя выражения M x , M y , Qx , Qy , Н в (1.13), (1.20), (1.21),

получим формулы для определения напряжений, выраженные через внутренние усилия:

12Mx

12M y z

12H z

; y

; xy yx

;

6Qx

;

(1.38)

2. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ИЗОГНУТОЙ ПОВЕРХНОСТИ ПЛАСТИНЫ

2.1. Уравнения равновесия элемента пластины

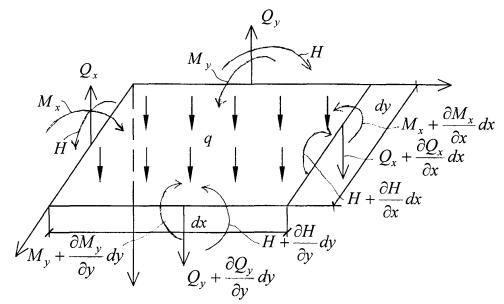
Рассмотрим бесконечно малый элемент срединной плоскости пластины, находящейся под действием внешней, распределенной на единицу площади, нагрузки q (рис. 2.1). В общем случае q может быть переменной, но для бесконечно малого элемента примем ее постоянной.

По граням элемента x=0; y=0 будут действовать изгибающие моменты M x и M y , крутящие моменты Н, а также поперечные силы Qx и Qy . Так

как внутренние усилия являются функциями координат x, y, то на противоположных гранях с координатами x dx и y dy усилия получат соответствующие приращения.

Разлагая эти усилия в ряды Тейлора [2] с точностью до малых первого порядка, получаем

M y

Mx x dx Mx

dx;

M y y dy M y

dy;

x dx H

dx; H y

dy H

dy;

(2.1)

x dx Q

y dy Q

dx;

dy.

Рис. 2.1

Кроме изгибающих и крутящих моментов по граням элемента будут действовать вертикальные поперечные силы, соответствующие

касательным напряжениям zx	и yz.	Поперечные			силы для этих
напряжений:
	h/2			h/2
Qx	zxdz;	Qy		yzdz.
h/2				h/2		(2.2)
						(2.2)
Согласно принятым гипотезам zx		zx	0; yz		yz	0.
		zx
					G
		G			G

Но при составлении уравнений равновесия в них необходимо включить результирующие силы, соответствующие касательным напряжениям zx и zy .

Интенсивность нагрузки q равна напряжению z на верхней поверхности пластины, т.е. z является величиной порядка q. Согласно принятым гипотезам величина z пренебрежимо мала, т.е. равна нулю.

Принимаем в выражениях

Слагаемые

малы по сравнению с другими слагаемыми,

G G

считаем поперечные силы Qx и Qy величинами того же порядка, что интенсивность нагрузки q и моменты M x , M y , Н.

Составим уравнения равновесия для выделенного элемента:

z Qx dxdy Qy dydx qdxdy 0.

x y

(2.3)

После сокращения имеем

Qx Qy q 0.x y

(2.4)

M y

dx dy Hdy

M y

dx M ydx H

dxdy

dy dxdy Q

dx dy

qdxdy

(2.5)

dx dy M

dy dx

Hdx

dxdx

(2.6)

dx dxdy Qy

qdxdy

Пренебрегая бесконечно малыми третьего порядка, после упрощения получаем

Mx H Qx;x y

(2.7)

H M y Qy.x y

(2.8)

Уравнения (2.4), (2.7) и (2.8) называются уравнениями равновесия элемента пластины.

В эти три статических уравнения входят пять неизвестных функций M x , M y , Н, Qx , Qy . Поэтому задача определения внутренних усилий в

сечениях пластины является статически неопределимой. Эту задачу можно решить, если одновременно определить функцию прогибов w(x,y).

2.2. Основные дифференциальные уравнения изгиба пластины

Подставляя в (2.4) найденные значения поперечных сил, получаем

2Mx	2	2H	2M y	q.

x2			y2
		x y

(2.9)

Учитывая выражения моментов (1.28), (1.29) и (1.37),

<<< < Предыдущая 12 / 132 3 4 5 6 7 8 9 10 11 12 13 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.20211.57 Mб61692.pdf
#
07.01.20211.57 Mб41693.pdf
#
07.01.20211.58 Mб71694.pdf
#
07.01.20211.58 Mб01695.pdf
#
07.01.20211.58 Mб121696.pdf
#
07.01.20211.58 Mб121697.pdf
#
07.01.20211.58 Mб101698.pdf
#
07.01.20211.59 Mб31699.pdf
#
07.01.2021201.28 Кб517.pdf
#
07.01.2021324.32 Кб0170.pdf
#
07.01.20211.59 Mб91700.pdf