
1697
.pdf
при y 0; |
y b |
|
|
w 0; |
||||
|
w |
|
y 0 |
0 |
; |
w |
|
y b 0. |
|
|
|
||||||
|
y |
|
y |
|
||||
|
|
|
|
|
|
|
||
Для коэффициента Cij после вычислений получаем
C |
|
qa4 |
|
|
1 |
|
|
|
. |
||
4D 4 |
a 4 |
a 2 |
|||||||||
11 |
|
|
|
||||||||
|
|
|
|
3 3 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
b |
b |
|
|||||
(3.49)
Для квадратной пластины (a b; 0,3)
w 0,0140 qa4 . |
|
max |
Eh3 |
|
|
(3.50)
Если прямоугольная пластина загружена сосредоточенной силой F , расположенной в центре, то наибольший прогиб будет
w 0,0593 Fa2 . |
|
max |
Eh3 |
|
|
(3.51)
3.Две грани защемлены, а две другие шарнирно оперты.
Рассмотрим прямоугольную пластину, края которой x 0; x a
защемлены, а два края y 0; y b шарнирно оперты (рис. 3.8). Функцию прогибов в первом приближении задаем в виде
|
|
|
|
w C |
x2 x a 2 sin |
y |
. |
|||
|
|
|
|
|
||||||
|
|
|
|
11 |
|
|
b |
|||
|
|
(3.52) |
|
|
||||||
|
|
|
|
|
|
|||||
Геометрические граничные условия на кромках при x 0; |
x a: |
|||||||||
|
w |
|
|
y |
|
|
|
|
||
|
|
|
|
|
|
|
||||
w 0; |
|
|
x 0,x a С11sin |
|
2x x a 2 2x2 x a 0. |
|||||
x |
b |
|||||||||
|
|
|||||||||
|
|
|
|
|
|
|
(3.53) |
|||
51
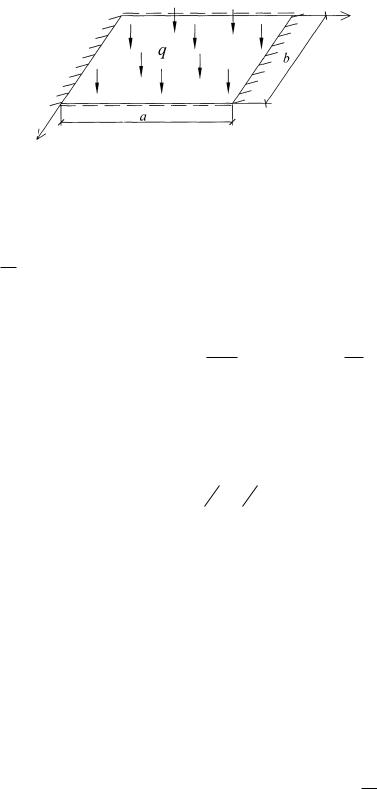
x
y
Рис. 3.8
Как видно, геометрические граничные условия на кромках пластины выполняются.
После интегрирования находим значение коэффициента
C11 0,3072 q .
D
Функция прогибов имеет вид
w 0,3072 qa4 x2 x a 2 sin y .
D b
(3.54)
Прогиб в центре пластины
w |
w |
|
x a |
2,x b |
|
0,0192 |
qa4 |
. |
|
|
|||||||
|
|
|
||||||
max |
|
|
2 |
|
D |
|||
(3.55)
Полученное значение wmax совпадает с решением по методу Фурье. Зная выражение функции прогибов во всех приведенных случаях, можно найти M x , M y , H , Qx , Qy в любой точке пластины, а также
напряжения x , y , xy.
3.5. Метод Бубнова-Галеркина
Как было ранее отмечено, из вариационного уравнения Лагранжа при выполнении геометрических и статических граничных условий следует уравнение
4w q 0.
D
(3.56)
По методу Б.Г. Галеркина [6] функцию перемещений w x, y задаем в виде
52

m n
wmn Cij fi x j y , i 1 j 1
|
(3.57) |
где Cij – коэффициенты, подлежащие определению; fi x , |
j y – |
функции, удовлетворяющие геометрическим и статическим условиям на гранях пластины.
Подставляя w x, y в уравнение (3.56), получаем функцию - "невязку", отличную от нуля:
4wmn q Ф xy 0.
D
Требуя, чтобы работа "невязки" на возможных перемещениях fi x ,j y по всей площади пластины равнялась нулю, получаем систему линейных алгебраических уравнений для определения коэффициентов Cij .
a b |
4w |
|
|
|
q |
|
x |
|
y dxdy 0. |
|
||
|
|
mn |
|
|
|
f |
i |
j |
|
|||
|
|
|
||||||||||
|
|
|
|
D |
|
|
|
|||||
0 0 |
|
|
|
|
|
|
|
|
(3.58) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
Число линейных уравнений равно m n. |
|
|
|
функций fi x , |
j y |
|||||||
При удачном выборе аппроксимирующих |
|
|||||||||||
можно ограничиться одним членом ряда
w Cij fi x j y .
(3.59)
Подставляя (3.59) в (3.58), получаем одно уравнение для определения параметра Cij :
a b |
4w |
4w |
|
|
4w |
q |
|
x j y dxdy 0. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
4 2 |
x |
2 |
x |
2 |
y |
4 |
D |
fi |
||||
0 0 |
|
|
|
|
|
|
|
|
|
|||||
После упрощений имеем
53

|
|
|
q a |
b |
|
|
|
|
|
|
fi x dx j y dy |
|
|
|
|
|
D |
|
||
Cij |
|
|
|
0 |
0 |
|
a |
b |
a |
b |
y j y dy |
||
|
fi IV x fi x dx j2 y dy 2 fi x fi x dx j |
|||||
0 |
0 |
|
0 |
0 |
|
|
,
a b
fi2 x dx j y IVj y dy
|
0 |
|
0 |
(3.60) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x |
d2 fi |
IV |
x |
d |
4 fi |
|
|
y |
d2 j |
|
IV |
y |
d4 j |
|
где fi |
|
; fi |
|
|
; |
j |
|
; j |
|
|
. |
||||
dx2 |
dx4 |
dy2 |
|
dy4 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
После определения Cij |
находим |
функцию прогибов w x, y . Тем |
|||||||||||||
самым можем найти внутренние усилия и напряжения в любой точке пластины.
Рассмотрим несколько примеров расчета пластины методом Бубнова-Галеркина.
1. Пластина, шарнирно опертая по всем граням, нагружена равномерно распределенной нагрузкой q (рис. 3.9).
x
q=const
y
Рис. 3.9
Граничные условия опирания:
x 0: |
w 0; |
Mx |
|
|
|
|
2w |
|||
0 |
; |
|
|
|
|
|
0; |
|||
|
|
|
||||||||
|
|
|
|
|
|
|
x2 |
|||
|
w 0; |
Mx |
|
|
2w |
|||||
x a: |
0; |
|
|
|
|
0; |
||||
|
|
|
|
|||||||
|
|
|
|
|
x2 |
|||||
|
|
|
|
|
|
|
|
(3.61) |
||
y 0: |
w 0; |
My |
0 |
|
|
|
2w |
|||
; |
|
|
|
|
|
0; |
||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
y2 |
|||
54

y b: |
w 0; |
My |
0 |
|
|
2w |
|
; |
|
|
0. |
||||
|
|
||||||
|
|
|
|
|
y2 |
||
Функцию прогибов задаем в виде
wij Cij sin i x sin j y . a b
(3.62)
Найдем значения wij и ее вторых производных на гранях пластины:
|
x 0: |
|
|
wij Cij |
sin |
i 0 |
|
sin |
|
j y |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2wij |
|
|
|
i |
|
2 |
|
i x |
|
|
|
j y |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Cij |
|
|
|
|
sin |
|
|
sin |
|
|
|
; |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
a |
|
a |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2wij |
|
|
|
x 0 0; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
x a: |
|
|
wij Cij |
sin |
i a |
sin |
j y |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2wij |
i |
2 |
i a |
|
|
|
j y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.63) |
|||||||||||||||||||||||||||
|
Cij |
|
|
|
sin |
|
|
|
sin |
|
|
|
|
0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
x2 |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
a |
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
i x |
|
|
|
|
|
|
|
j 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
y 0: |
|
|
|
|
wij |
Cij |
sin |
sin |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2wij |
|
j |
2 |
|
|
i x |
|
j y |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
sin |
|
|
; |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 |
|
a |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
b |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2w |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ij |
|
y 0 0; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
y b: |
|
|
|
|
wij |
Cij |
sin |
x |
sin |
i b |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
2wij |
j |
2 |
|
i x |
|
|
|
i y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
Cij |
|
|
|
sin |
|
|
|
sin |
|
|
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
y2 |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
b |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Таким образом, функция w x, y ij удовлетворяет на гранях пластины
и геометрическим, и статическим граничным условиям. Вычисляя производные функций fi x и j y , получим
55
|
i 2 |
x |
IV |
i 4 |
|
x |
|||||||||||||
fi |
x |
|
|
sin |
|
|
; |
fi |
x |
|
|
sin |
|
|
; |
||||
|
|
|
|
|
|
||||||||||||||
|
|
a |
|
|
a |
|
|
a |
|
|
a |
||||||||
|
|
j 2 |
|
|
|
|
|
|
|
j 4 |
|
(3.64) |
|||||||
|
|
|
|
y |
IV |
|
|
y |
|||||||||||
j |
y |
|
|
|
sin |
|
; |
j |
y |
|
|
|
sin |
|
. |
||||
|
|
|
|
|
|
||||||||||||||
|
|
b |
|
|
b |
|
|
b |
|
|
b |
||||||||
После подстановки производных в (3.60) и интегрирования получаем
Cij |
|
|
|
16 qa4 |
|
|
|
sin |
i x |
sin |
j y |
. |
|||||
|
|
|
|
|
|
|
|
2 |
|
|
|
a |
b |
||||
|
|
6 |
|
|
2 |
|
a |
|
2 |
|
|
|
|||||
|
|
D |
|
i |
|
|
j |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
b |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(3.65)
Функция прогибов при удержании в ее разложении одного члена ряда примет вид
wij |
|
|
|
16 qa4 |
|
|
|
|
i x |
j y |
. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
sin |
|
||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
b |
||||
|
|
6 |
|
|
2 |
|
a |
|
2 |
|
a |
|
|||||
|
|
D |
|
i |
|
|
j |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
b |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(3.66)
Поскольку система линейных уравнений (3.58) распадается по отдельным гармоникам, то, удерживая в разложении (3.57) m членов ряда в направлении x и n членов ряда в направлении y , для функции прогибов получим
|
|
16 qa |
4 |
m n |
sin |
i x |
sin |
j y |
|
|||||||||
|
|
|
|
b |
|
|||||||||||||
wmn |
|
|
|
|
|
|
a |
|
|
|
|
|
. |
|||||
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
D i 1 j 1 |
|
2 |
|
a |
|
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
j |
|
ij |
||
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(3.67)
Функция прогибов, полученная по методу Галеркина, совпадает с выражениями w x, y , полученными по методу Фурье и методу Ритца.
Функция, которая в методе Бубнова-Галеркина удовлетворяет только геометрическим граничным условиям, не всегда приводит к точному решению.
Зададим функцию прогибов в виде
56

w C11x x a y b y,
(3.68)
где при вычислении С11 по формуле (3.60)
f1 x x a x; |
f1II x 2x a; |
f1IV x 0; |
||
1 y y b y; |
1II y 2y b; |
1IV y 0. |
||
Эта функция удовлетворяет на контуре пластины только геометрическим граничным условиям:
x 0: |
w 0 0 a y y b 0; |
|
|
|
|
|
M x |
2w |
2 0 a 0; |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2w |
|
|
|
x2 |
|
||||||||||||
x a: |
w a a a y y b 0; |
M |
x |
|
2 а a 0; |
(3.69) |
|||||||||||||||||||||||||
|
x |
2 |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
y 0: |
w x x a 0 0 b 0; M y |
|
|
2w |
|
x x a 2 0 b 0; |
|||||||||||||||||||||||||
y2 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
y b: |
w x x a b b b 0; |
M y |
|
2w |
|
|
x x a 2b b 0. |
|
|||||||||||||||||||||||
y2 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Определяем C11 по формуле (3.60): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
C11 |
|
|
|
qa2b2 |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
||||||||
|
|
|
a4 |
|
|
a2b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
b4 |
|
||||||||||||||||||||
|
|
|
|
24D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
5 |
|
|
|
|
3 |
|
|
|
|
|
|
5 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.70) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Прогиб пластины определяется |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
w x, y |
qa2b2xy x a y b |
. |
|
||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
a4 |
|
a2b2 |
|
|
|
|
|
b4 |
|
|||||||||||||||
|
|
|
|
|
24D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
5 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
(3.71) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Определим максимальный прогиб для центра квадратной пластины, |
|||||||||||||||||||||||||||||||
если b a; |
x a |
2; y b |
2: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
57 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
wmax 0,00356qa4 .
D
(3.72)
Полученный результат отличается от точного решения на 12,8 %. Очевидно, что выражение (3.68) не подходит для решения данной
задачи, т.к. не выполняются статические граничные условия.
2. Пластина, защемленная по контуру.
Рассмотрим пластину под действием равномерно распределенной нагрузки q, грани которой защемлены (рис. 3.10).
x
q=const
 y
y
Рис. 3.10
Приближенное выражение прогибов выражаем в виде ряда
|
m n |
|
|
2i x |
2j y |
|||||
|
wmn Cij 1 cos |
|
1 cos |
|
|
; |
||||
|
|
|
|
|||||||
|
i 1 j 1 |
|
|
a |
|
b |
||||
|
|
|
|
|
|
|
|
(3.73) |
||
fi |
x 1 cos |
2i x |
; |
j y 1 cos |
2 j y |
. |
||||
a |
|
|||||||||
|
|
|
|
|
|
b |
|
|
|
|
Граничные условия на кромках пластины:
|
|
|
|
|
|
m n |
|
|
|
|
2i 0 |
|
|
|
|
|
2j y |
|
|
|
||||||||
x 0: |
wmn Cij |
1 cos |
|
|
|
|
1 cos |
|
|
|
|
|
0; |
|||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
i 1 j 1 |
|
|
|
|
|
|
a |
|
|
|
|
b |
|
|
|
|||||||
|
|
|
|
|
|
|
|
m n |
|
|
|
|
|
|
2i a |
|
|
|
2j y |
|
||||||||
x a: |
|
wmn Cij 1 cos |
|
|
|
1 cos |
|
|
|
0; |
||||||||||||||||||
|
a |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
i 1 j 1 |
|
|
|
|
|
|
|
|
|
|
|
b |
|
|||||||
w |
mn |
|
|
2 |
m n |
|
|
i x |
|
|
|
|
2j y |
|
|
|
|
|
|
|
||||||||
|
|
|
|
Cij sin |
|
|
1 cos |
|
|
|
; |
|
|
|
|
|
|
|
||||||||||
x |
a |
|
|
b |
|
|
|
|
|
|
|
|
||||||||||||||||
|
i 1 j 1 |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
wmn |
|
|
|
2 |
m n |
|
|
|
|
i a |
|
2j y |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
x a |
|
|
Cij |
sin |
|
|
1 cos |
|
|
|
0; |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
x |
|
|
|
a |
i 1 j 1 |
|
|
|
|
a |
|
|
b |
|
|
|
|
|
|
|
||||||||
58
|
|
|
|
|
wmn |
|
|
|
|
|
|
|
2 |
m n |
|
|
|
|
|
|
i 0 |
|
|
|
|
2j y |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
Cij |
sin |
|
|
|
|
|
|
1 cos |
|
|
|
|
|
|
|
|
|
|
0; (3.74) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
a |
i 1 j 1 |
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
b |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
m n |
|
|
|
|
|
|
2i x |
|
|
|
2j 0 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
wmn |
|
|
y 0 |
Cij |
1 cos |
|
|
|
|
|
|
|
|
1 cos |
|
|
|
|
|
|
|
|
|
|
0; |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 j 1 |
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
b |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
m n |
|
|
|
|
|
|
2i x |
|
|
|
2j b |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
wmn |
|
|
y b |
Cij |
1 cos |
|
|
|
|
|
|
|
|
1 cos |
|
|
|
|
|
|
|
|
|
|
0; |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 j 1 |
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
b |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
wmn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
m n |
|
|
|
|
|
|
|
|
2j 0 |
|
|
|
|
|
|
2i x |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
y 0 |
|
|
|
|
|
Cij |
|
sin |
|
|
|
|
1 cos |
|
|
|
|
0; |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
b |
i 1 j 1 |
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
a |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
wmn |
|
|
|
|
|
|
|
2 |
m n |
|
|
|
|
|
|
|
|
2j b |
|
|
|
|
2i x |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
y b |
|
|
|
|
Cij |
|
sin |
|
|
|
1 cos |
|
|
|
|
|
|
|
|
0. |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
b |
i 1 j 1 |
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
a |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Таким образом, геометрические граничные условия на кромках |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
пластины выполняются. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Для определения коэффициентов Cij |
необходимо решить систему |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
уравнений (3.74). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
В первом приближении принимаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x |
|
2 y |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w |
|
|
C |
1 cos |
|
|
|
|
|
|
|
1 cos |
|
|
; |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
11 |
|
|
|
a |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 y |
|
|
|
|
|
|
|
(3.75) |
||
|
|
|
|
|
|
|
|
|
|
|
f1 x 1 cos |
; |
|
1 y 1 cos |
. |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|||||||
Используя (3.60), находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
a |
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fi x dx j y dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Cij |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
a |
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
fiIV x fi x dx j2 y dy 2 fi x fi x dx j y j y dy |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
fi2 x dx j y IVj |
y dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.76) |
|||
|
|
|
|
2 |
|
|
2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
где fi |
x |
sin |
; |
|
|
|
|
|
|
|
|
j y |
|
sin |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
a |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
59 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||

|
|
2 2 |
|
|
2 x |
|
|
|
2 |
2 |
|
2 y |
|||||||||||
fi |
x |
|
|
|
cos |
|
|
; |
|
j |
y |
|
|
|
|
cos |
|
|
|
; |
|
||
a |
a |
|
b |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
||||||||||
|
|
2 |
|
4 |
|
2 x |
|
|
|
2 |
4 |
|
|
2 y |
|||||||||
fiIV x |
|
|
|
|
cos |
|
|
; |
IVj |
y |
|
|
|
cos |
|
|
. |
||||||
|
a |
a |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
b |
|||||||||
Подставляя выражение производных функции в C11 и проводя интегрирование, получаем
C |
qa4 |
1 |
|
|
|
. |
|||
|
|
|
|
|
|
||||
|
|
a2 |
|
||||||
11 |
4 6D |
|
a4 |
||||||
|
|
|
3 2 |
|
|
3 |
|
|
|
|
|
b2 |
b4 |
||||||
|
|
|
|
|
|||||
(3.77)
Функция прогибов принимает вид
|
|
|
|
2 x |
|
|
|
2 y |
|
||||
|
qa4 |
|
1 cos |
|
|
1 cos |
|
|
|
||||
|
|
a |
|
b |
|
||||||||
w |
|
|
|
|
|
|
|
|
. |
||||
4 6D |
|
|
a2 |
|
|
a4 |
|
|
|||||
11 |
|
3 2 |
3 |
|
|
||||||||
|
|
|
b2 |
b4 |
|
|
|||||||
|
|
|
|
|
|
|
|
||||||
(3.78)
Максимальный прогиб в центре квадратной пластины x a2, y b2:
qa4
wmax 8 6 D .
Полученное значение совпадает с решением, полученным по методу Ритца.
3.6. Метод Канторовича-Власова
Л.В. Канторович [7] предложил метод приближенного решения задачи о минимуме двойного интеграла, что позволило двумерную задачу свести к одномерной.
В.З. Власов [8] метод Канторовича применил к решению задачи об изгибе пластин.
60
